n次元におけるEulerの不等式の初等的証明とEgan予想

今回は、自作の \(n\) 次元のEulerの不等式の初等的証明を紹介しつつ、 2023/10/18に解決された未解決問題だったEgan予想について紹介していきたいと思います。 ちなみに、初等的証明のほうは、さすがに初出だとは思いませんが、少なくとも文献は見当たりませんでした。 個人的にも、かなりエレガントな証明だと思っています。 それでは、よろしくお願いします。

2次元のEulerの不等式

まずは、基礎となる2次元でのEulerの不等式の主張と証明について考えていきます。次元を拡張しやすそうな解法の吟味もしていきたいですね。

とても有名で、美しい不等式です。2次元の場合には、様々な証明が存在します。初等的なものだけでも数種類存在し、解析的な解法も比較的計算が少なくて済みます。 例えば、こんな感じです。

• 内心と外心の距離を考える方法
• 反転を用いる方法　(だまさん(@dama_math)による解説記事)
• 六角形の面積を用いる方法　(OMC071のshoko_mathさん(@shoko_math)によるユーザー解説)
• 三角関数と有名不等式の利用　(高校数学の美しい物語さん(@mathelegant)による解説記事)
• 三角形の面積と有名不等式の利用　(高校数学の美しい物語さん(@mathelegant)による解説記事)

内心と外心の距離を考える方法

証明

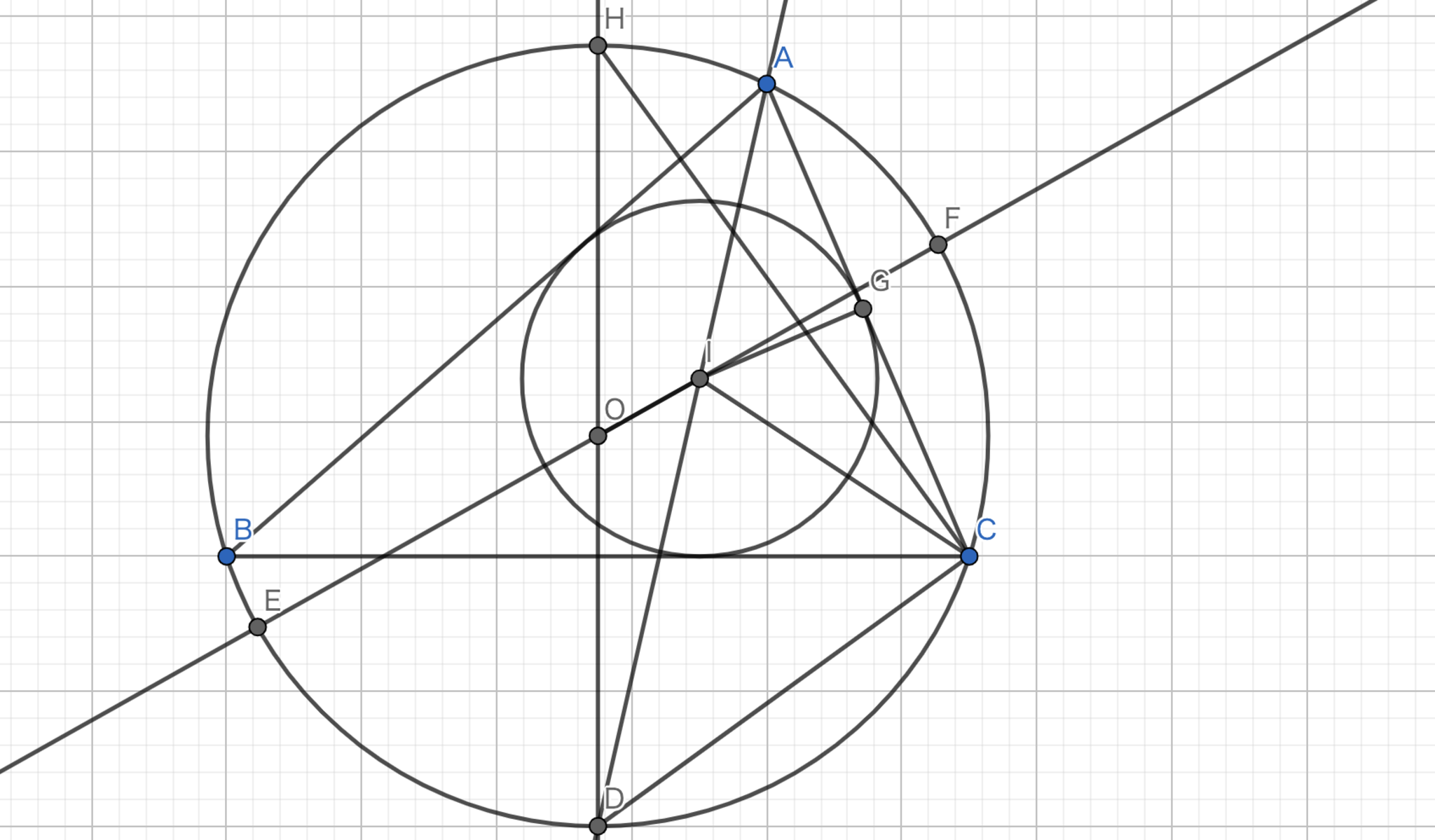
図1.Eulerの公式

方針: 方べきの定理を使用する。

　\(d^{2}=R^{2}-2Rr \Longleftrightarrow (R+d)(R-d)=2Rr\) である。 \(R+d\) は \(IE\) を表していて、 \(R-d\) は \(IF\) を表している。 方べきの定理より、\((R+d)(R-d)=|FI|\cdot |IE|=|AI|\cdot |ID|\) である。

　\(\angle{BCD} = α\) とおくと、円周角の定理より、\(\angle{BAD} = α\) となり、角の2等分線より、\(\angle{CAD} = α\) も従う。\(\angle{ACI}=β\) とすると、角の2等分線より \(\angle{BCI}=β\) である。ここで、\(\angle{ICD} = α+β\) であり、\(\angle{CID} = α+β\) であるから、三角形 \(DIC\) は2等辺三角形である。これより、\(AI \cdot ID\) = \(AI \cdot CD\) である。

　三角形 \(CDH\) と三角形 \(GIA\) はそれぞれ直角三角形であり、\(\angle{DHC} =\angle{IAG} = α\) であるから相似である。ここで三角形 \(AGI\) と三角形 \(HCD\) の相似比を \(1:k\) とすると、\(AI \cdot CD\) = \(AI \cdot GI \cdot k\) となる。また、\(AI \cdot GI \cdot k\) = \(HD \cdot GI\) である。\(HD\) = \(R\)、 \(GI\) = \(r\) であるから、\(d^{2}=R^{2}-2Rr\) である。 よって、題意は示された。\(\blacksquare\)

証明

定理2から、\(R(R-2r) = d^2 \geq 0 \) を得るから、\(R \geq 2r\) を得る。\(\blacksquare\)

内接円・外接円の半径を別の長さで表す方法

さて、上で挙げた5つの方法はどれもあまり三次元への拡張には向いていません。 強いて言えば、解析的手法ですが、これもどのみち計算量が多くなってしまいます。 ただ、不可能ではないです。既存の証明のほとんどはこの手法をとっていました。 そこで、今回は新たな方法を考えてきました。

まずは、補題を証明します。

証明

三角形の面積を \(S\)、周長を \(L\)、頂点 \(A\) の対辺の長さを \(L_A\) などとする。このとき、面積を考えることで以下を得る。 $$S=\frac{1}{2}AH_A\cdot L_{A}=\frac{1}{2}BH_B\cdot L_{B}=\frac{1}{2}CH_C\cdot L_{C}=\frac{1}{2}r\cdot L$$ これらを変形することで以下を得る。 $$\frac{1}{AH_A}=\frac{L_{A}}{2S}, \ \frac{1}{BH_B}=\frac{L_{B}}{2S}, \ \frac{1}{CH_C}=\frac{L_{C}}{2S}, \ \frac{1}{r}=\frac{L}{2S}$$ よって、 $$\frac{1}{AH_A}+\frac{1}{BH_B}+\frac{1}{CH_C}+\frac{1}{DH_D}=\frac{L_{A}+L_{B}+L_{C}}{2S}=\frac{L}{2S}=\frac{1}{r}$$ であるので題意は示された。 \(\blacksquare\)

もう一つの補題も証明します。

証明

三角形の面積を \(S\)、三角形 \(OBC\) の面積を \(S_A\) などとする。 このとき、面積比を考えることで以下を得る。(\(B,C,D\) についても同様) $$S : S-S_{A} = AO_A : AO = AO_A : R$$ これらを変形することで以下を得る。(\(B,C,D\) についても同様) $$\frac{1}{AO_A}=\frac{S-S_{A}}{SR}$$ これらを足すことで以下を得る。 $$\frac{1}{AO_A}+\frac{1}{BO_B}+\frac{1}{CO_C} = \frac{1}{SR}((S-S_{A})+(S-S_{B})+(S-S_{C}))=\frac{2S}{SR}=\frac{2}{R}$$ であるので題意は示された。 \(\blacksquare\)

証明

補題1、補題2から示すべき命題は以下と同値であることがわかる。 $$\frac{1}{AO_A}+\frac{1}{BO_B}+\frac{1}{CO_C} \le \frac{1}{AH_A}+\frac{1}{BH_B}+\frac{1}{CH_C}$$ \(\frac{1}{AO_A} \le \frac{1}{AH_A} \iff AH_A \le AO_A\) であり、\(AH_A\) は点 \(A\) から直線 \(BC\) への最短距離であるから、この不等式は成立する。 よって、目的の式も正しいことがわかる。 \(\blacksquare\)

示すことができました。実は、この証明は次元にほとんど依存しないのです！この方針ならば簡単に次元を拡張できそうですね！ということで、次は3次元に拡張していきます。

\(n\) 次元のEulerの不等式

仕上げです。高次元の初等幾何のお話がちゃんと載っている資料が全然なくて、この表記とか議論が正しいのかは全然自信ないです。 ただ、拡張するとこうなるはずです。

三次元に関しては、動画を作成しています。もしよかったら見てみてください。

\(n\) 次元への拡張の話では、単体とか、超球などの聞きなれない言葉が登場するかもしれませんが、これらは四面体や球などの拡張の概念です。

内接\(n\) 次元超球・外接\(n\) 次元超球の半径を別の長さで表す方法

証明

\(n\) 次元単体の超体積を \(V\)、超面積(?)を \(S\)、頂点 \(X_1\) の向かいの\(n-1\) 次元単体の超面積(?)を \(S_1\) などとする。このとき、超体積を考えることで以下を得る。 $$V=\frac{1}{n}X_1H_1\cdot S_{1}=\frac{1}{n}X_2H_2\cdot S_{2}=\cdots =\frac{1}{n}X_{n+1}H_{n+1}\cdot S_{n+1} = \frac{1}{n}r\cdot S$$ これらを変形することで以下を得る。 $$\frac{1}{X_1H_1}=\frac{S_{1}}{nV}, \ \frac{1}{X_2H_2}=\frac{S_{2}}{nV},\cdots , \ \frac{1}{X_{n+1}H_{n+1}}=\frac{S_{n+1}}{nV}, \ \frac{1}{r}=\frac{S}{nV}$$ よって、 $$\frac{1}{X_1H_1}+\frac{1}{X_2H_2}+\cdots +\frac{1}{X_{n+1}H_{n+1}}=\frac{S_{1}+S_{2}+\cdots +S_{n+1}}{nV}=\frac{S}{nV}=\frac{1}{r}$$ であるので題意は示された。 \(\blacksquare\)

もう一つの補題も証明します。

証明

\(n\) 次元単体の超体積を \(V\)、\(n-1\) 次元単体 \(OX_2X_3\cdots X_{n+1}\) の超体積を \(V_1\) などとする。 このとき、超体積比を考えることで以下を得る。(\(X_2,X_3,\cdots ,X_{n+1}\) についても同様) $$V : V-V_{1} = X_1O_1 : X_1O = X_1O_1 : R$$ これらを変形することで以下を得る。(\(X_2,X_3,\cdots ,X_{n+1}\) についても同様) $$\frac{1}{X_1O_1}=\frac{V-V_{1}}{VR}$$ これらを足すことで以下を得る。 $$\frac{1}{X_1O_1}+\frac{1}{X_2O_2}+\cdots +\frac{1}{X_{n+1}O_{n+1}} = \frac{1}{VR}((V-V_{1})+(V-V_{2})+\cdots +(V-V_{n+1}))=\frac{nV}{VR}=\frac{n}{R}$$ であるので題意は示された。 \(\blacksquare\)

証明

補題3、補題4から示すべき命題は以下と同値であることがわかる。 $$\frac{1}{X_1O_1}+\frac{1}{X_2O_2}+\cdots +\frac{1}{X_{n+1}O_{n+1}} \le \frac{1}{X_1H_1}+\frac{1}{X_2H_2}+\cdots +\frac{1}{X_{n+1}H_{n+1}}$$ \(\frac{1}{X_1O_1} \le \frac{1}{X_1H_1} \iff X_1H_1 \le X_1O_1\) であり、\(X_1H_1\) は点 \(X_1\) から \(n-1\) 次元単体 \(X_2X_3\cdots X_{n+1}\) への最短距離であるから、この不等式は成立する。 よって、目的の式も正しいことがわかる。 \(\blacksquare\)

目標達成！お疲れさまでした。

Egan予想

ここで終わっても良いのですが、タイムリーなことに2023/10/18にEgan予想というものが肯定的に解決されました。 Egan予想とは、端的に言えばEulerの公式(定理2)の\(n\) 次元への拡張です。とりあえず、以下にEgan予想の主張を載せてみたいと思います。 (Eganさんは予想しただけであって、証明はしていません。)

原論文はこちらになります。贅沢な使い方ですが、こちらの系として今回の不等式を示すことができます。

それはさておき、実は、このEgan予想のEganさんは驚くべきことに数学者というわけではないのです(数学科は卒業しているみたいです)。 彼は、めちゃくちゃ科学的にリアルなSFを書く作家だそうで(wiki調べ)、様々な賞も受賞しているようです。 今回解決された論文を少しだけ除いてみると、計算をメインにやっていることが伺えます。 私には、これを追うことのできる数学力はありませんが、どうもかなり対称的で綺麗な計算になっているように思えます。 ということで、ちょっとしたお話でした！

参考文献

[1] だま氏：円の反転とオイラーの不等式 , 数学徘徊記 , https://su-hai.hatenablog.com/entry/6264546

[2] shoko_math：OMC071(F) ユーザー解説 , Online Math Contest , https://onlinemathcontest.com/contests/omc071/editorial/1929/21

[3] マスオ：オイラーの定理（内心と外心の距離）とオイラーの不等式の証明を3通りずつ , 高校数学の美しい物語 , https://manabitimes.jp/math/580

[4] Sergei Drozdov：Egan conjecture holds , arXiv , https://export.arxiv.org/abs/2310.10816