四円と相似中心
今回は、基本的な証明問題を解いてみたいと思います。それでは、よろしくお願いします。
問題
問題: 四円と相似中心
互いに共有点を持たない四円 \(\omega_1,\omega_2,\omega_3,\omega_4\) が存在する。 点 \(O_{ij}\) を円 \(\omega_i,\omega_j\) の共通外接線の交点とする。 \(O_{12}O_{34},O_{23}O_{41},O_{13}O_{24}\) の中点をそれぞれ \(P,Q,R\) とするとき、これらは共線となることを示せ。
使う道具は難しいですが、基本的な問題です。
解説
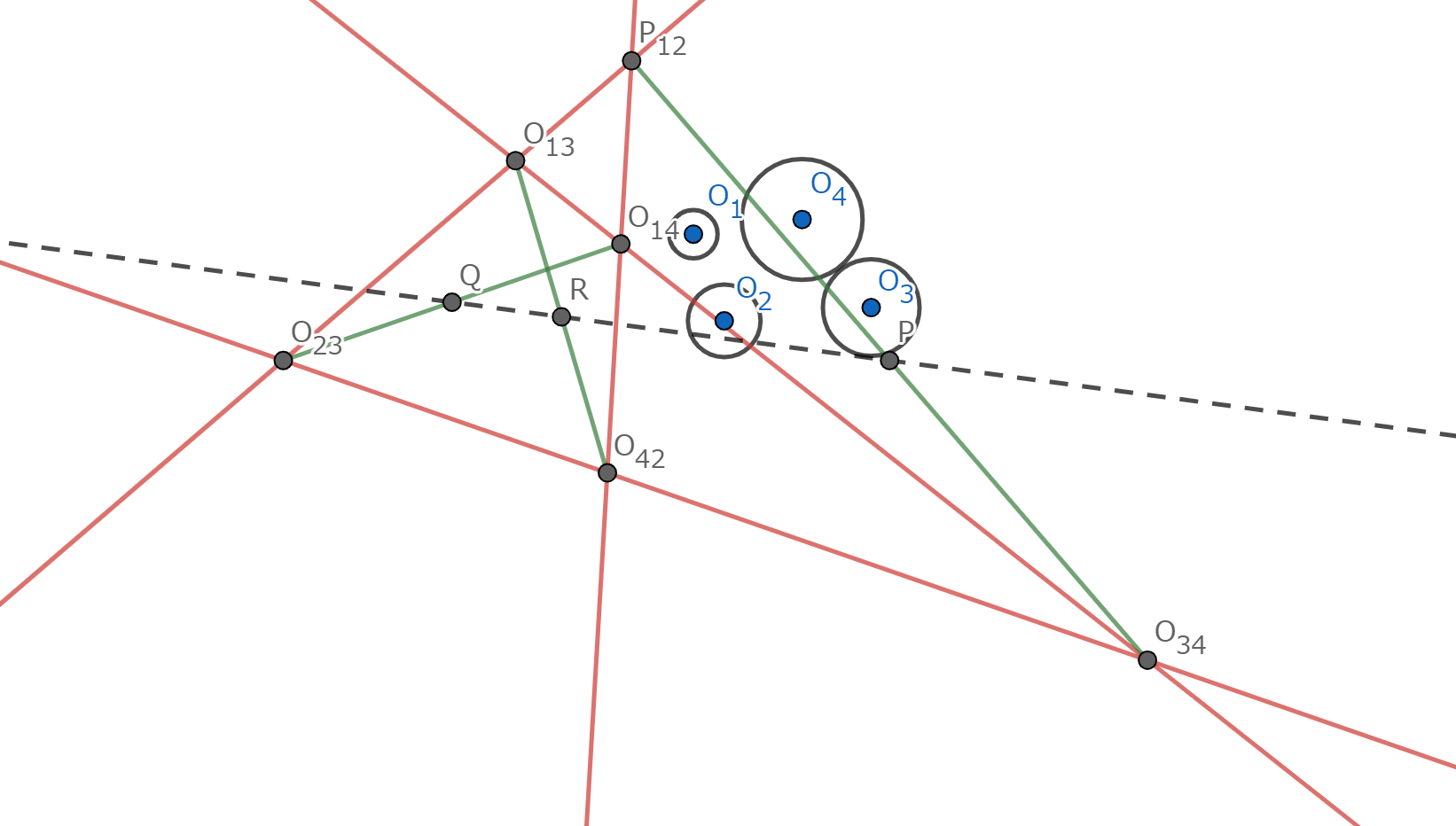
図1.解説の図形
Mongeの定理より、六点 \(O_{12},O_{23},O_{34},O_{41},O_{13},O_{24}\) はどの三点を選んでも共線となるような四角形(完全四角形)である。 よって、完全四角形の三本の対角線の中点が共線であることを示せばよい。ここで、二頂点を無限遠点へ飛ばすような適切な射影変換を考えれば、それらの中点は自明に共線である。 \(\blacksquare\)
この完全四角形における共線は、ニュートン線と呼ばれているようです。射影変換ではなく、座標などでも容易に示すことができます。