60°と正三角形
今回は、基本的な証明問題を解いてみたいと思います。それでは、よろしくお願いします。
問題
問題: 60°と正三角形
\(|AC|>|AB|\) , \(\angle{A}=60°\) なる不等辺三角形 \(ABC\) において、その外接円を \(\Omega\) とし、\(\Omega\) と \(BC\) の垂直二等分線の交点のうち、\(A\) を含む側の交点を \(D\) とする。 \(AD\) の垂直二等分線と \(AC\) の交点を \(E\) とするとき、\(|AB|=|CE|\) となることを示せ。
基本的な問題になっています。
解説
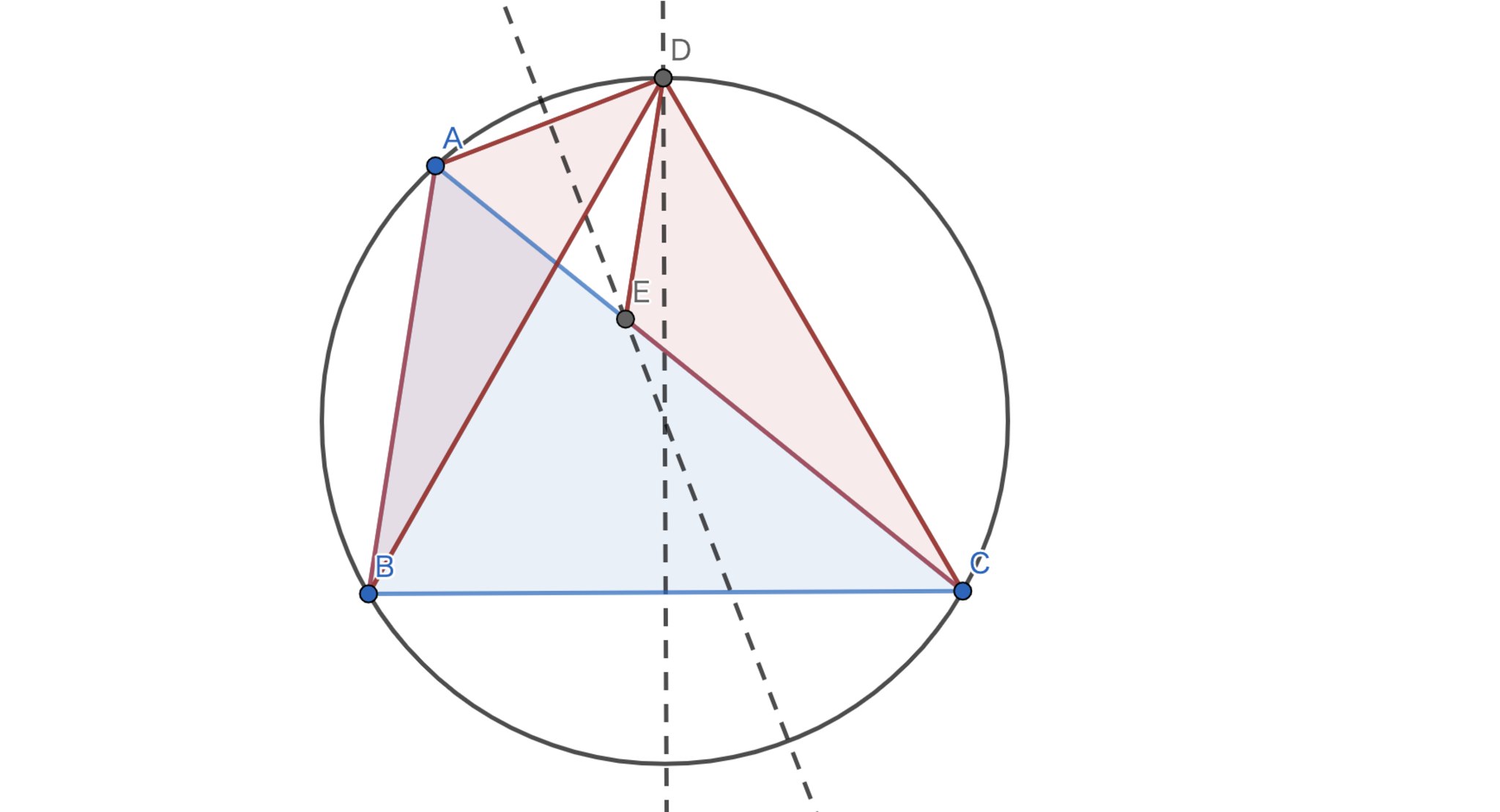
図1.解説の図形
三角形 \(DBC,EAD\) は共に正三角形なので \(AD=DE,DB=DC\) となる。 また、\(\angle{A}=\angle{D}=60°\) となるので \(\triangle{DAB} \equiv \triangle{DEC}\) を得るから \(AB=EC\) である。