反転による命題の変換
今回は、反転一発ゲーを解いていきます。なぜ反転を使いたくなるのかを言語化して解いてみましょう。それでは、よろしくお願いします。
問題
三角形 \(ABC\) の外心を \(O\) とする。 \(OA,OB,OC\) を直径とする円をそれぞれ \(\omega_1,\omega_2,\omega_3\) とし、\(OBC,OCA,OAB\) の外接円をそれぞれ \(\Gamma_1, \Gamma_2, \Gamma_3\) とする。 \(\omega_1\) と \(\Gamma_1\) の交点を \(P_{1}\) とし、同様に \(P_2,P_3\) についても定めたとき、\(O,P_1,P_2,P_3\) は同一円周上に存在することを示せ。
反転についての知識がない方は、こちらを参照することをお勧めします。
解説
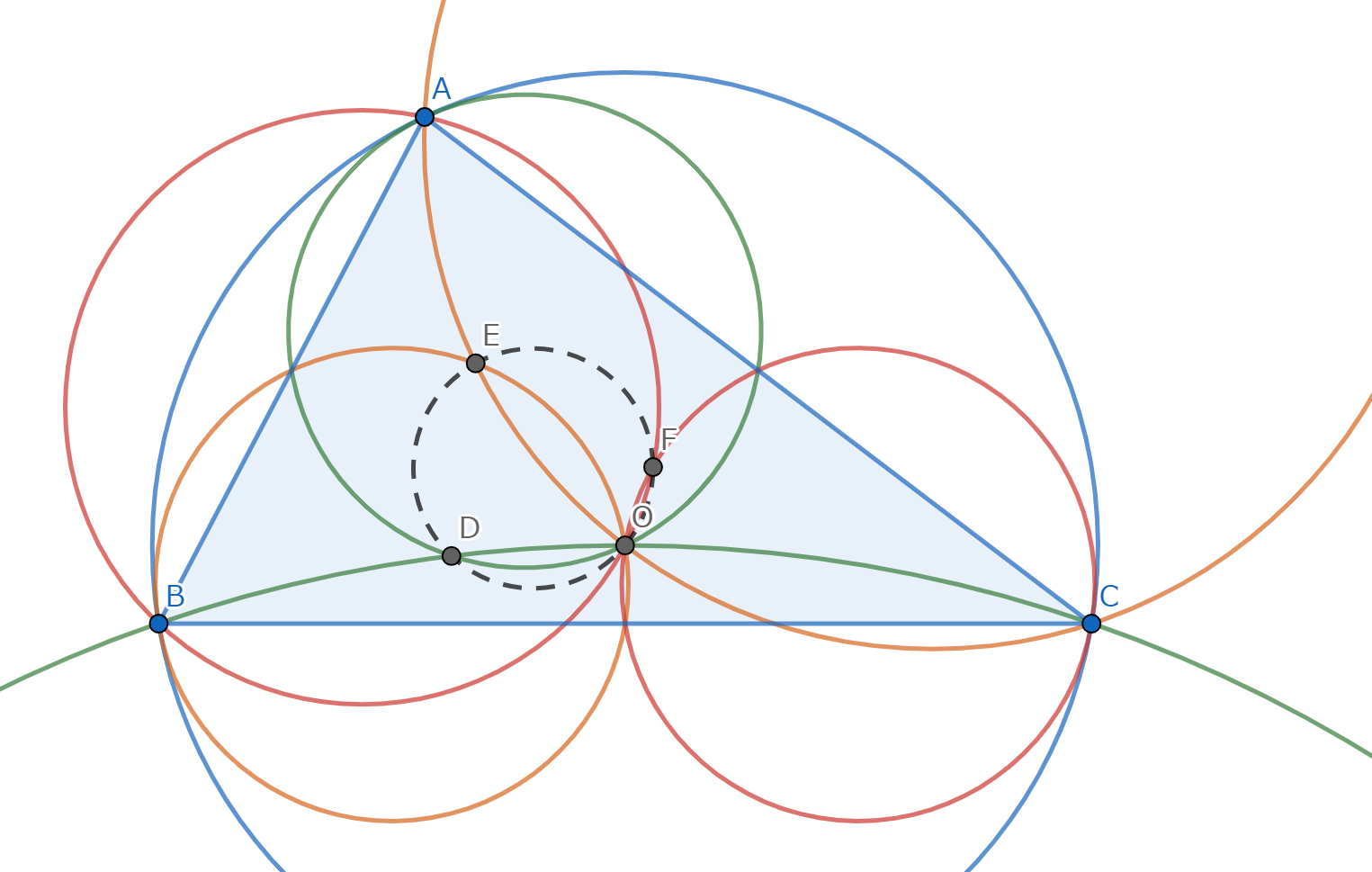
図1.問題文の図形
\(ABC\) の外接円での反転を考える。\(X\) を反転したものを \(X'\) と表現する。 このとき、示すべきことは \(P_1',P_2',P_3'\) の共線である。 \(\Gamma_1, \Gamma_2, \Gamma_3\) はそれぞれ反転によって \(BC,CA,AB\) に移る。 \(\omega_1,\omega_2,\omega_3\) はそれぞれ反転によって \(A,B,C\) に関する外接円の接線へと移る。 \(\omega_1,\omega_2\) の交点の反転先を \(M_1\) などとすれば、\(M_1C,M_2A,M_3B\) は全て三角形 \(ABC\) のSymmedian Pointを通る。 したがって、\(P_1',P_2',P_3'\) はDesarguesの定理より共線であるから題意は示された。 \(\blacksquare\)
なぜ反転が有効か?
今回の問題では、複数の円が同じ点(外心)を通っているため外心を中心とする円で反転すると円が直線に変わり状況がシンプルになります。 他にも反転は円同士が接することの証明などに有効です。今回はあまりにも露骨でしたが、少しでも反転が刺さる可能性を感じたら、試してみましょう。