Ravi変換と幾何的に見る不等式

今回は、典型的な \(\tan\) 置換の不等式を敢えて幾何的に解いていきたいと思います。実用的ではないかもしれませんが楽しんでいただけたらなと思います。

問題

もちろん、\(\tan\) の置換でも解くことができます。むしろ、そちらを推奨します。

解説

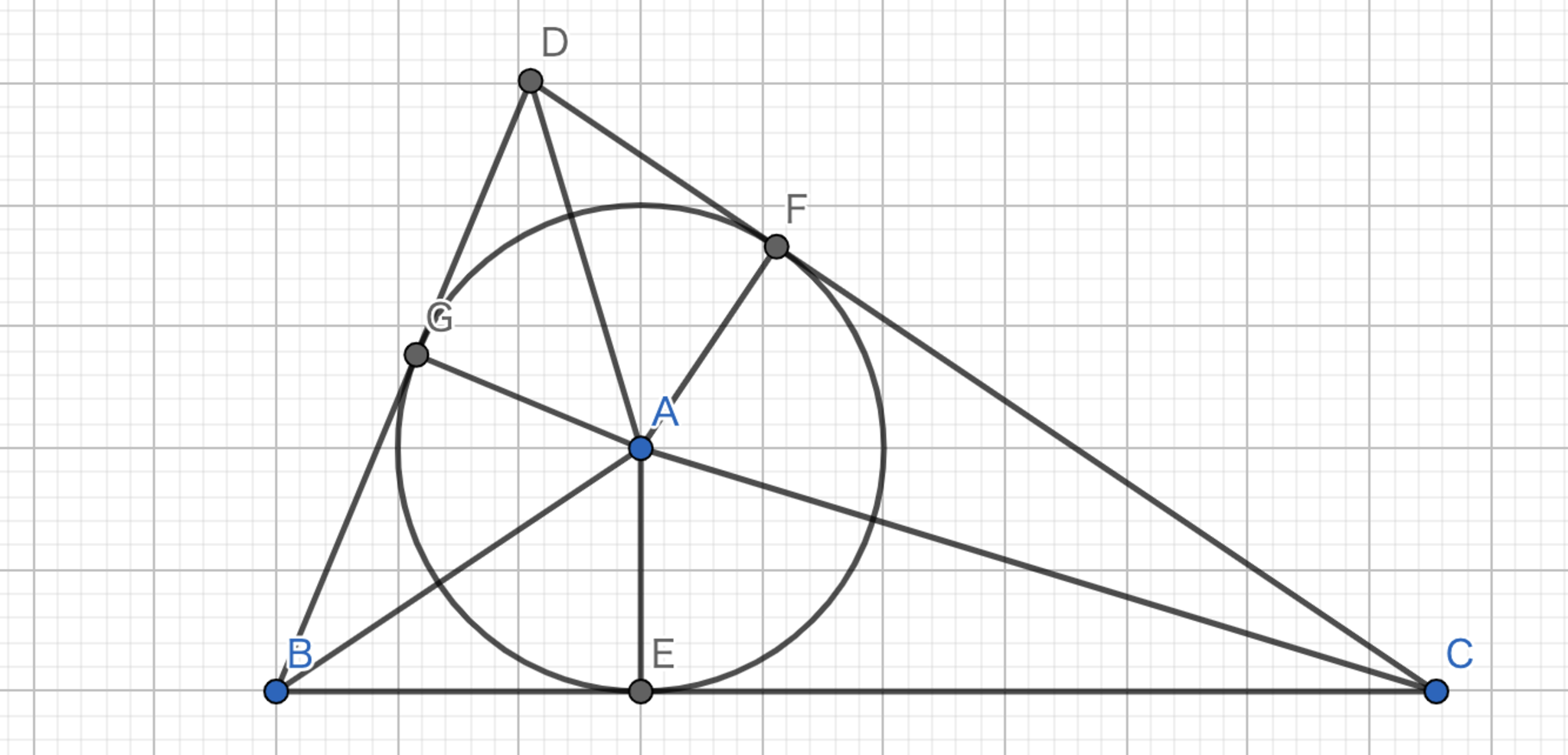
図1.問題文の図形

上の図において,\(|BE|=a, |CF|=b, |DG|=c\) とする。このときの三角形の成立条件は \(a,b,c\) が正と同値である。 また、三角形 \(DBC\) の内接円の半径は \(\sqrt{\frac{abc}{a+b+c}}\) であり \(a+b+c=abc\) より内接円の半径は \(1\) となる。 したがって、\(|AB|=\sqrt{a^{2}+1}\) , \(|AC|=\sqrt{b^{2}+1}\) , \(|AD|=\sqrt{c^{2}+1}\) となる。 このとき、\(X=\angle\mathrm{ABE}\) , \(Y=\angle\mathrm{ACF}\) , \(Z=\angle\mathrm{ADG}\) とすると、不等式の左辺は \(\cos X+\cos Y+\cos Z\) となる。 ここで、\(X+Y+Z=\frac{\pi}{2}\) であることに注意せよ。 \(cos \theta\) は \(0 < \theta < \frac{\pi}{2}\) では上に凸なので \[\cos X+\cos Y+\cos Z\le3\cos\left(\frac{X+Y+Z}{3}\right)\ =3\cos\frac{\pi}{6}=\frac{3\sqrt{3}}{2}\] であり。したがって、 \[ \frac{a}{\sqrt{a^{2}+1}}+\frac{b}{\sqrt{b^{2}+1}}+\frac{c}{\sqrt{c^{2}+1}}\le\frac{3\sqrt{3}}{2} \] が得られて題意は示された。

(内接円の半径が \(\sqrt{\frac{abc}{a+b+c}}\) と表されることに行間を感じる方は こちら を見てみると良いかもしれません。)

まとめ

もう一度言います。これは実用的ではありません。あくまで観賞用として楽しんでいただけたらなと思います。

・\(a+b+c=abc\) という条件を見たらtanによる置換を考えるのはマジで大事です。本解はこっちです。

・Ravi変換の公式は覚えておくと便利なことがあります。

・AM-GMやJensen等の有名不等式を用いると良いでしょう。