三平方の定理で幾何的に見る不等式
今回は、珍しいタイプの整数の不等式を解いていきます。普通に難しいです。
問題
\(k\) を正整数とする。このとき、以下の不等式を示せ。 \[\sum_{n=1}^{6k}\sqrt{1+n^{2}}>\sum_{n=1}^{3k}\sqrt{4+\left(4n-1\right)^{2}}>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}}\]
計算で攻略すると、かなり大変になります。数式の意味を考察してみると良いかもしれません。
解説
解法1(展開して計算)
左辺 > 中辺 が成り立つことは \[ \begin{align} \sum_{n=1}^{3k}\left(\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}\right)>\sum_{n=1}^{3k}\sqrt{\left(4n-1\right)^{2}+4} \end{align} \] が成り立つことと同値である。したがって、 \[ \sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}>\sqrt{\left(4n-1\right)^{2}+4} \] を示せば十分である。これを整理することで、 \[ \begin{align} 16n^{4}-16n^{3}+12n^{2}-4n+2>16n^{4}-16n^{3}+12n^{2}-4n+1 \\ \end{align} \] を得るので、左辺 > 中辺 が示された。
中辺 > 右辺が成り立つことは \[ \begin{align} \sum_{n=1}^{k}\left(\sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}\right)>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}} \end{align} \] が成り立つことと同値である。したがって、 \[ \sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}>\sqrt{36+\left(36n-15\right)^{2}} \] を示せば十分である。これを整理することで、 \[ \begin{align} 144^{2}n^{4}-240\cdot144n^{3}+126\cdot144n^{2}-120\cdot26n+425>144^{2}n^{4}-240\cdot144n^{3}+126\cdot144n^{2}-120\cdot26n+169\\ \end{align} \] を得るので、中辺 > 右辺 が示された。 これより、左辺 > 中辺 > 右辺 が示された。
(この解答は翁さん (@I_______nu)によるものです。ありがとうございます。)
解法2(幾何的に計算)
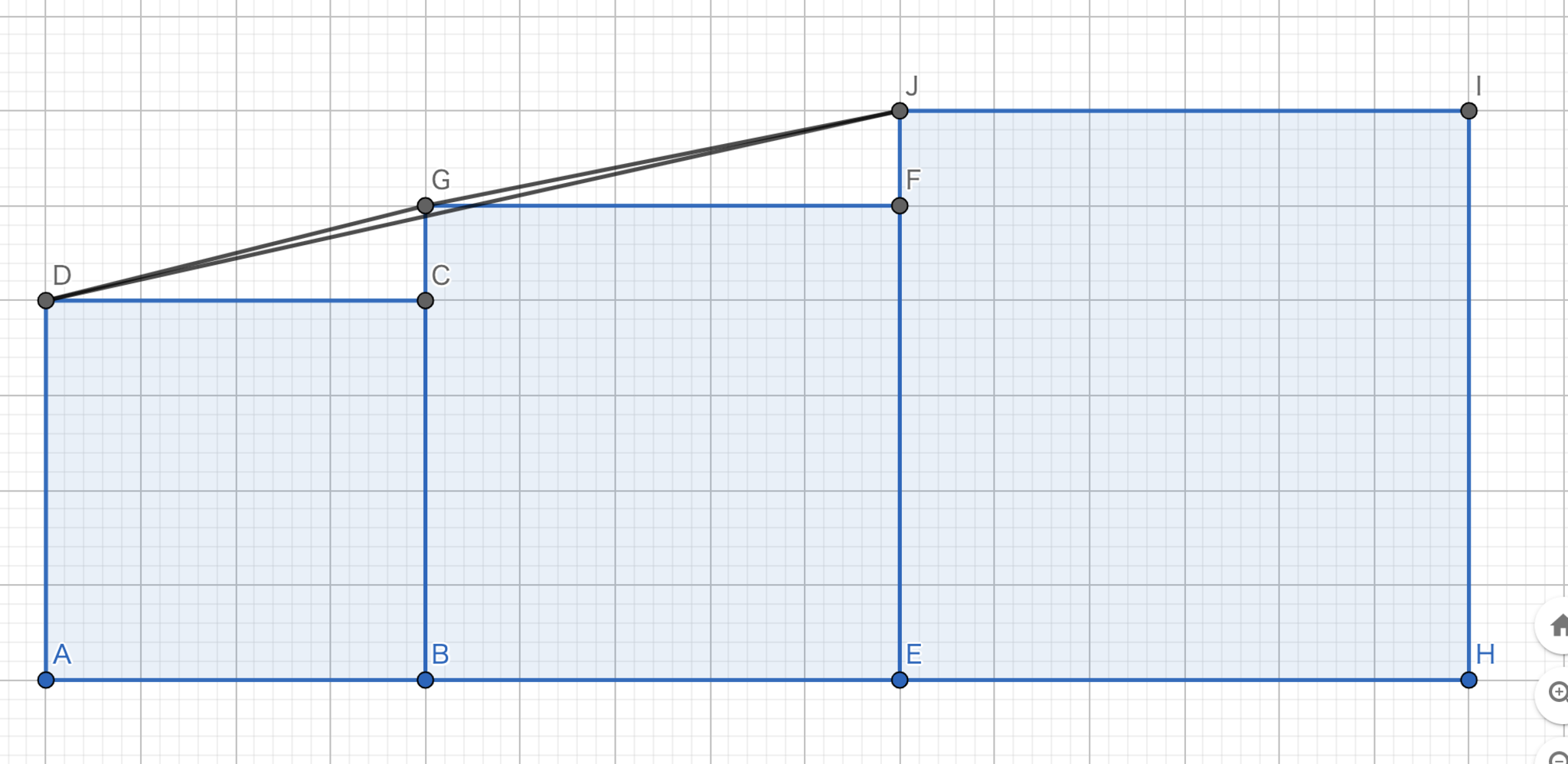
図1.左辺 > 中辺 の図
左辺 > 中辺 が成り立つことは \[ \begin{align} \sum_{n=1}^{3k}\left(\sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}\right)>\sum_{n=1}^{3k}\sqrt{\left(4n-1\right)^{2}+4} \end{align} \] が成り立つことと同値である。したがって、 \[ \sqrt{\left(2n-1\right)^{2}+1}+\sqrt{\left(2n\right)^{2}+1}>\sqrt{\left(4n-1\right)^{2}+4} \] を示せば十分である。 図1において、\(|AB|=2n-1,|BE|=2n\) とすると \[|DG|=\sqrt{\left(2n-1\right)^{2}+1}, \ |GJ|=\sqrt{\left(2n\right)^{2}+1}, \ |DJ|=\sqrt{\left(4n-1\right)^{2}+4}\] となる。三角不等式より、\(|DG|+|GJ| > |DJ|\) であるから 左辺 > 中辺 は示された。
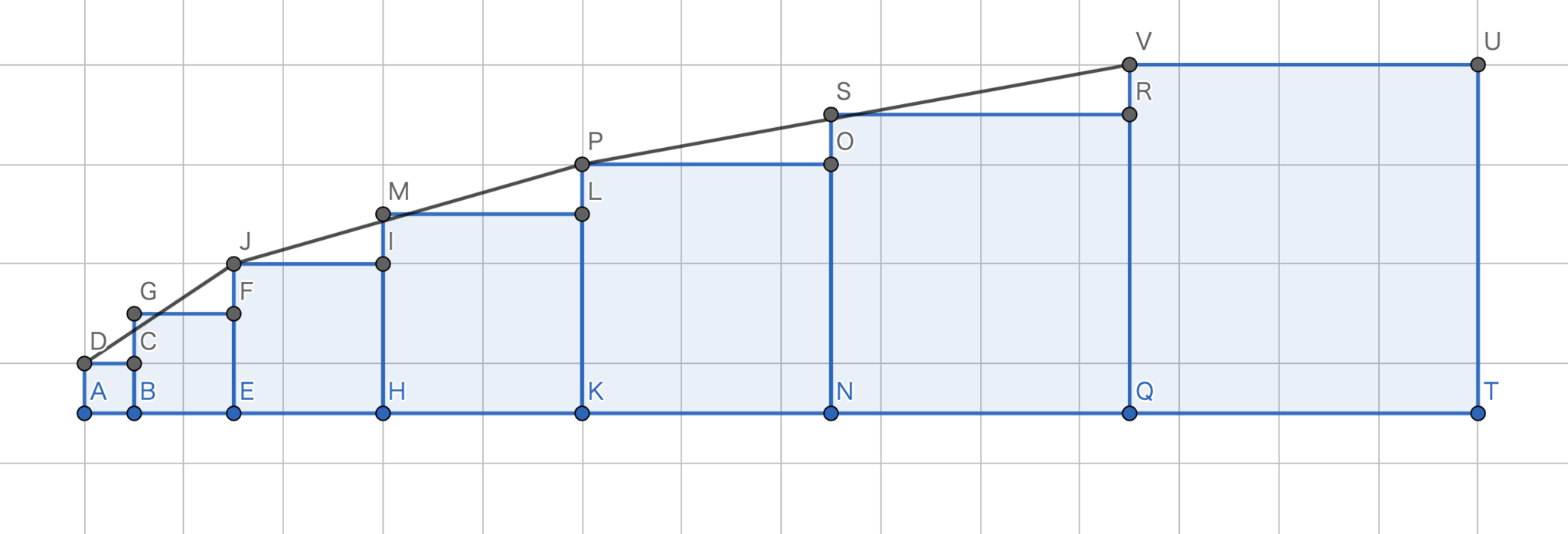
図2.中辺 > 右辺 の図
中辺 > 右辺が成り立つことは \[ \sum_{n=1}^{k}\left(\sqrt{\left(4\left(3n-2\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n-1\right)-1\right)^{2}+4}+\sqrt{\left(4\left(3n\right)-1\right)^{2}+4}\right)>\sum_{n=1}^{k}\sqrt{36+\left(36n-15\right)^{2}} \] が成り立つことと同値である.したがって、 \[\sqrt{\left(12n-9\right)^{2}+4}+\sqrt{\left(12n-5\right)^{2}+4}+\sqrt{\left(12n-1\right)^{2}+4}>3\sqrt{\left(12n-5\right)^{2}+4}\] を示せば十分である。図11においても 左辺 > 右辺 の証明と同様に考えると \[(中辺)=|DG|+|GJ|+|JM|+|MP|+|PS|+|SV| , \ (右辺)=|DV|\] となって、三角不等式より 中辺 > 右辺 が示された。 したがって、題意は示された。
まとめ
この問題は半分本気、半分観賞用です。「こういう考え方もあるのか~」と思っていただければ嬉しいです。
・三平方の定理は稀に刺さる事があります。二乗和+平方根 ときたらちょっとだけ思い出してやってください。
・もっともよく出るのは、三平方の定理ではなく角度が \(60^{\circ}\) の余弦定理などです。\(a^2+ab+b^2\) の形ですね。