外心、ナーゲル点、垂心の内心に関する対称点の共線
今回は、とてもおもしろい主張について紹介していきます。 ついでに、ナーゲル線の初等的証明も添えておきます。 今回の問題には、エブリバーガーくんと二人で取り組みました。 それでは、よろしくお願いします。
主張
三角形 \(ABC\) において、ナーゲル点、外心、内心に関する垂心の対称点は共線であり、特に外心は残りの二点の中点である。
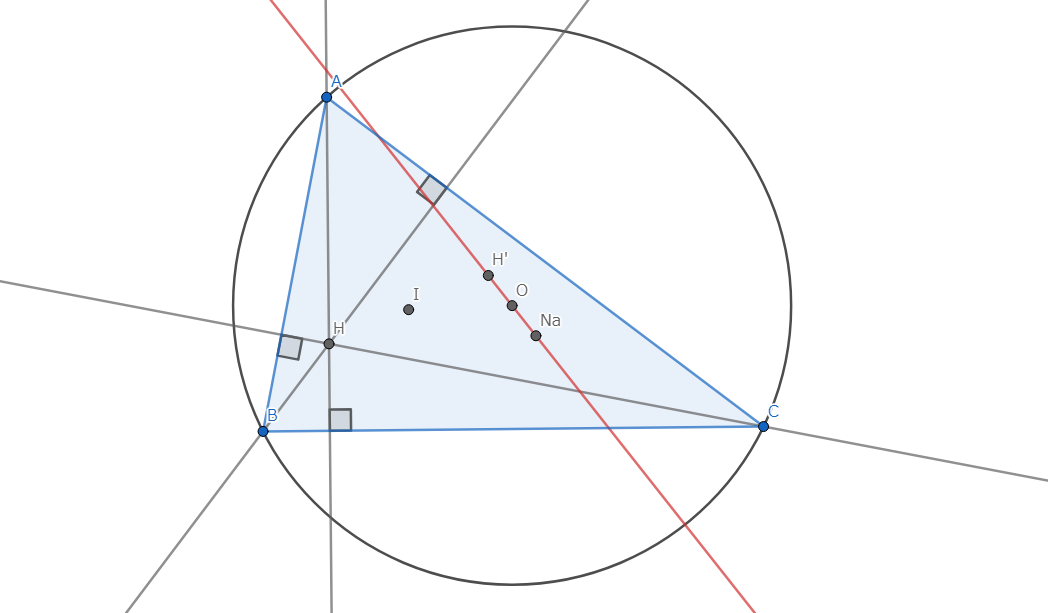
図1.命題1 -主張
ナーゲル点とは、傍心版のジュルゴンヌ点です。つまり、三角形 \(ABC\) において、各辺と傍接円の接点を \(X,Y,Z\) としたときの、\(AX,BY,CZ\) の共点をナーゲル点と呼びます。
今回は、この命題を二通りの方法で解いていきます。
証明
それでは証明をしていきます。オイラー線とナーゲル線を用いた証明です。
正三角形でない任意の三角形に対して外心、重心、垂心は共線であり、特に、\(HG:GO = 2:1\) である。
証明
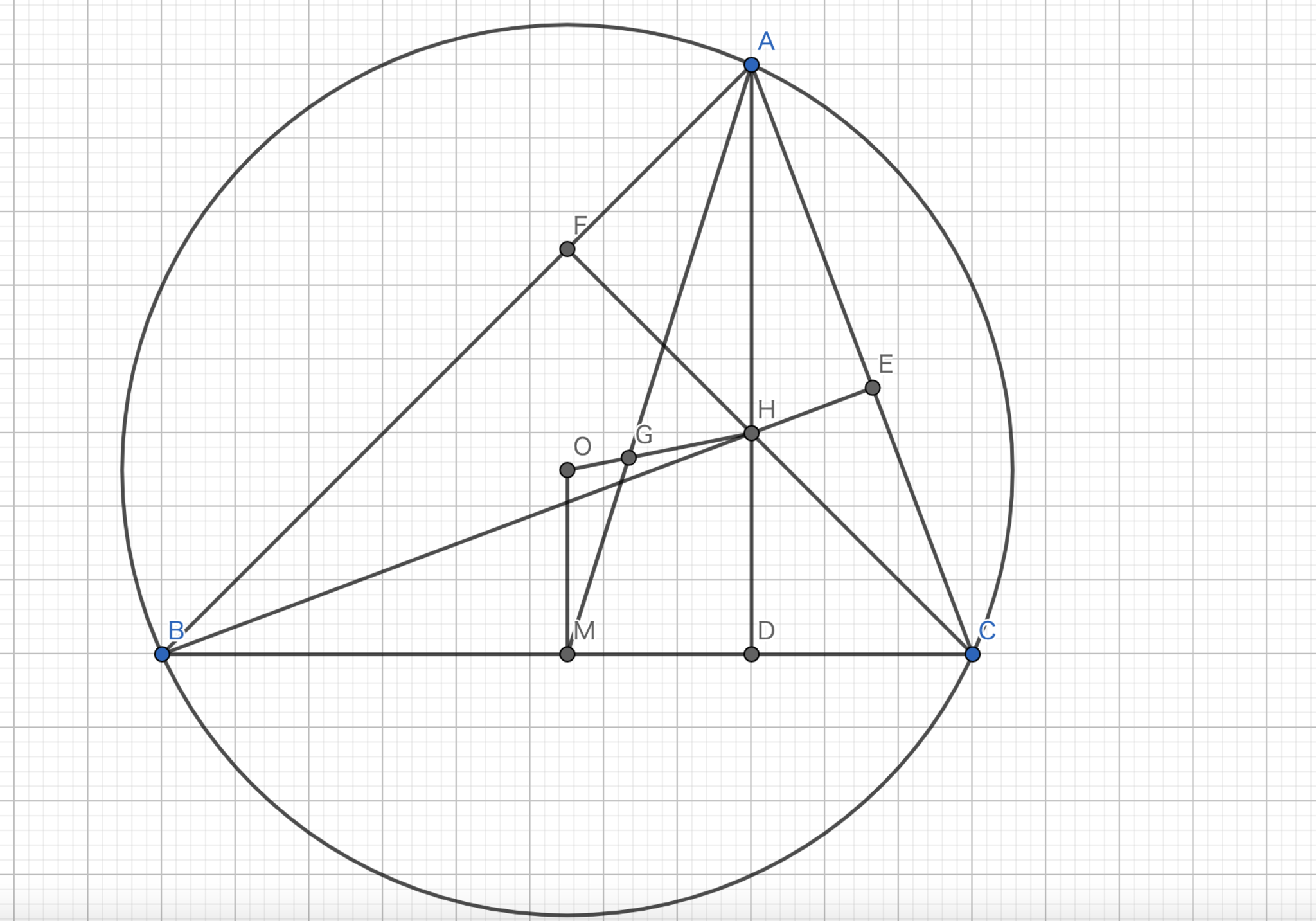
図2.補題1-証明
直線\(CO\)と円との交点を\(P\)とする。
このとき、\(CP\)は円の直径である。
また、\(BC\)の中点を\(M\)とすると、中点連結定理より、\(OM\) は \(PB\) に平行であり、\(2|OM|=|PB|\)である。
\(AD \perp BC\)、\(PB \perp BC\) であるから、\(AD \parallel PB\) である。
また、垂心の性質と円周角の定理より、\(BE \perp AC\)、\(PA \perp AC\) であるから、\(BE \parallel PA\) である。
よって、四角形\(PBHA\)は平行四辺形である。
よって、\( |AH| = |PB| = 2|OM| \)。
図において、三角形\(AGH\) と三角形\(MGO\) は、\( \angle MGO = \angle AGH\)、\( \angle GAH = \angle GMO (\because AD \parallel OM) \) であるから、相似である。
さらに、\( |AH| = 2|OM| \) より、その相似比は \(2:1\) である。
また、\(G\) は \(AM\) を \(2:1\) に内分する点であり、\(M\) が中点であるから、\(G\) は重心である。
これより、三点\(O,G,H\)は一直線上に並び、\( |OG|:|GH| = 1:2 \) である。
\(\blacksquare\)
三角形 \(ABC\) において、ナーゲル点 \(Na\)、内心 \(I\)、重心 \(G\) は共線であり、特に、 \(NaG : GI = 2:1\) である。
証明
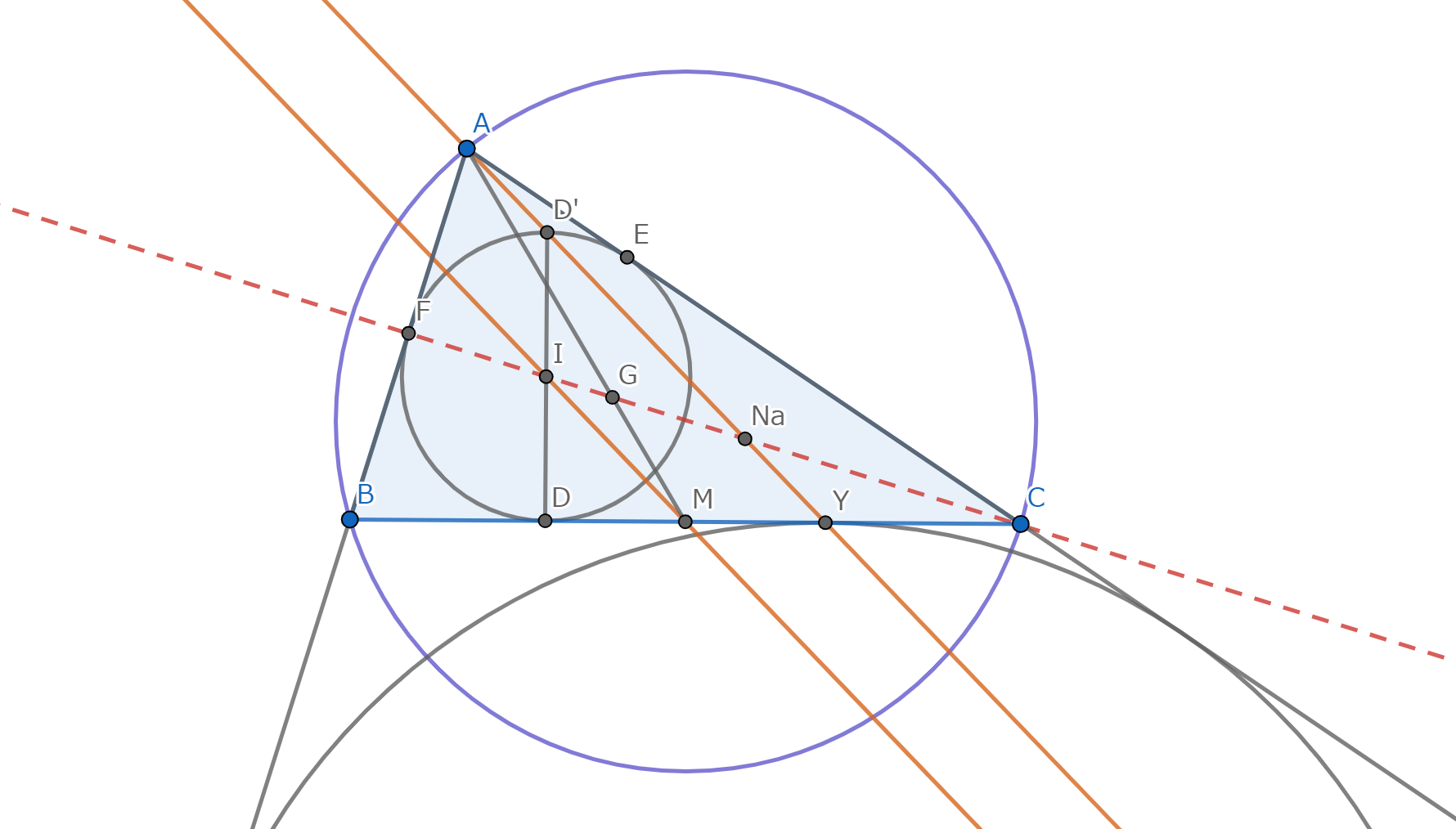
図3.補題2 -証明
図のように、点を命名する。内心、傍心にまつわる構図から、\(M\) は \(DY\) の中点である。 よって、三角形 \(D'DY\) に関する中点連結定理から、\(IM // D'Y\) であり、\(IM:D'Y = 1:2\) である。 三角形 \(IMG, \ NaGA\) の相似を示す。 平行から、\(\angle{IMG} = \angle{NaAG}\) であり、\(AG:MG = 2:1\) である。 内心、傍心にまつわる構図から \(D'Y = ANa\) であるので、\(IM:D'Y = 1:2\) と併せて、\(IM : NaA = 1:2\) を得る。 このことから、目標の相似が得られた。 よって、\(\angle{IGM} = \angle{NaGA}\) であるので、三点 \(Na,I,G\) は共線であり、さらに \(NaG : GI = 2:1\) である。 \(\blacksquare\)
補題1と補題2を使って、証明をしていきます。 ナーゲル点や、垂心の内心に関する対称点など見慣れない点が多いと思いますが、補題2を踏まえれば、自然かもしれません。
三角形 \(ABC\) において、ナーゲル点、外心、内心に関する垂心の対称点は共線であり、特に外心は残りの二点の中点である。
証明
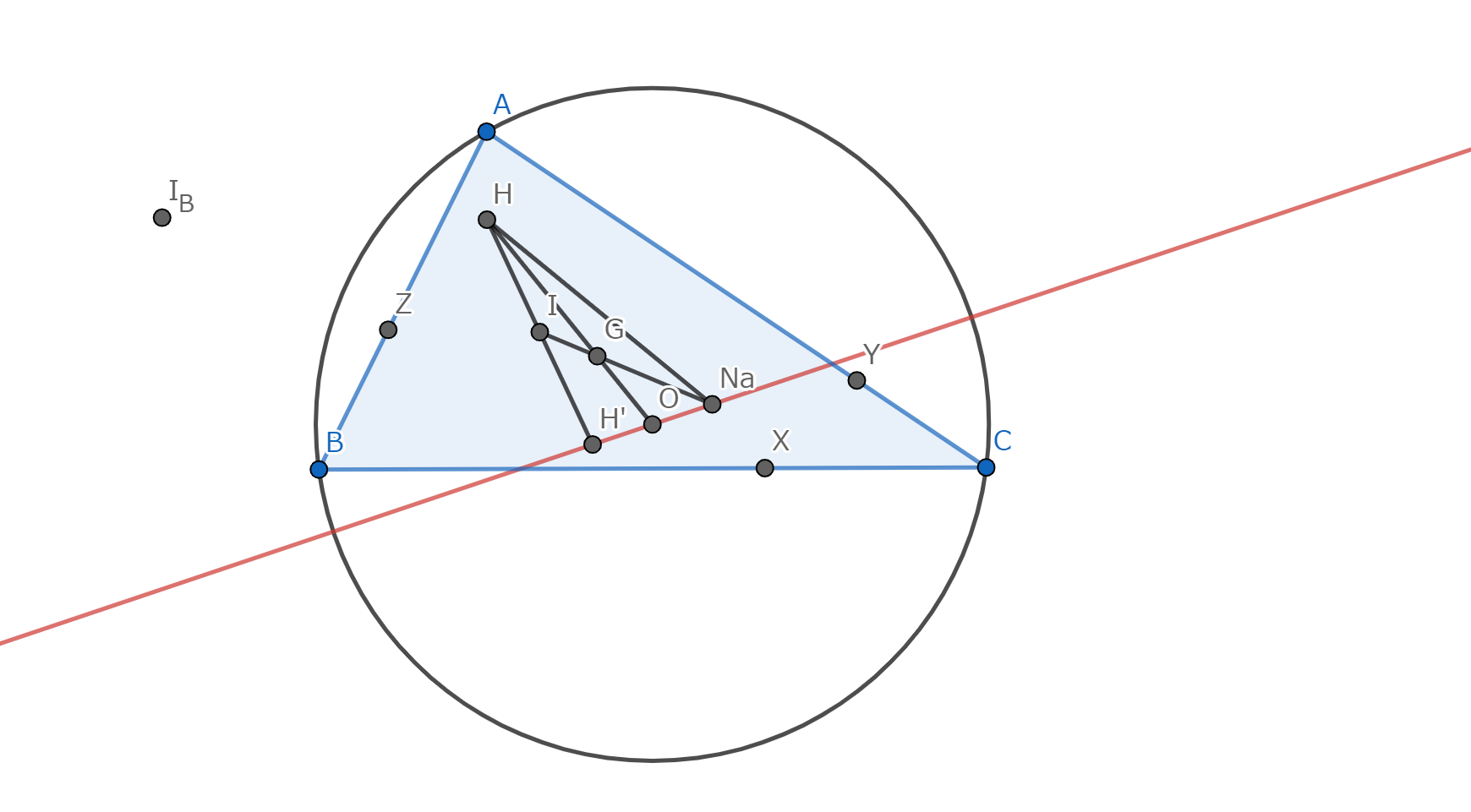
図4.命題1 -証明
図のように点に名前を付ける。 補助定理1から、\(NaG:GI=2:1\) であり、点 \(I\) は \(HH'\) の中点であるから、点 \(G\) は三角形 \(HH'Na\) の重心である。 さらに、補題1から、\(HG:GO = 2:1\) であるから、\(O\) は \(H'Na\) の中点である。よって、題意は示された。\(\blacksquare\)