難角問題の解き方
今回は予選で頻出な難角問題について、ある程度太刀打ちできるようになったので思考方法を言語化してみます。 僕は難角問題初心者なので至らない部分も多いと思いますが、よろしくお願いします。
本記事の作成にあたって、@tyenn7さんには大変お世話になりました。ありがとうございます!
心構え
難角問題はただ与えられた角度を使って、別の角度を計算するといった方法では100%解けません。 解けたら、難角問題ではないです。 そこで意識してほしいのが、「隠れた特殊性を見つける」ということです。 以下では、それを達成するための典型的な手法を紹介していきます。
等しい長さを貼り付ける
等しい長さを見たら、とりあえず貼り付けておくとよいかもしれません。まずは、 中学受験でも頻出の問題で見てみましょう。
正方形 \(ABCD\) の辺 \(CD,DA\) 上に点 \(E,F\) が存在して \(\angle{EBF=45°},\angle{DFE}=32°\) を満たすとき \(\angle{BEC}\) の大きさを求めよ。
\(45°\) という条件が \(90°\) と関連していることに気付けると一気に進みます。
解答
\(EC=E'A\) なる点を図のように取る。 \(\triangle{BE'F} \equiv \triangle{BEF}\) であるので \(\angle{FEB}=\angle{CEB}\) が得られて \(\angle{BEC}=\boxed{61°}\) となる。
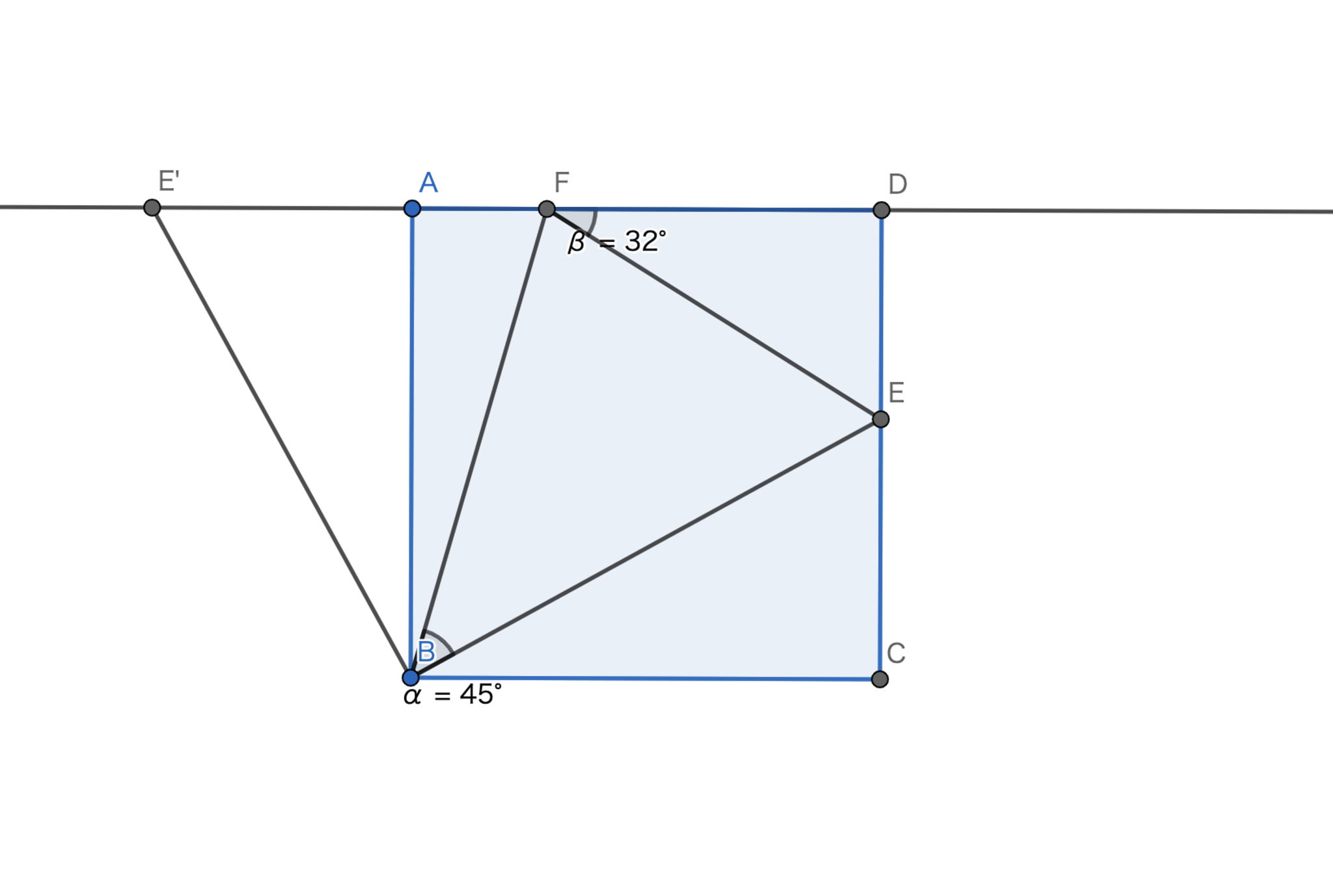
図1.問題1 -解説
等しい長さを作る
等しい長さをつくることで、合同な図形ができるなどして議論が進むことがあります。
三角形 \({ABC}\) の内部の点 \(P\) は以下を満たす。 \[\angle{PAB}=30°,\angle{PBA}=20°,\angle{PBC}=60°,\angle{PCB}=20°\] このとき、\(\angle{PCA}\) を求めよ。
難角問題は初めからうまくいくことは読めないです。 対称性を駆使して隠れた条件を発見していくことが大事になります。
解答
簡単な角度計算によって、\(\angle{APB}=\angle{APC}=130°\) となるので \(PB=PD\) なる点 \(D\) をとれば、\(\angle{PDB}=40°\) と併せて \(\triangle{ABD}\) が正三角形であるとわかる。 さらに、簡単な角度計算を行うことで \(BD=CD\) となるので \(AD=CD\) となり、\(\angle{DCA}=\boxed{10°}\) となる。
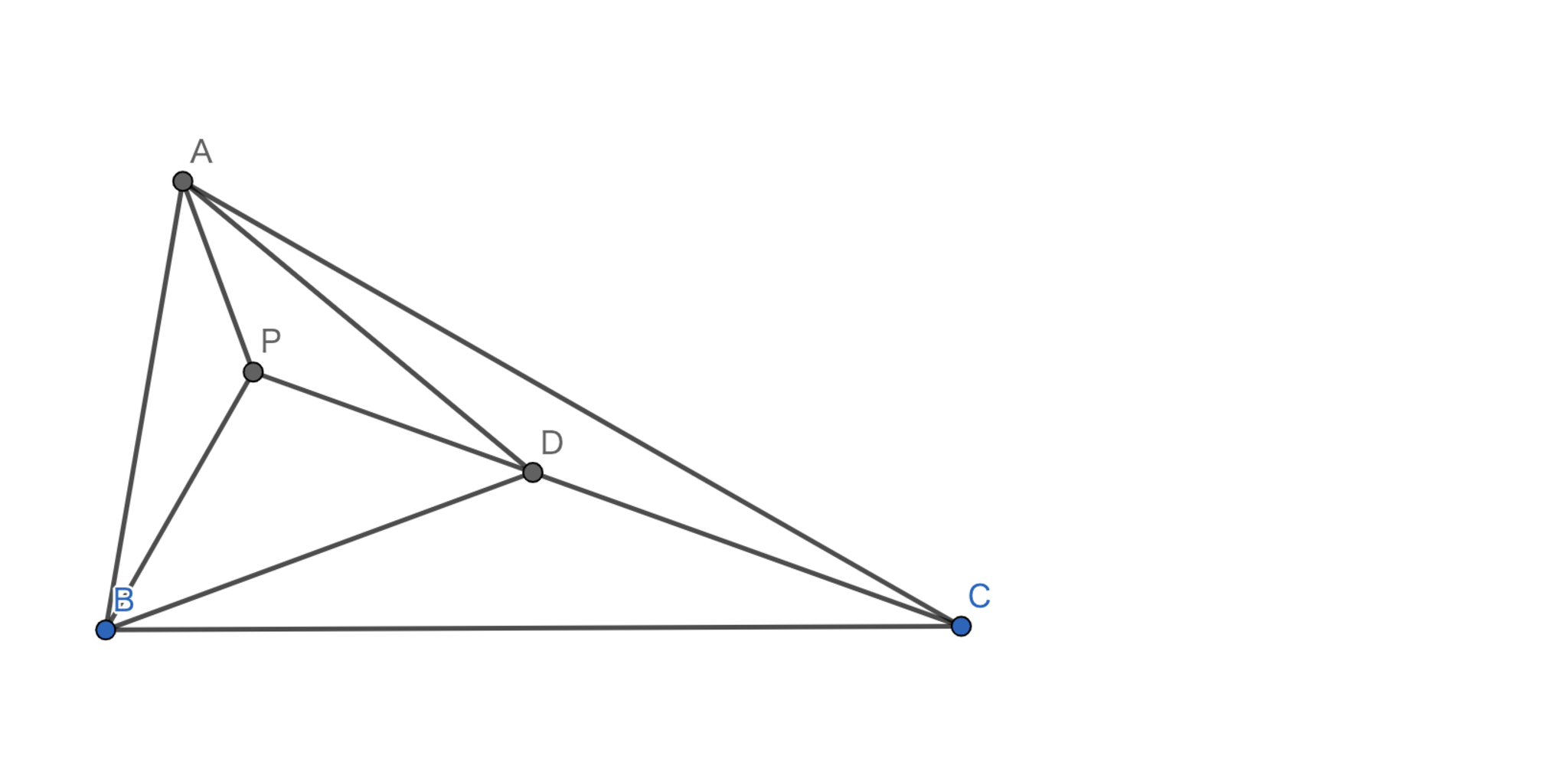
図2.問題2 -解説
対称移動
これは本当に重要な定石です。
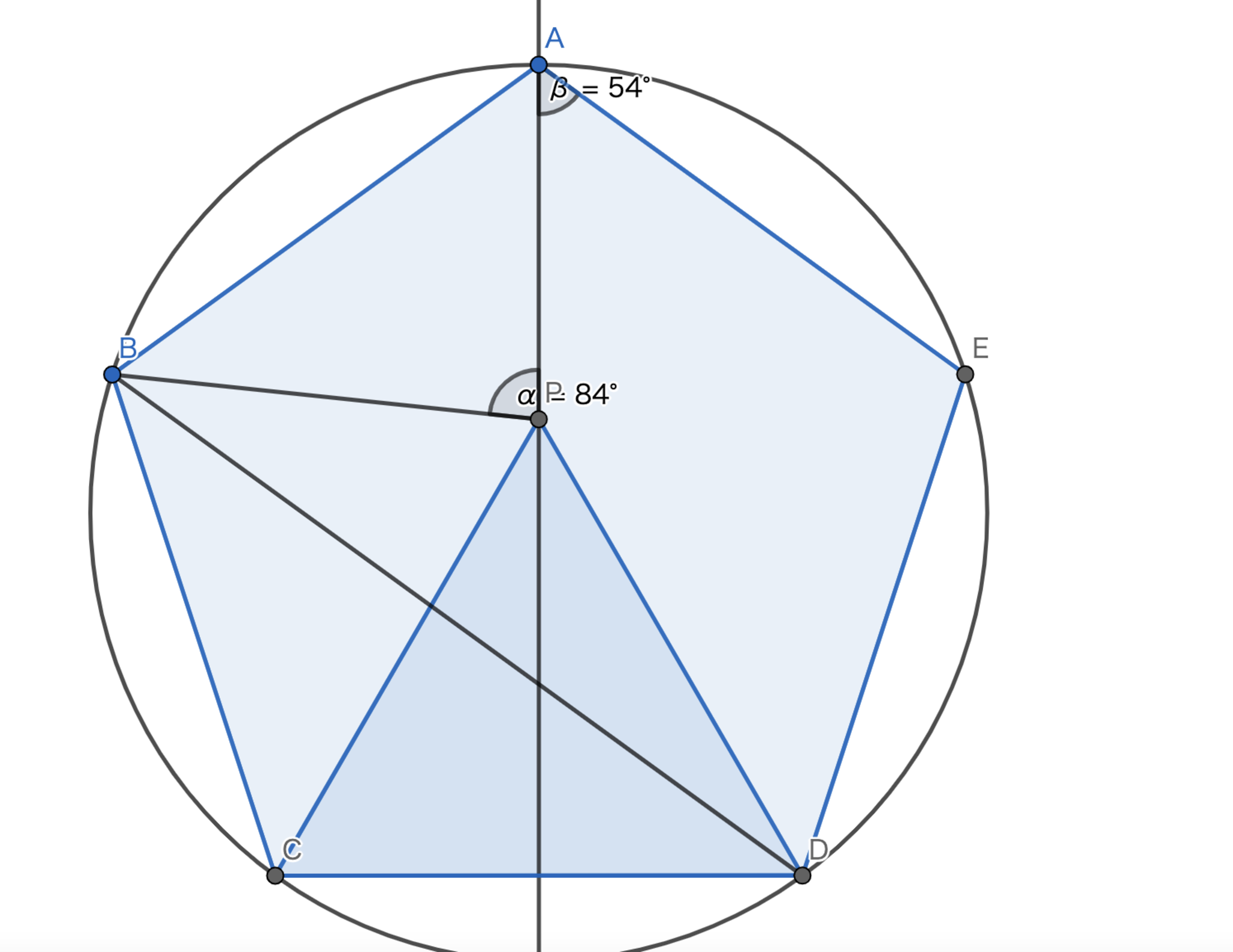
全ての内角が \(180°\) 未満である五角形 \(ABCDE\) において以下が成立しました。 \[AB=AE, \ BC=CD=DE, \ \angle{BAE}=22°,\ \angle{CAD}=11°, \ \angle{BCD}=91°\] このとき、\(\angle{CDE}\) の大きさを度数法で求めてください。
\(\angle{BAE}=22°\) で \(\angle{CAD}=11°\) はとっても怪しいです。 これはすなわち \(\angle{BAE}=2\angle{CAD}\) であることを表しています。
解答
\(\angle{BAE}=2\angle{CAD}\) なので \(B,E\) を \(AC,AD\) に関して対称移動させると一致する。この点を \(P\) とする。 このとき、\(\triangle{PCD}\) は条件より正三角形となる。 \(\angle{BCP}=31°,\angle{CPD}=60°\) である。 四角形 \(PEAB\) に着目すると \(\angle{BPE}=169°\) となる。 よって、\(\angle{DPE}=56.5°\) となり、\(\angle{CDE}=\boxed{127°}\) となる。
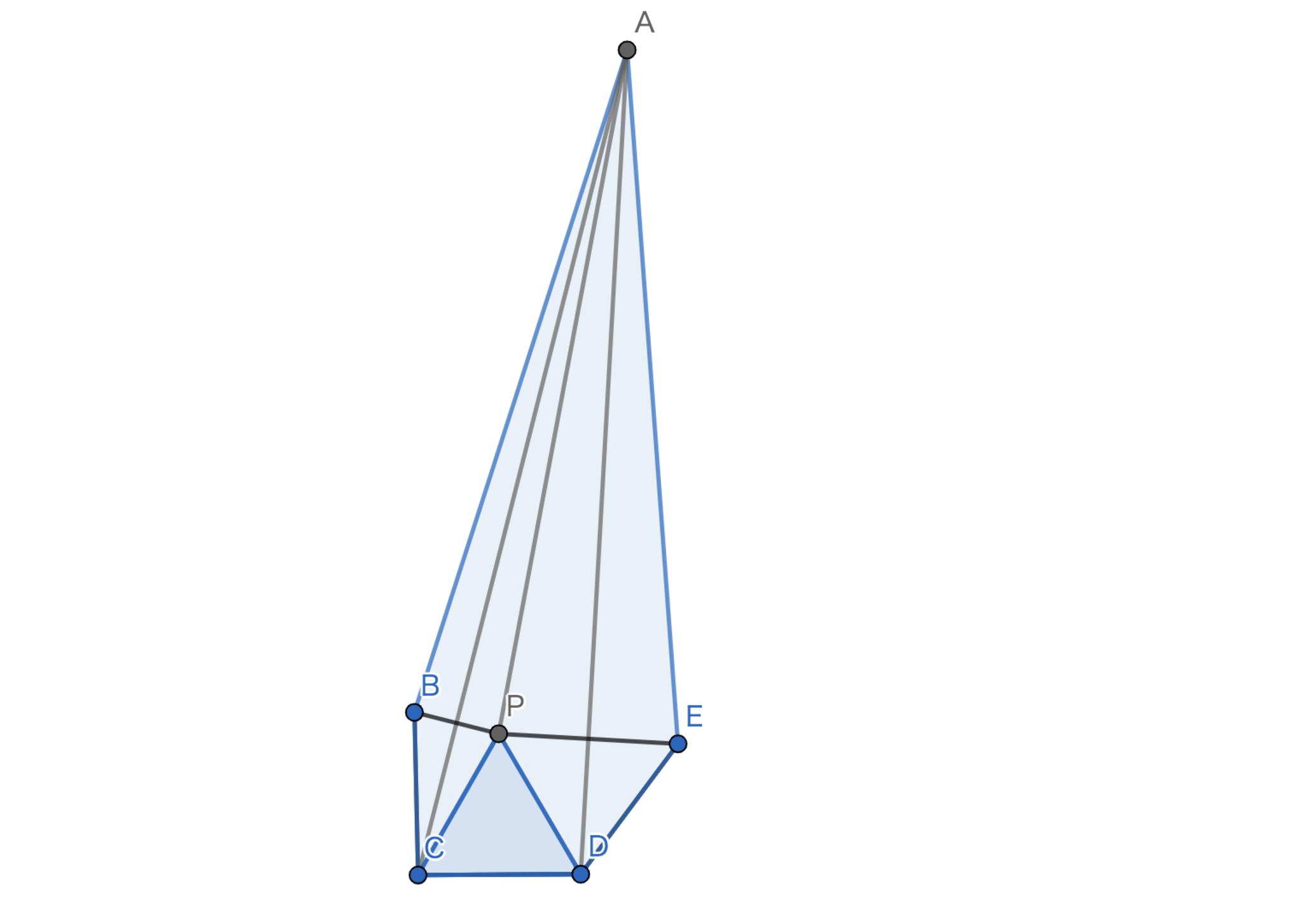
図3.問題3 -解説
作図可能性を考える
「図が一意に定まるには?」や「作図するには?」を考えると、うまくいくこともあります。
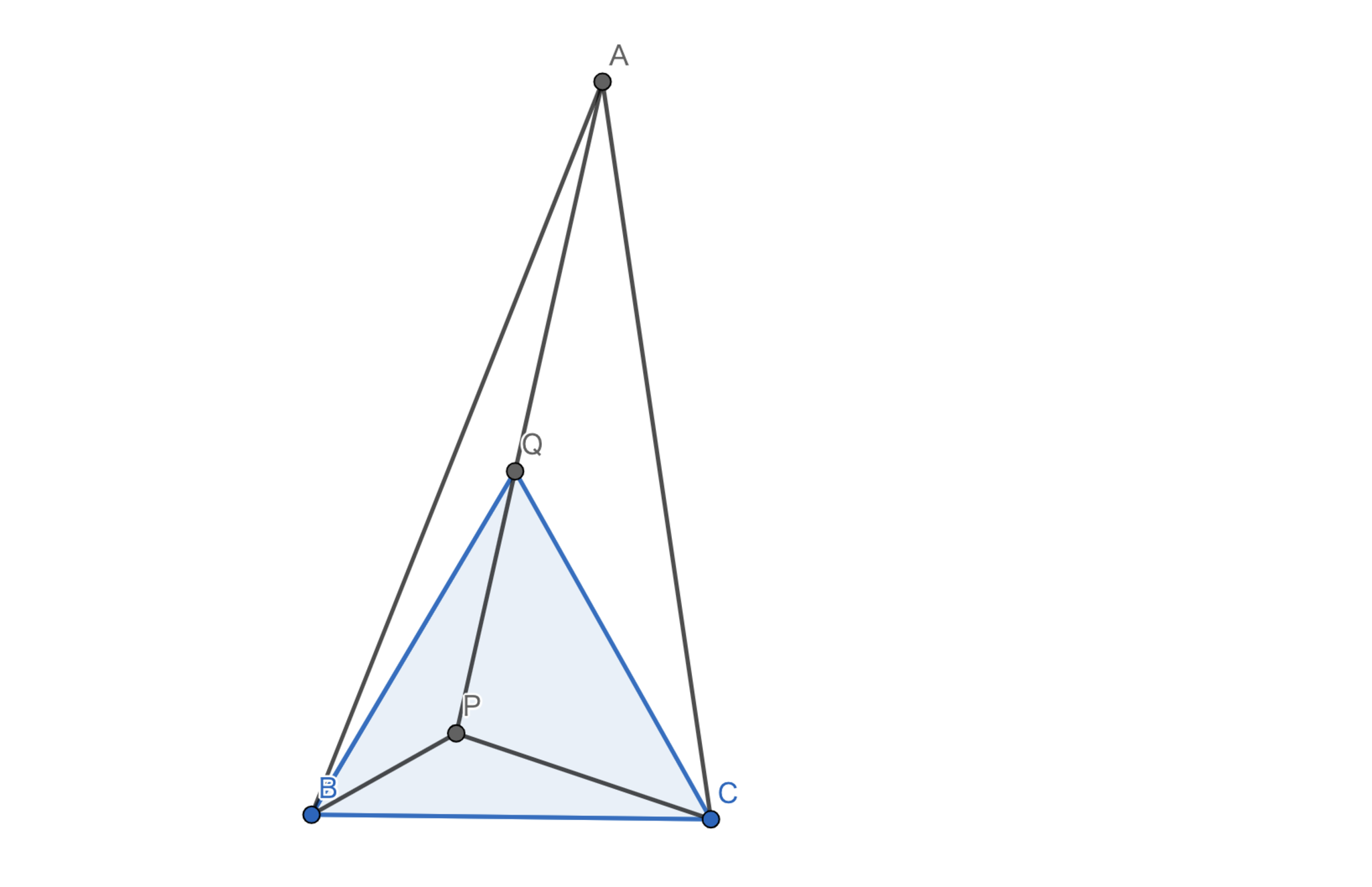
\(AB=AC\) なる二等辺三角形の内部に点 \(P\) をとったところ以下が成立した。 このとき、\(\angle{PAC}\) を求めよ。 \[\angle{BAC}=70°, \angle{PBC}=30°,\angle{APC}=150°\]
難角問題は普通のangle-chaseでは情報が足りないことが多いです。 大抵は特殊な"解ける"状況になっているのです。 ということで、その隠された特殊性を探し当てることが重要になってきます。 そこで役立つことがあるのが作図可能性です。
\(\angle{BAC}=70°\) を丁寧に作図するのは難しいですが、\(\angle{APC}=150°\) なら作図可能であるので、そちらを起点に考えていきます。
解答
三角形 \(OAC\) が正三角形になるような点のうち、\(P\) でない側にあるものを点 \(O\) とすれば、 \(P\) は \(O\) を中心とする半径 \(OA(=OC)\) の円上に存在する。 さらに、\(AB=AC=AO\) なので \(\angle{ABO}=\angle{AOB}=\frac{180°-(70+60)}{2}=25°\) を得る。 一方で、\(\angle{ABP}=25°\) なので \(B,P,O\) は共線である。 よって、円周角の定理より、\(\angle{PAC}=\frac{\angle{POC}}{2}=\boxed{\frac{35°}{2}}\) となる。
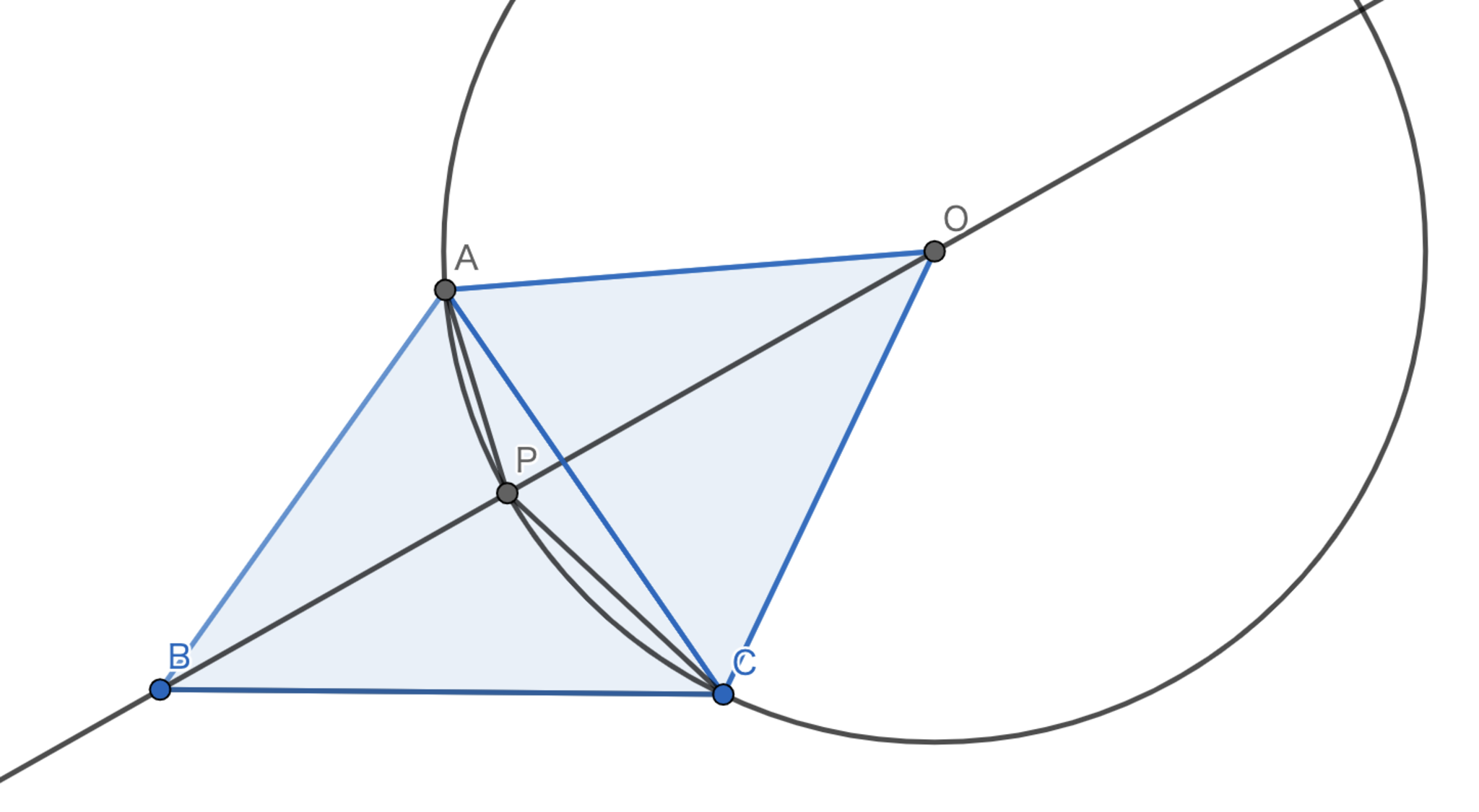
図4.問題4 -解説
正多角形を見抜く
正多角形を作りに行くことも有効です。
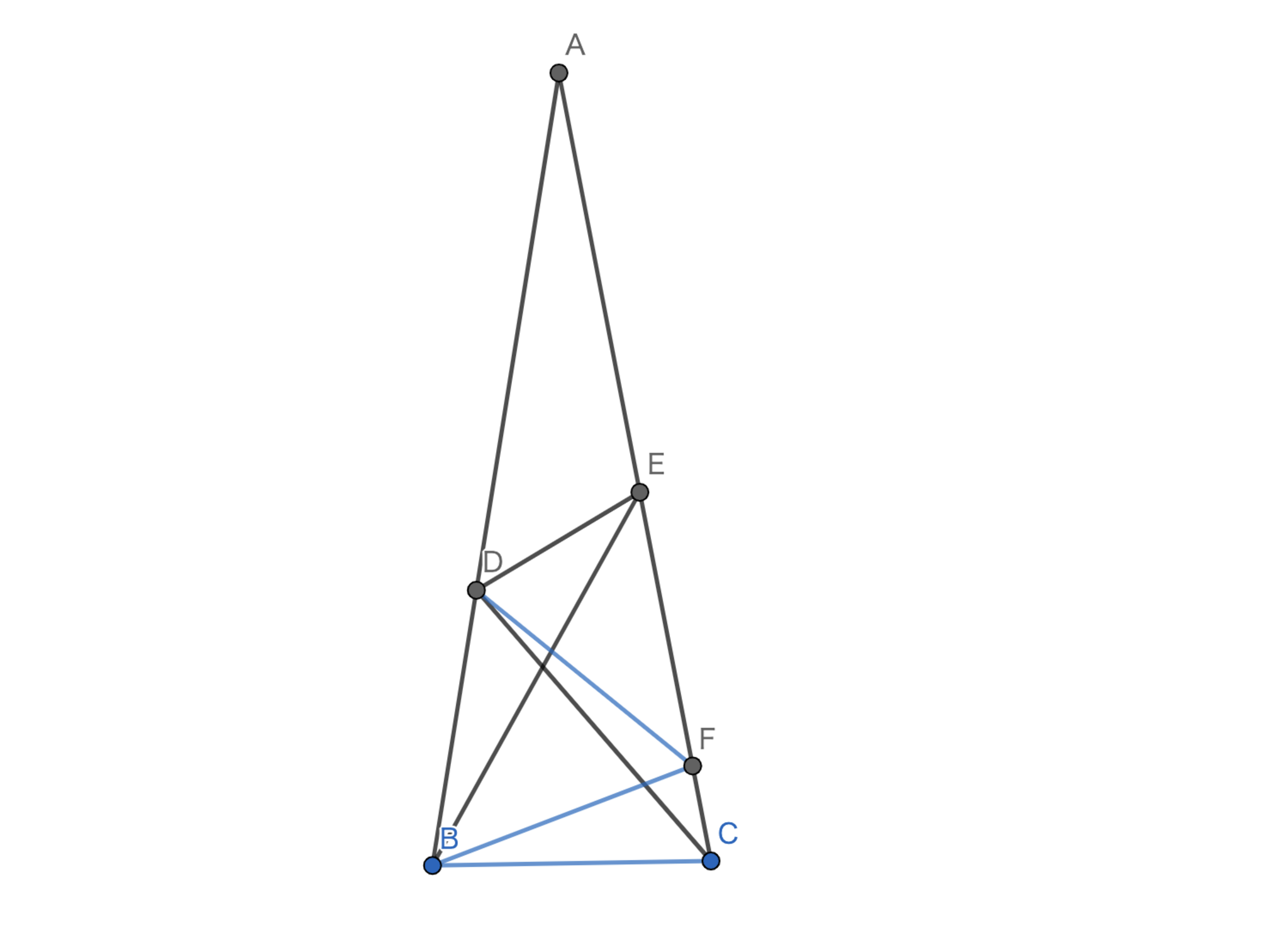
正五角形 \(ABCDE\) の内部の点 \(P\) は以下を満たす。 \(\angle{PAC}\) の大きさを求めよ。 \[\angle{ABP}=6°, \angle{AEP}=12°\]
\(6°\) を一つの角に持つような二等辺三角形の一つに \(6°,6°,168°\) という三角形があります。 \(168°\) を作図できれば \(6°\) を作図できることになります。 ここで気づきたいのが \(168=108+60\) です。これが何を意味するかわかりますか...?
解答
図のように、正三角形を成すように点 \(F\) を取ると \(B,P,F\) は共線となる。 \(\angle{PEA}=12°\) より、\(\angle{FPE}-\angle{PFE}=54°\) であるから \(AE=PE=FE\) である。 以上より、\(\angle{PAC}=\angle{PAE}-\angle{CAE}=84°-72°=\boxed{12°}\) である。
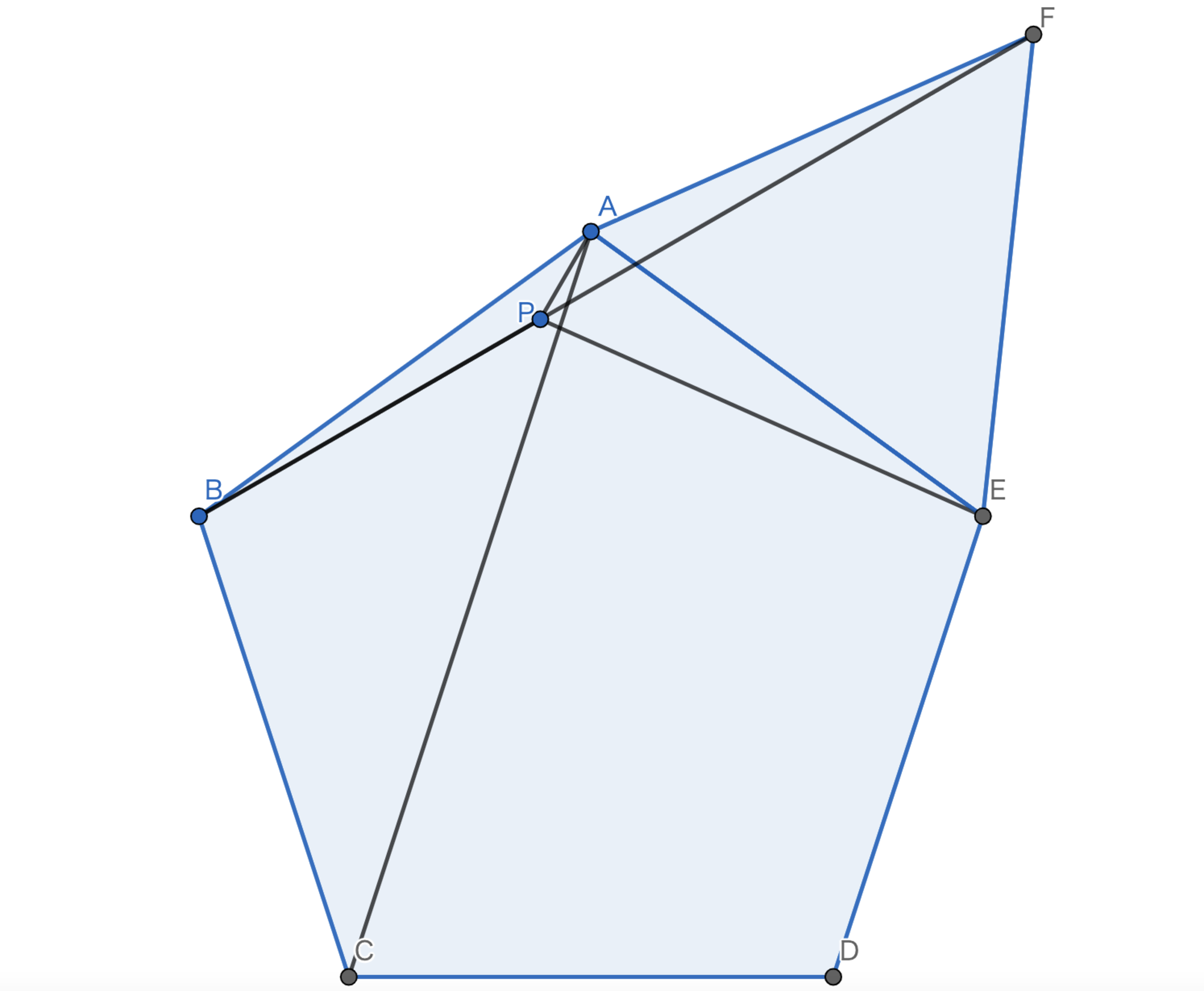
図5.問題5 -解説
連立法
simasimaさんによる難角求値問題の新手法です。あまりにも画期的だったので紹介しておきます。
simasimaさんの記事はこちら。
演習問題
ここからが本番です。いい感じの難易度の問題を用意しました。 中学受験レベルから、JMO後半レベルまでを用意しています。
正方形 \(ABCD\) の辺 \(CD,DA\) 上に点 \(E,F\) が存在して \(\angle{EBF=45°},\angle{DFE}=x°\) を満たすとき \(\angle{BEC}\) の大きさを \(x\) を用いて表せ。
平行四辺形 \(ABCD\) は \(\angle{DBC}=15°,\angle{ACB}=30°\) を満たす。 このとき、\(\angle{BAC}\) の大きさを求めよ。
正五角形 \(ABCDE\) の内部の点 \(P\) が以下を満たした。 このとき、 \(\angle{BDP}\) の大きさを求めよ。 \[\angle{BPA}=84°,\angle{PAE}=54°\]
\(AB=AC,\angle{BAC}=20°\) なる二等辺三角形 \(ABC\) の辺 \(AB,AC\) 上に点 \(D,E\) をとったところ以下が成り立った。 \(\angle{BED}\) の大きさを求めよ。 \[\angle{CBE}=60°, \ \angle{DCB}=50°\]
三角形 \(ABC\) の内部の点 \(P\) が以下を満たす。 \(\angle{PBC}\) の大きさを求めよ。 \[\angle{BAP}=\angle{CAP}=14°, \ \angle{PBA}=2\angle{PCA}=32°\]
ハイパー良問ですね。
三角形 \(ABC\) の内部の点 \(P\) が以下を満たす。 \(\angle{PBC}\) の大きさを求めよ。 \[\angle{BAP}=9°, \ \angle{CAP}=21°, \ \angle{PBA}=39°, \ \angle{PCA}=63°\]
すこし手荒な方法もお見せしておこうと思います。
証明を表示/非表示三角形 \(ABC\) および内部の点 \(P\) が以下の条件を満たします。 \(\angle{PAC}\) の大きさを求めてください。 \[\angle{BPA}=\angle{BPC}=\angle{ABP}+120°=141.4°, \ \angle{PBC}=30°\]
凸四角形 \(ABCD\) が \[\tan{\angle{BAC}} = \sqrt{3}, \ \tan{\angle{CAD}} = 3\sqrt{3}\] \[\tan{\angle{ABD}} = \frac{\sqrt{3}}{5}, \ \tan{\angle{CBD}} = \frac{9\sqrt{3}}{11}\] をみたすとき、\(\tan{\angle{ACD}}\) の二乗は互いに素な正の整数 \(a,b\) を用いて、\(\frac{a}{b}\) と表されるので、\(a+b\) の値を求めてください。
角度の代わりに、\(\tan\) の情報が与えられるタイプの問題ですね。おもしろいです。
凸四角形 \(ABCD\) は \(AD=CD, \ BD=BC, \ \angle{ADC}=168°, \ \angle{ABC}=66°\) を満たす。 このとき、 \(\angle{BAD}\) の大きさを求めよ。