Euler線の多角形への拡張
Euler線はとてもシンプルで美しい初等幾何の定理ですが、一般的には三角形の範囲でしか議論されません。 そこで、今回は無理やり多角形に拡張するとどのようになるのかを考えてきたので紹介します。それでは、よろしくお願いします。
前提
正三角形でない任意の三角形において外心 \(O\) , 重心 \(G\) , 垂心\(H\) はこの順で一直線上に並び、\(|OG|:|GH|=1:2\) が成立する。
のちの証明に合わせて、複素座標で証明します。
証明
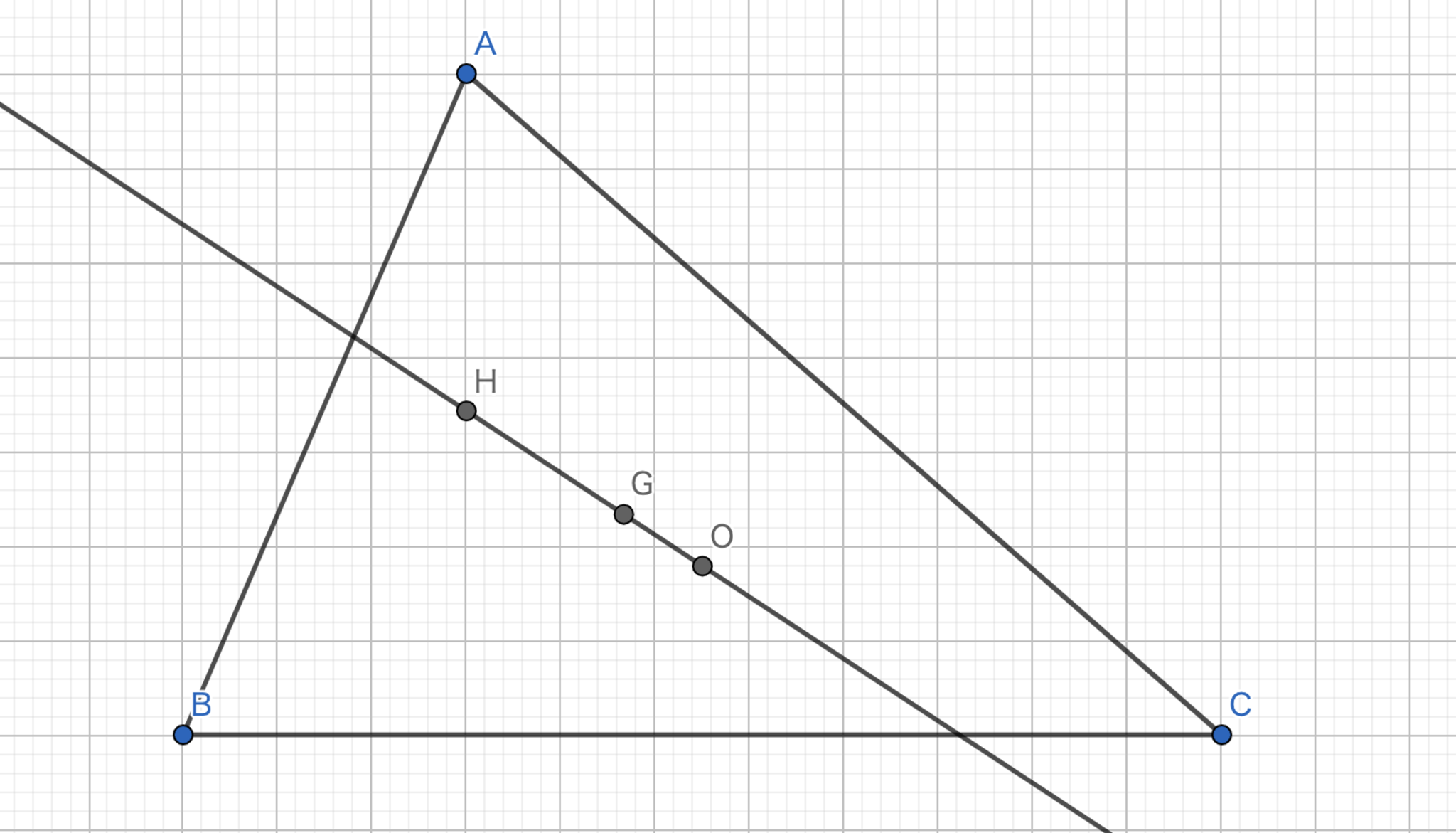
図1.Euler線
複素平面で考える。三角形 \(ABC\) の外接円の半径を \(1\) としても一般性を失わない。 外接円の中心 \(O\) の座標を \((0)\) , \(A,B,C\) の座標をそれぞれ \((a),(b),(c)\) とする。
・このとき、重心 \(G\) の座標は \(\frac{a+b+c}{3}\) となる。
・ \(A\) から \(BC\) へと下ろした垂線の式は \(z-bc\overline{z}=a-\frac{bc}{a}\) となる。
・ \(C\) から \(AB\) へと下ろした垂線の式は \(z-ab\overline{z}=c-\frac{ab}{c}\) となる。
・これらを連立して垂心 \(H\) の座標は \(a+b+c\) となる。
このとき、\(O,G,H\) は一直線上にあり、\(|OG|:|GH|=1:2\) が成立する。したがって、題意は示された.。\(\blacksquare\)
このことから、単位円周上の三点 \(a,b,c\) を頂点とする三角形の垂心は \(a+b+c\) と表されることが分かります。
主張
円に内接する \(n\) 角形 \(A_{1}A_{2}\cdots A_{n}\) の重心を \(G\) 、外心を \(O\)、三角形 \(A_{1}A_{2}A_{3},A_{2}A_{3}A_{4},\cdots,A_{n}A_{1}A_{2}\) の垂心をそれぞれ \(H_{1},H_{2},\cdots,H_{n}\) とする。
\(n\) 角形 \(H_{1},H_{2},\cdots,H_{n}\) の重心を \(G'\) とすると以下が成り立つ。
\(O,G,G'\) は一直線上に並び、\(|OG|:|GG'|=1:2\) となる。
こちらの証明はかなり平易ですので、是非チャレンジしてみてください。
証明
複素平面で考える。 \(n\) 角形 \(A_{1}A_{2}\cdots A_{n}\) の外接円の半径を \(1\) としても一般性を失わない。 外接円の中心 \(O\) の座標を \((0)\) , \(A_{i}\) の座標をそれぞれ \((a_{i})\) とする。(以下、添字は \(n\) を法とする。)
・このとき、重心 \(G\) の座標は \(\frac{1}{n}\left(A_{1}+A_{2}+\cdots+A_{n}\right)\) となる。
・また、単位円周上の三点 \(a,b,c\) を頂点とする三角形の垂心は \(a+b+c\) と表されるから、\(H_{i}=A_{i}+A_{i+1}+A_{i+2}\) となる。それらの重心 \(G'\) は以下のように計算できる。 \[ \frac{1}{n}\sum_{i=1}^{n}H_{i}=\frac{1}{n}\sum_{i=1}^{n}(A_{i}+A_{i+1}+A_{i+2})=\frac{3}{n}\left(A_{1}+A_{2}+\cdots+A_{n}\right) \]
したがって、\(O,G,G'\) は一直線上に存在し、\(|OG|:|GG'|=1:2\) が成立する。これより、題意は示された。\(\blacksquare\)