接線の交点を結んでできる共点
今回は、そこそこ難しい幾何の問題を解説していきます。それでは、よろしくお願いします。
問題
円 \(\Omega\) に内接する六角形 \(ABCDEF\) は \(|AB|=|BC|,|CD|=|DE|,|EF|=|FA|\) を満たす。 \(\Omega\) の \(A,B,C,D,E,F\) における接線をそれぞれ \(L_{A},L_{B},L_{C},L_{D},L_{E},L_{F}\) とする。 \(L_{A}\) と \(L_{C}\) の交点を \(B'\), \(L_{B}\) と \(L_{D}\) の交点を \(C'\), \(L_{C}\) と \(L_{E}\) の交点を \(D'\), \(L_{D}\) と \(L_{F}\) の交点を \(E'\), \(L_{E}\) と \(L_{A}\) の交点を \(F'\), \(L_{F}\) と \(L_{B}\) の交点を \(A'\) とするとき、\(A'D',B'E',C'F'\) は一点で交わることを示せ。
複素座標、射影幾何を使わないとかなり難しくなると思います。
解説
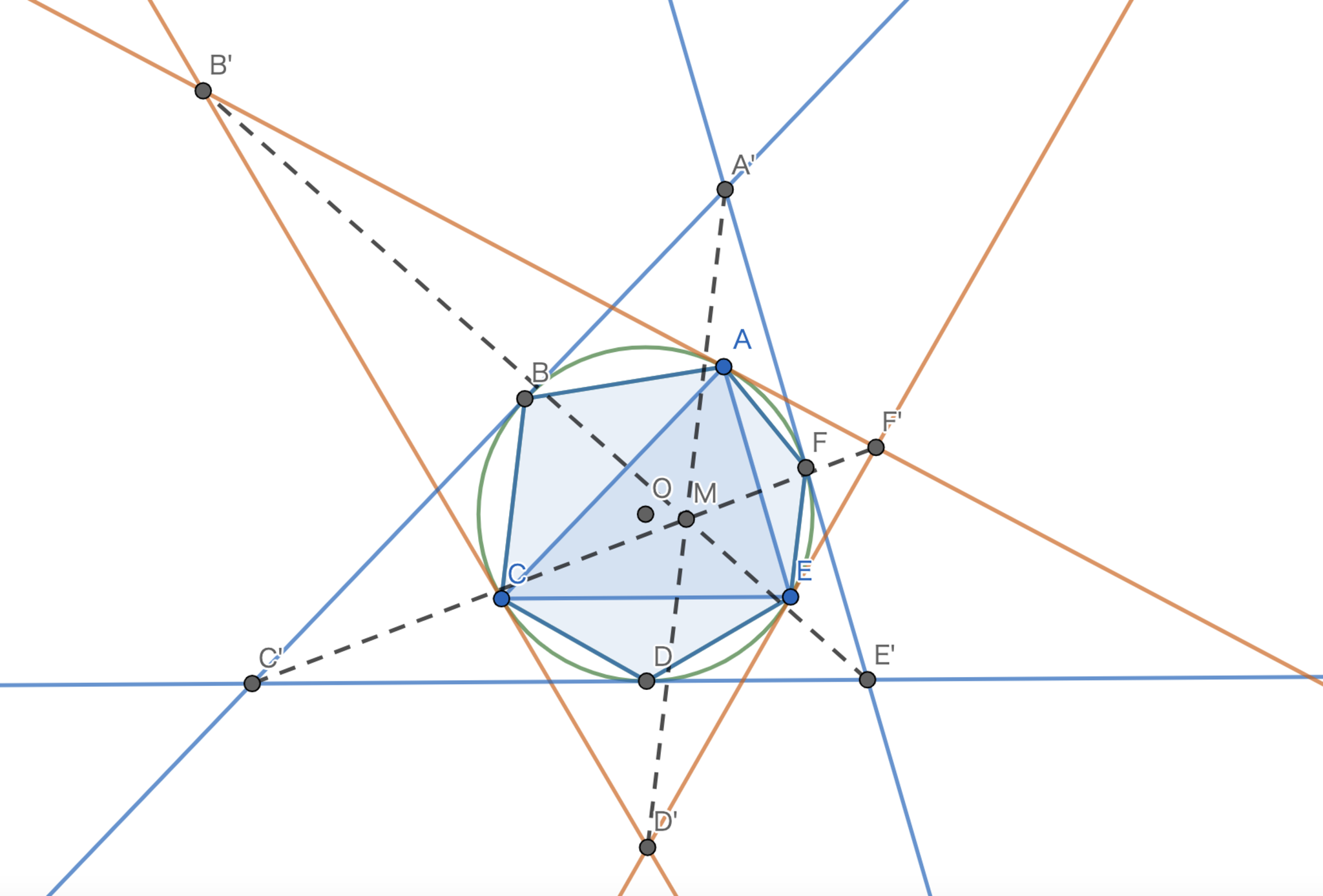
図1.問題文の図形
解法1(複素座標による解法)
\[ A(a^2) \ B(-ac) \ C(c^2) \ D(-ce) \ E(e^2) \ F(-ea) \ \] となるようにうまく座標を定める。このとき \[ A'(-\frac{2ace}{c+e}) \ B'(\frac{2a^{2}c^{2}}{a^{2}+c^{2}}) \ C'(-\frac{2ace}{e+a}) \ D'(\frac{2c^{2}e^{2}}{c^{2}+e^{2}}) \ E'(-\frac{2ace}{a+c}) \ F'(\frac{2e^{2}a^{2}}{e^{2}+a^{2}}) \ \] が得られる。\(A'D'\) の式を考える。\(\bar{A'}(-\frac{2}{a\left(c+e\right)}),\bar{D'}(\frac{2}{c^{2}+e^{2}})\) であることに留意して、 \[ A'D':(\bar{A'}-\bar{D'})z-(A'-D')\bar{z}=\bar{A'}D'-A\bar{D'} \\ \Longleftrightarrow -\frac{2c^{2}+2e^{2}+2ac+2ae}{a\left(c+e\right)\left(c^{2}+e^{2}\right)}z+\frac{2ce\left(ac^{2}+ae^{2}+c^{2}e+ce^{2}\right)}{\left(c+e\right)\left(c^{2}+e^{2}\right)}\overline{z}=-\frac{4c^{2}e^{2}}{a\left(c+e\right)\left(c^{2}+e^{2}\right)}+\frac{4ace}{\left(c+e\right)\left(c^{2}+e^{2}\right)} \\ \Longleftrightarrow -\left(ac+ae+c^{2}+e^{2}\right)z+ace\left(ac^{2}+ae^{2}+c^{2}e+ce^{2}\right)\overline{z}=2a^{2}ce-2c^{2}e^{2} \] となる。ここで、\(z=-(ac+ce+ea)\) を代入する。(内心の座標) \[ \left(ac+ae+c^{2}+e^{2}\right)\left(ac+ce+ea\right)-ace\left(ac^{2}+ae^{2}+c^{2}e+ce^{2}\right)\left(\frac{1}{ac}+\frac{1}{ce}+\frac{1}{ca}\right)=2a^{2}ce-2c^{2}e^{2} \] が成り立つので \(A'D'\) は内心を通る。このとき、対称性より \(B'E',C'F'\) も内心を通るので三直線は一点、特に内心で交わることが示された。
(方針としては、うまく三点\(A,C,E\)の座標を定めて使う文字数を減らして計算を楽にするというものです。 初等的に考えてみると、角の二等分線が登場することに気付けると思いますそこで、うまく座標設定ができることを思いつくでしょう。 また、計算は内心などの偏角の議論が必要になりやや難しいです。こちらが参考になると思います。)