交流の複素数表示(高校生向け)

今回は、物理の交流を複素数で解く方法を丁寧に解説していきたいと思います。それでは、よろしくお願いします。

交流とその周辺の基本

直流回路三種の神器

まずは、交流の前に直流でも使える基本的な三つの式について確認してみます。

回路を扱う上では最も基本的な式です。(基本的ですが、導出は簡単ではありません。誘導が欲しいレベルです。)今回は導出は省きます。

ちなみに、符号はあまり気にする必要はありません。実際に使うときは、起電力の大きさをこの式で出して、向きは別で考えることが多いです。 こちらも導出は省きますが、Lの中身くらいはすぐに計算できるようにしておいた方が良いですね。

今回は、もう少し別の形で使います。\(I = \frac{d Q}{d t}\) を利用して、\(I = C\frac{d V}{d t}\) にします。 さらに、上二つと表示を揃える(「\(V=\)」にする)ために、両辺を積分して、\(V = \frac{1}{C}\int{I} dt\) としておきます。

交流回路の瞬時値

先ほど紹介した三つの法則は、交流回路のてきとうな瞬間を切り取っても成立します。これを用いて以下の回路を考えていきましょう。

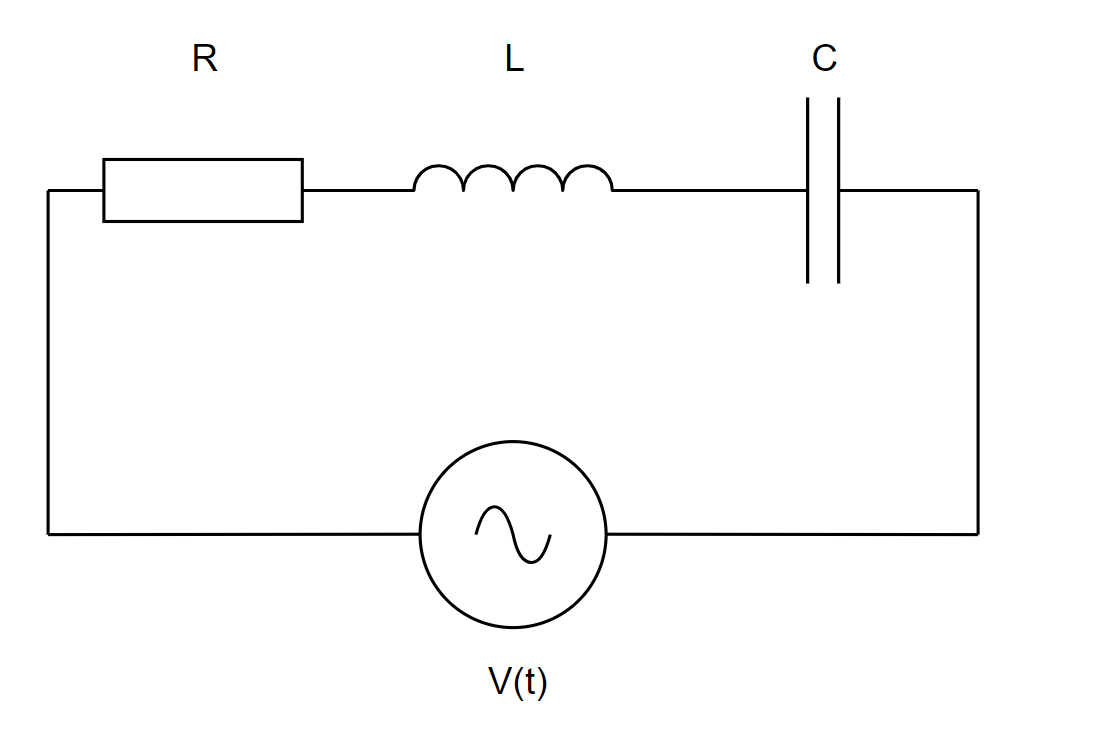
図1.RLC直列回路

交流電源と、抵抗値 \(R\) の抵抗、自己インダクタンス \(L\) のコイル、静電容量 \(C\) のコンデンサ が直列につながっている回路です。 この回路について電流を \(I_0 \sin{\omega t}\) として、キルヒホッフの法則を考えます。 \[V(t) = R I_0 \sin{\omega t} + L\frac{d}{dt}(I_0\sin{\omega t}) + \frac{1}{C} \int{I_0\sin{\omega t}} dt\] 積分や微分を実行して、 \[V(t) = R I_0 \sin{\omega t} + L\omega I_0\cos{\omega t} - \frac{1}{C\omega} I_0\cos{\omega t} dt\] を得ます。ここで、積分定数は細かい理由(減衰するなど)から無視できます。瞬時値で交流を扱うと、ここからさらに三角関数の合成などを行っていく必要があり、かなり骨が折れるものになったりします。 さら、交流電流を時刻 \(t\) の関数で表すメリットは薄いです。結局、時刻の基準をどこに置くかで \(t\) の値なんて変わってしまいますし、それよりは振幅や位相などのほうが大事だということはわかると思います。 実際に、実用的な文脈で瞬時値を考えることはほとんどないです。 ということで、これらを踏まえて、もう少し交流回路をうまく表現する方法はないでしょうか？今回は、こちらを考えていきます。

交流の情報は"位相差"と"実効値"だけ

交流電流・交流電圧が持つ最大の情報は位相差と実効値です。

実効値

実効値が大事だということはかなりわかりやすいと思います。電流や電圧の大きさがどれくらいなのかは抑えておきたい情報です。直列でいうところの、\(R,V,I\) などに対応するもので、当然必須です。 ここで、「実効値じゃなくて振幅ではだめなの？」と思うかもしれませんが、ぶっちゃけどちらも持っている情報としては等価(\(V_0 = \sqrt{2} V\) のように、一方がわかればもう一方もわかる)ですので、アイデアとしては同じです。 ただし、振幅ではなく、実効値にしておくと、後々出てくる電力の計算などで少し楽をすることができるのでそのようになっています。 要は、"大きさ"が重要ということです。

位相差

先ほども言った通り、時刻 \(t\) は基準の時刻や、複雑さなどから不便であり、そもそも電気回路を考えるうえで、ある一瞬に着目する機会もないです。 結局は電力を考えたり、素子の働きを考えるうえで、一瞬に着目する意味はあまりないです。その代わりに導入するのが、位相差です。

先ほど導いた回路方程式をもう一度載せてみます。 \[V(t) = R I_0 \sin{\omega t} + L\omega I_0\cos{\omega t} - \frac{1}{C\omega} I_0\cos{\omega t} dt\] この式において、 \[\cos{x} = \sin{\left(x + \frac{\pi}{2}\right)}, \ -\cos{x} = \sin{\left(x - \frac{\pi}{2}\right)}\] を踏まえて変形すると、 \[V(t) = R I_0 \sin{\omega t} + L\omega I_0\sin{\left(\omega t + \frac{\pi}{2}\right)} + \frac{1}{C\omega} I_0\sin{\left(\omega t - \frac{\pi}{2}\right)} dt\] となり、この式から、時刻 \(t\) がいくらであってもコイル、コンデンサの電圧はそれぞれ電流に対して \(\frac{\pi}{2}, \ -\frac{\pi}{2}\) 進んでいます。 これが位相差です。時刻 \(t\) を無視してこの回路方程式を考えられるようになります。この位相差は合成インピーダンスなどを考える際にとても重要になります。

その他の情報

他にも、角振動数(周波数)も交流を特徴づける重要な情報です。 ですが、この角振動数はどんな素子でも共通しており、各素子で(\(\sin\) の中身に)差が出ないのでその点において気にする必要はありません。 例えば、さっきの \[V(t) = R I_0 \sin{\omega t} + L\omega I_0\sin{\left(\omega t + \frac{\pi}{2}\right)} + \frac{1}{C\omega} I_0\sin{\left(\omega t - \frac{\pi}{2}\right)} dt\] において、\(\sin\) の中身の \(\omega t\) の部分が共通していますね。 \(\sin\) の中身以外にも係数として \(\omega\) がありますが、これはあくまでも交流の情報の外側についている係数というイメージです。

交流の情報を複素数に詰めこむ

大きさをノルムに、位相差を偏角に

それでは本題の複素数です。実効値と位相差を複素数に詰めていきたいと思います。 まず最初に情報を詰めてみて、そのあとに何がうれしいのか？なぜうまくいくのか？を説明します。とりあえず受け入れてください。

電圧の実効値を \(V\) 、初位相(基準との位相差)を \(\varphi\) とします。 つまり、 \[V(t) = \sqrt{2}V\sin{(\omega t + \varphi)}\] とします。 このとき、そのような交流電圧を表す複素数 \(\dot{V}\) を以下を満たすように定めます。 (このように \( \dot{V} \) と、ドットをつけて表記するのは、複素数によるベクトル、複素ベクトルだからです。) \[arg(\dot{V}) = \varphi, \ |\dot{V}| = V\] 例えば、実効値が \(1\) で、位相差が \(\varphi\) の交流電圧を表現するときには以下のような複素数になります。 \[\dot{V} = \cos{\varphi} + j\sin{\varphi}\] ここで、\(j\) は虚数単位です。\(i\) でないのは、電流との混同を防ぐためです。 複素数平面にプロットするとこんな感じになります。

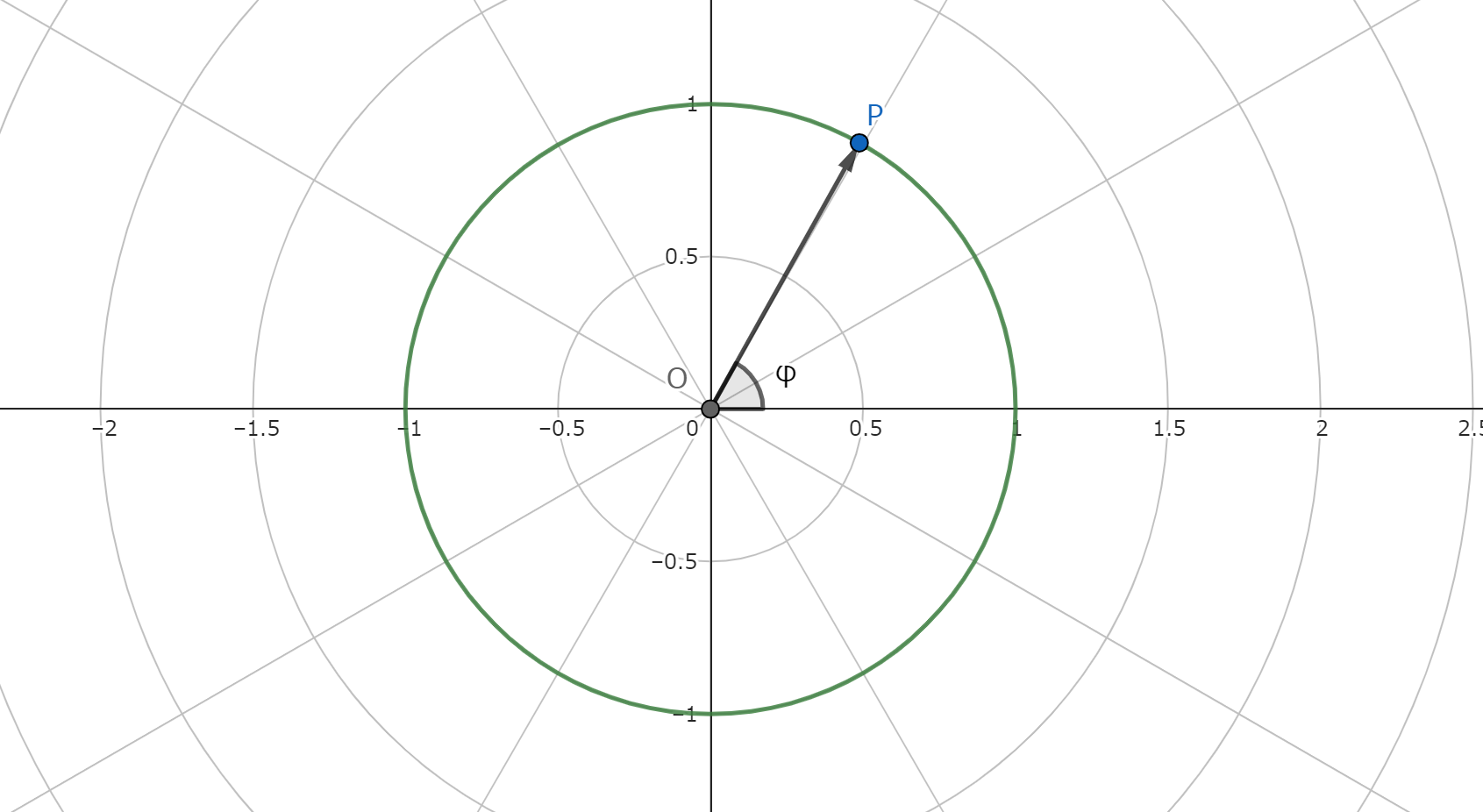
図2.複素平面にプロットする。

既に数学Ⅲを学習した人ならば、これがいわゆる極座標に対応していることがわかると思います。 極座標の考え方にもとづけば、角度と大きさを決めてあげれば点の座標は一意に定まることがわかると思います。 確かに、情報を詰め込むことはできました。交流電流などについても同様に表現します。

複素数表示の利点

何がうれしい？

→コイルとコンデンサでもオームの法則(?)が成立し、さらに合成インピーダンスなども直流と同じように計算できることが嬉しいです！

順を追って確認していきます。インピーダンスにも、位相と大きさの情報が含まれていますのでドットが付いています。

コイル

自己インダクタンス \(L\) のコイルに電流 \(\dot{I} (= I(\cos{0}+j\sin{0}) = I)\) が流れるときに、 自己誘導起電力の大きさは \(\omega L\) 倍され、位相は電流に対して \(\frac{\pi}{2}\) だけ進みました。これを複素数で表現してみます。 大きさはそのままかければよくて、位相は \(\cos{\frac{\pi}{2}} + j\sin{\frac{\pi}{2}} = j\) をかけることで表現できます。 \[\dot{V} =j\omega L \dot{I} (= j\omega L I)\] となります。確かに純虚数なので、偏角＝位相差は90°となっています。この、\(j\omega L\) のことをコイルのインピーダンスと呼びます。

角振動数が \(\omega\) と与えられていたら、インピーダンスが \(j\omega L\) であるから、オームの法則(改)を使って、位相と電圧の実効値がわかります。 重要なのは、オームの法則っぽい見た目なのに位相の情報が含まれているということです。

コンデンサ

静電容量 \(C\) のコンデンサに電流 \(\dot{I} (= I(\cos{0}+j\sin{0}) = I)\) が流れるときに、 コンデンサにかかる電圧の大きさは \(\frac{1}{\omega C}\) 倍され、位相は電流に対して \(-\frac{\pi}{2}\) だけ進みました。これも同様に複素数で表現してみます。 \[\dot{V} =-j \frac{1}{\omega C} \dot{I} \left(= -j\frac{1}{\omega C}I \right)\] となります。こちらも同様に、コンデンサのインピーダンスを \(-j\frac{1}{\omega C}\) となります。

抵抗

抵抗は面白みがないですが一応。 コイルコンデンサと同様にして考えることで、抵抗のインピーダンスは \(R\) となります。

直列回路の合成インピーダンス

これすごくないですか？例として、最初に挙げたRLC直列回路の合成インピーダンスを求めてみます。

図1(再掲).RLC直列回路

抵抗、コイル、コンデンサのインピーダンスはそれぞれ \(R,j\omega L, -j\frac{1}{\omega C}\) なので、 合成インピーダンス \(\dot{Z}\) は \[\dot{Z} = R + j\left(\omega L - \frac{1}{\omega C}\right)\] となります。

並列回路の合成インピーダンス

慣れ親しんだ式ですね。同様に、シンプルなRLC並列回路の合成インピーダンスを求めてみます。

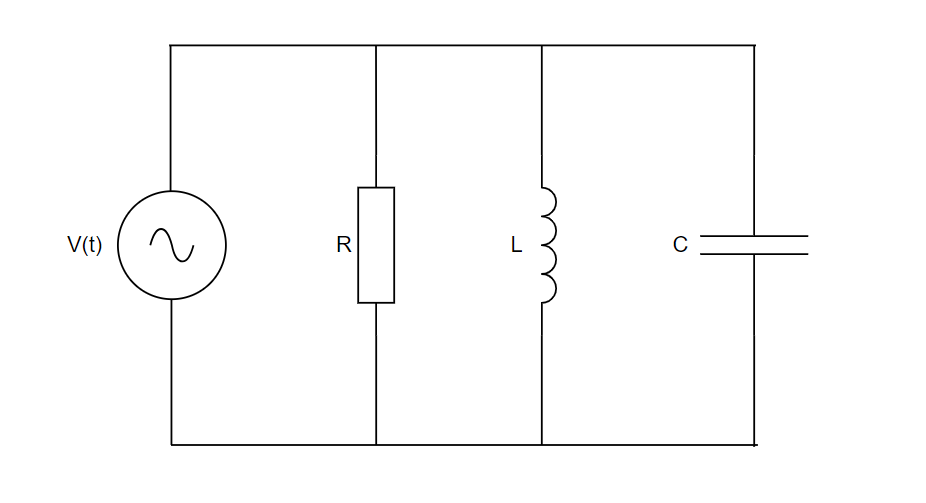
図3.RLC並列回路

抵抗、コイル、コンデンサのインピーダンスはそれぞれ \(R,j\omega L, -j\frac{1}{\omega C}\) なので、 合成インピーダンス \(\dot{Z}\) は \[\frac{1}{\dot{Z}} = \frac{1}{R} + \frac{1}{j\omega L} + \frac{1}{\left(-j \frac{1}{\omega C}\right)}\] を満たすので、 \[\dot{Z} = \frac{1}{\frac{1}{R} + j\left(\omega C -\frac{1}{\omega L}\right)}\] となります。分母分子に\(\frac{1}{R} - j\left(\omega C -\frac{1}{\omega L}\right)\) をかけて整理しても良いですが、あまり綺麗にならないのでやめておきます。

消費電力

"消費電力"という単語は平均の消費電力のことです。

\(\dot{I}\) や \(\dot{V}\) を実数とすれば、\(Re(\dot{V}\dot{I})\) ということです。 ここらへんの基本事項に関しては、複素数特有の要素はないです。 消費電力を考える際に、実効値(都合の良いような係数をつけた値)を使っていることに注意しましょう。

複素数表示の原理

正直言うと、これを書くのには苦労しました。かなりあいまいですし、あっているのかわかりません。僕のお気持ちです。お手柔らかに。

複素数表示を活用することで、四則演算で大きさと位相差の二つを同時に扱えるようになっただけでなく、合成抵抗などについても直流と同じように考えられるようになりました。 少しだけ、この原理のお気持ちを説明しておきます。別に、理解する必要はないです。

大きさ

これは複素数の以下の性質がかかわっています。 \[|Z_1 \times Z_2| = |Z_1| \times |Z_2|\] これで、大きさの情報は伝わります。

位相差

これも複素数の以下の性質が重要になってきます。 \[arg(Z_1 \times Z_2) = arg(Z_1) + arg(Z_2)\] これで、掛け算をすることによって、位相は足し引きされて都合よく伝わります。

合成インピーダンス

上二つに比べると、合成インピーダンスが直流と同じように計算できるという事実はかなり非自明なように思えるかもしれません。 しかし、逆に「なぜ(教科書的な)交流の計算では合成インピーダンスが直流と同じように計算できないのか？」を考えると、位相差が原因であることが分かるともいます。 位相差さえ考慮できれば、当然合成インピーダンスは計算できるのです。

もう少しフランクに言うと、実効値の大きさだけを足すと成り立たないけど、複素数なら位相差も考慮できているから計算できるほうが自然だよねという感じです。

導出の流れは直流と全く同じです。一応、軽く流れを確認していきましょうか。二つの素子の直列、並列接続それぞれについて説明していきます。 二つが分かれば、それ以上になっても簡単に理解できます。

まず直列の場合です。素子1、素子2のインピーダンスをそれぞれ \(\dot{Z_1}, \ \dot{Z_2}\) とし、電流は \(\dot{I}\) で共通なので、 \[\dot{V} = \dot{V_1} + \dot{V_2} = \dot{I}\dot{Z_1}+\dot{I}\dot{Z_2} = \dot{I}(\dot{Z_1}+\dot{Z_2})\] が成り立つので、合成インピーダンスは \(\dot{Z_1} + \dot{Z_2}\) となりますね。

次に並列です。直列と同様に設定すると、 \[\frac{\dot{V}}{\dot{Z}} = \dot{I} = \dot{I_1} + \dot{I_2} = \frac{\dot{V}}{Z_1} + \frac{\dot{V}}{Z_2} = \dot{V}\left(\frac{1}{\dot{Z_2}}+ \frac{1}{\dot{Z_2}}\right)\] となり、合成インピーダンスは \(\frac{1}{\dot{Z_2}}+ \frac{1}{\dot{Z_2}}\) となります。

例題

それじゃあ、更に複雑な例題で、威力を実感してみましょうか。

例題：R,L,Cを含む複雑な回路

以下のような自己インダクタンス \(L\) のコイル、静電容量 \(C\) のコンデンサ、抵抗値 \(R\) の抵抗、\(V(t) = V_0\sin{\omega t}\) の交流電源を含む回路がある。 \(\omega L = \frac{1}{\omega C}\) であるとき、コイルに流れる電流の実効値を求めよ。

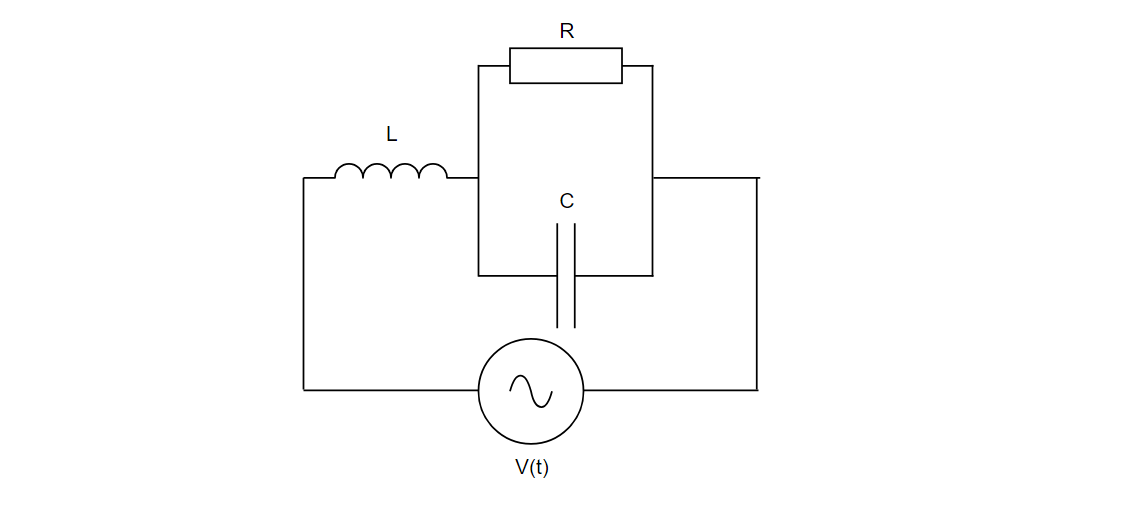
図4.RLCを含む複雑な回路

解答

電源電圧の複素ベクトル \(\dot{V}\) を \(V = \frac{1}{\sqrt{2}}V_0\) として、 \(\dot{V} = V\) とします。 最終的には全体の合成インピーダンスを求めていきたいですが、いきなり全体の合成インピーダンスを求めるのは難しいので、まずは、並列部分の合成インピーダンス \(\dot{Z'}\) を求めます。 \[\frac{1}{\dot{Z'}} = \frac{1}{R} + \frac{1}{\left(\frac{1}{j\omega C}\right)}\] であるので、 \[\dot{Z'} = \frac{R}{1 + jR\omega C}\] となります。 さらに、直流部分の合成抵抗も考えることで、全体の合成インピーダンス \(\dot{Z}\) は \[\dot{Z} = \dot{Z'} + j\omega L = \frac{R}{1 + jR\omega C} + j\omega L\] となります。分母分子に \(1 - jR\omega C\) をかけることで、有理化のようなことをして整理します。 \[\dot{Z} = \frac{R(1 - jR\omega C)}{1 + (R\omega C)^2} + \frac{j\omega L + jR^2\omega^3 LC^2}{1 + (R\omega C)^2} = \frac{R + j(\omega L + R^2\omega C(\omega^2 LC-1))}{1 + (R\omega C)^2}\] となります。ここで、\(\omega L = \frac{1}{\omega C}\) なので、\(\omega ^2LC = 1\) であり、これを用いて、 \[\dot{Z} = \frac{R + j\omega L}{1 + (R\omega C)^2}\] となります。

よって \[ \dot{I} = \frac{\dot{V}}{\dot{Z}}\] なので、電流の実効値、\(|\dot{I}|\) は、 \[|\dot{I}| = \frac{|\dot{V}|}{|\dot{Z}|} = \frac{V}{\left( \frac{\sqrt{R^2 + (\omega L)^2}}{1 + (R\omega C)^2} \right)} = \frac{1 + (R\omega C)^2}{\sqrt{2(R^2 + (\omega L)^2)}}V_0\] となり、四則演算だけで計算することができました。

演習問題

問題1：RLC直列回路

図のように、起電力 \(V_0\sin{\omega t}\) の交流電源、静電容量 \(C\) のコンデンサ、自己インダクタンス \(L\) のコイル、抵抗値 \(R\) の抵抗が直列に繋がれた回路がある。 このとき、抵抗での単位時間当たりの消費電力を求めよ。

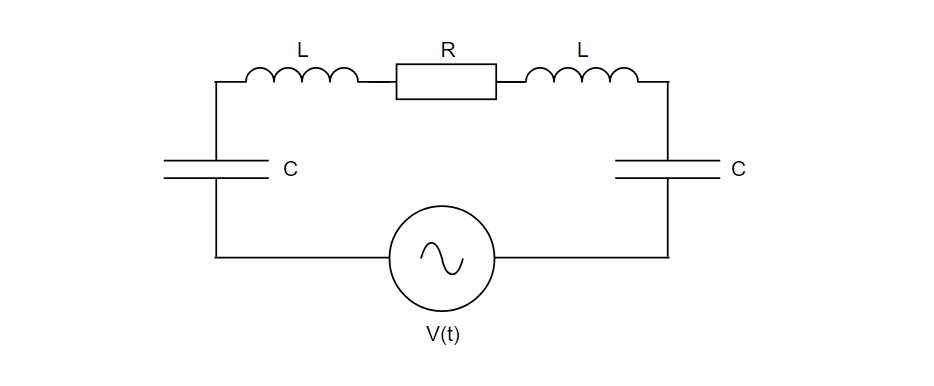
図5.RLCを含む複雑な回路

交流電源の起電力の向きはどちら向きでも結果に影響はないです。

余力があれば、消費電力を最大化するような \(\omega , L, C\) の条件も考えてみてください。

コイルとコンデンサが二つありますが、これは公式暗記マンだとやや苦しむかもしれません。 本質的には何も難しくないですね。

問題2：RLC並列回路

図のように、起電力 \(V_0\sin{\omega t}\) の交流電源、静電容量 \(C\) のコンデンサ、自己インダクタンス \(L\) のコイル、抵抗値 \(R\) の抵抗が並列に繋がれた回路がある。 このとき、抵抗、コイル、コンデンサでの単位時間当たりの消費電力を求めよ。

図6.RLC並列回路

どうですか？ほぼ機械的に解けてしまいましたね。

問題3：電流とインピーダンスが無関係になる条件(電験三種過去問)

図のように、起電力 \(V_0\sin{\omega t}\) の交流電源、静電容量 \(C\) のコンデンサ、自己インダクタンス \(L\) のコイル、抵抗値 \(R\) の抵抗が繋がれた回路がある。 このとき、抵抗、コイルの直列部分に流れる電流が、その合成インピーダンス \(\dot{Z}\) に無関係なる条件を求めよ。

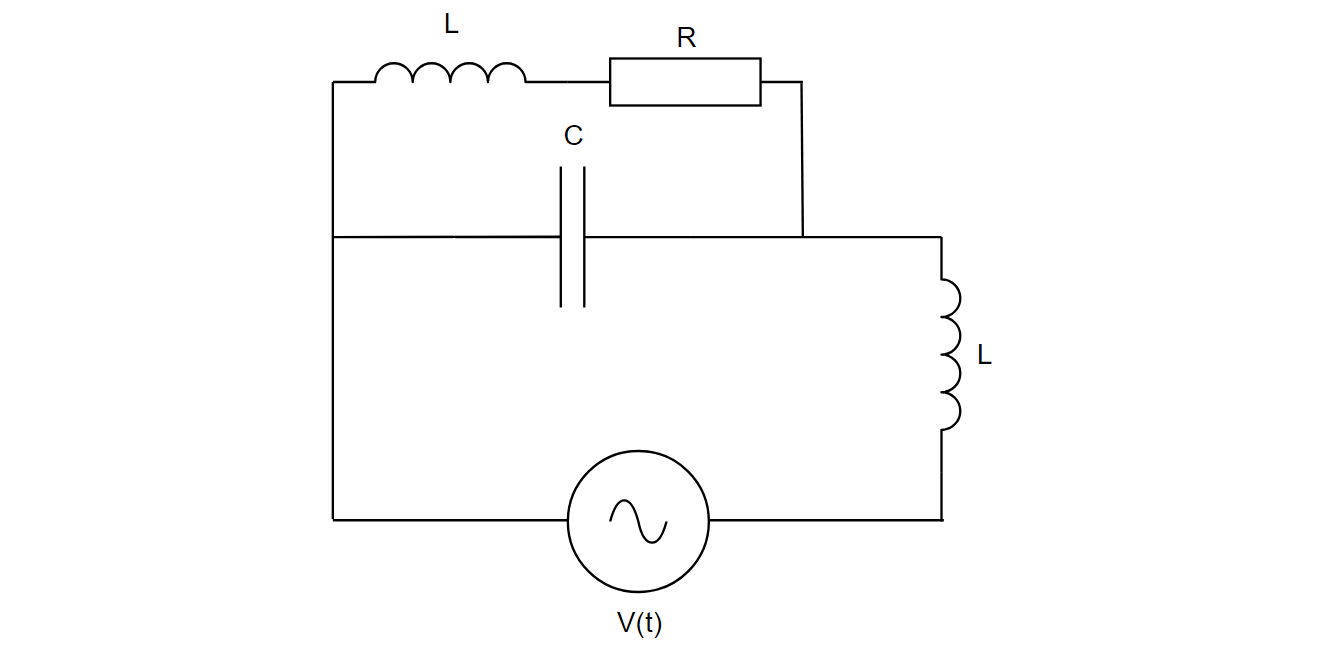
図7.RLCを含む複雑な回路

これは比較的難しい問題だと思います。何を言っているのかのイメージがわきにくいかもしれませんね。

問題4：電気振動への応用

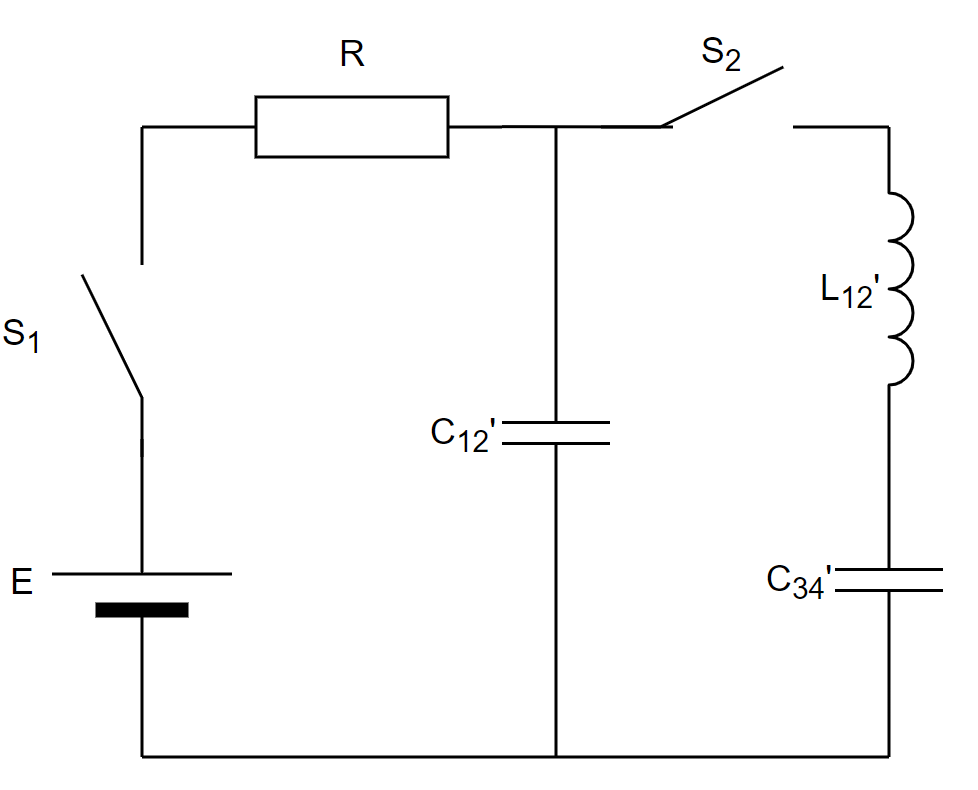
図のような起電力 \(E\) の電池、抵抗 \(R\) の抵抗1、静電容量 \(C_1,C_2,C_3,C_4\) のコンデンサ1,2,3,4、自己インダクタンス \(L_1,L_2\)、相互インダクタンス \(M\) のコイル1,2、スイッチ1,2を含む回路がある。 はじめ、スイッチ1,2は共に開いており、全てのコンデンサに電荷は蓄えられていなかった。 スイッチ1を閉じて十分に時間がたった後に、スイッチ1を開き、スイッチ2を閉じたところ電気振動が起こった。 この電気振動の周期を求めよ。ただし、\(M^2 < L_1L_2\) とする。

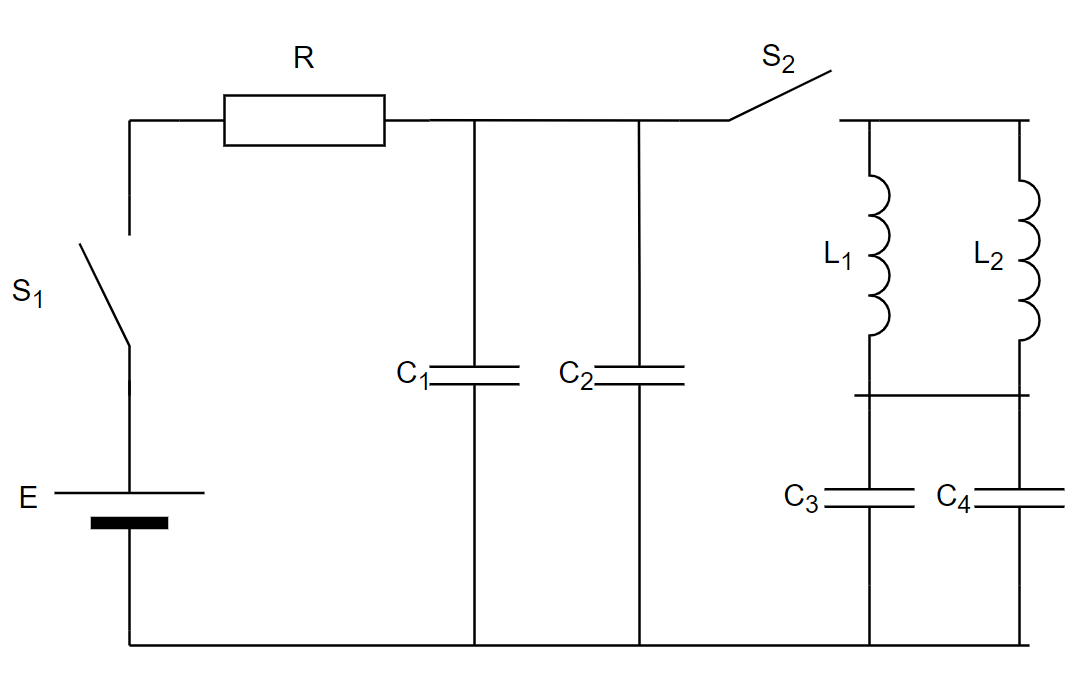
図8.電気振動への応用

これは物理の自作問題の一つです。出典はここです。普通に、交流以外の要素も難しいのですが、電気振動に交流の考え方が応用できるということを実感してほしいです。

コンデンサとコイルの合成を行うことで、右のような等価回路を得ます。

図9.等価回路

この合成後の静電容量 \(C_{12}',C_{34}'\) と自己インダクタンス \(L_{12}'\) を求めていきます。 コンデンサの合成に関しては、簡単で、 \[C_{12}'=C_1+C_2, \ C_{34}'=C_3+C_4\] となります。

次にコイルの合成を考えます。電流回路図下向きを正にしてコイル1に流れる \(I_1\) 、コイル2に流れる電流を \(I_2\) とします。 ここで、\(I_{12}'=I_1+I_2\) としておきます。電位差について考えることで \[ L_1\frac{\Delta I_1}{\Delta t} + M\frac{\Delta I_2}{\Delta t} = L_2\frac{\Delta I_2}{\Delta t} + M\frac{\Delta I_1}{\Delta t} \] を得ます。これより、以下を得ます。 \[ \frac{\Delta I_1}{\Delta t} =\frac{L_2-M}{L_1+L_2-2M} \frac{\Delta I_{12}'}{\Delta t}, \ \frac{\Delta I_2}{\Delta t} =\frac{L_1-M}{L_1+L_2-2M} \frac{\Delta I_{12}'}{\Delta t} \] 以上より、 \[ L_1\frac{\Delta I_1}{\Delta t} + M\frac{\Delta I_2}{\Delta t} = L_2\frac{\Delta I_2}{\Delta t} + M\frac{\Delta I_1}{\Delta t} = \frac{L_1L_2-M^2}{L_1+L_2-2M}\frac{\Delta I_{12}'}{\Delta t} \] です。よって、合成インダクタンス \(L_{12}'\) は以下のようになります。これはAM-GMなどから正であることがわかります。 \[L_{12}'=\frac{L_1L_2-M^2}{L_1+L_2-2M}\]

右の回路の電気振動を求めていきます。 \(C_{12}',C_{34}',L_{12}'\) として計算し、最後に代入していきます。 ここで各パラメータは以下のとおりです。 \[C_{12}'=C_1+C_2, \ C_{34}'=C_3+C_4, \ L_{12}'=\frac{L_1L_2-M^2}{L_1+L_2-2M}\]

図9(再掲).等価回路

電気振動で交流電流が流れるとみなして、キルヒホッフの法則を適用します。 コンデンサ1,2、コイル1のインピーダンスはそれぞれ \[\frac{1}{j \omega C_{12}'}, \ \frac{1}{j \omega C_{34}'}, \ j \omega L_{12}'\] であるから、流れる電流を \(\dot{I}\) として、キルヒホッフの法則より、 \[ -j\dot{I}\frac{1}{\omega C_{12}'} - j\dot{I}\frac{1}{\omega C_{34}'} + j\dot{I}\omega L_{12}' = 0 \] を得ます。\(\dot{I}\) は \(0\) ではないので、 \[ -\frac{1}{\omega C_{12}'} - \frac{1}{\omega C_{34}'} + \omega L_{12}' = 0 \] を得ます。よって、 \[\omega = \sqrt{\frac{C_{12}'+C_{34}'}{L_{12}'C_{12}'C_{34}'}}\] となり、周期 \(T\) は \[T = 2\pi \sqrt{\frac{L_{12}'C_{12}'C_{34}'}{C_{12}'+C_{34}'}}\] とります。最後に、各パラメータを与えられた文字で表して、 \[T = 2\pi \sqrt{\frac{(L_1L_2-M^2)(C_1+C_2)(C_3+C_4)}{(L_1+L_2-2M)(C_1+C_2+C_3+C_4)}}\] とります。