多重総和記号の計算

今回は通常では計算することができないような多重総和記号の式を簡単に解く方法を皆さんにお伝えしていきたいと思います。 必要な前提知識はほぼゼロです。それでは、よろしくお願いします。

定理

シンプルな式ではありますが、地味に手が付けにくい問題です。 こういった多重総和記号の式はお互いのシグマが絡み合っているので教科書的には解くことができません。

式が複雑なので、イメージを掴むために例を提示しておきます。 シグマを連ねて書くと長くなるので、 \[f_{j}\left(i\right)=\sum_{a_{1}=1}^{i}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{j}=1}^{a_{j-1}}a_{j}\] のように \(f_{j}(i)\) を定義します。 \[f_{1}(4)=1+2+3+4, \ f_{2}(4)=(1)+(1+2)+(1+2+3)+(1+2+3+4) \] \[f_{3}(4)=\{(1)\}+\{(1)+(1+2)\}+\{(1)+(1+2)+(1+2+3)\}+\{(1)+(1+2)+(1+2+3)+(1+2+3+4)\}\] といった具合になっています。

証明1

こちらの恒等式を利用していきます。

証明

望遠鏡和を使えばいいだけなので、省略します。\(\blacksquare\)

名前の由来は、パスカルの三角形上でこの公式を考えるとホッケースティックに似ているからだったはずです。

証明

補題から、 \[\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}{_{a_{m}}C_{1}}=\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m-1}=1}^{a_{m-2}}{_{a_{m-1}+1}C_{2}}=\sum_{a_{1}=1}^{n}{_{n+m-1}C_{m}}=_{n+m}C_{m+1}=_{n+m}C_{n-1} \] のように変形できるので題意は示された。\(\blacksquare\)

証明2

証明

\[ \sum_{a_{1}=1}^{n-1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}a_{m}=\sum_{a_{1}=1}^{n-1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m}=1}^{a_{m-1}}a_{m}+\sum_{a_{1}=1}^{n}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{m-1}=1}^{a_{m-2}}a_{m-1} \\ \] である。 また、任意の正整数 \(k\) に対し、 \[\sum_{a_{1}=1}^{1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{k}=1}^{a_{k-1}}a_{k}=1\] と、 \[\sum_{a_{1}=1}^{k}{a_1} = _{k+1}C_2\] が成り立つゆえ、求める式は原点から \((n-1,m+1)\) へ一度も引き返さずにいくような場合の数と等しい。 したがって、\((与式)=_{n+m}C_{n-1}\) である。題意は示された。\(\blacksquare\)

解説

これは組み合わせ論的に考察しています。

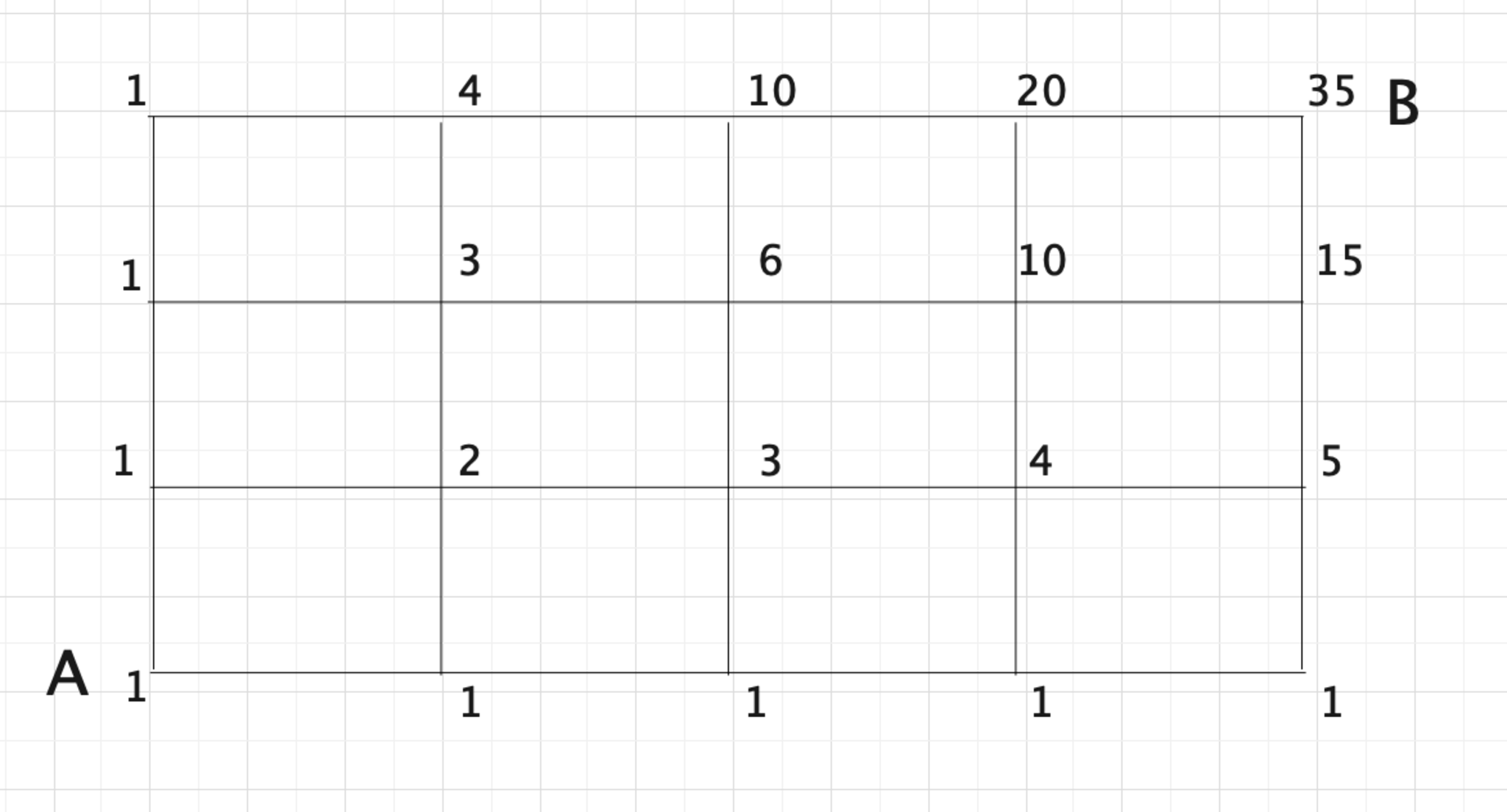
図1.中学入試などでよく見るアレ

\(2\) 以上の任意の正整数 \(i,j\) に対して \(f_{j}(i)=f_{j-1}(i)+f_{j}(i-1)\) が成立し、ついでに、自明なケースについて、 \[\sum_{a_{1}=1}^{1}\sum_{a_{2}=1}^{a_{1}}\cdots\sum_{a_{k}=1}^{a_{k-1}}a_{k}=1\] \[\sum_{a_{1}=1}^{k}{a_1} = _{k+1}C_2\] が成立していて、上の画像にあるような道のりの数え上げのように計算することができます。 そして、これは同時に二項係数でも表すことができたので、上のようになるわけです。

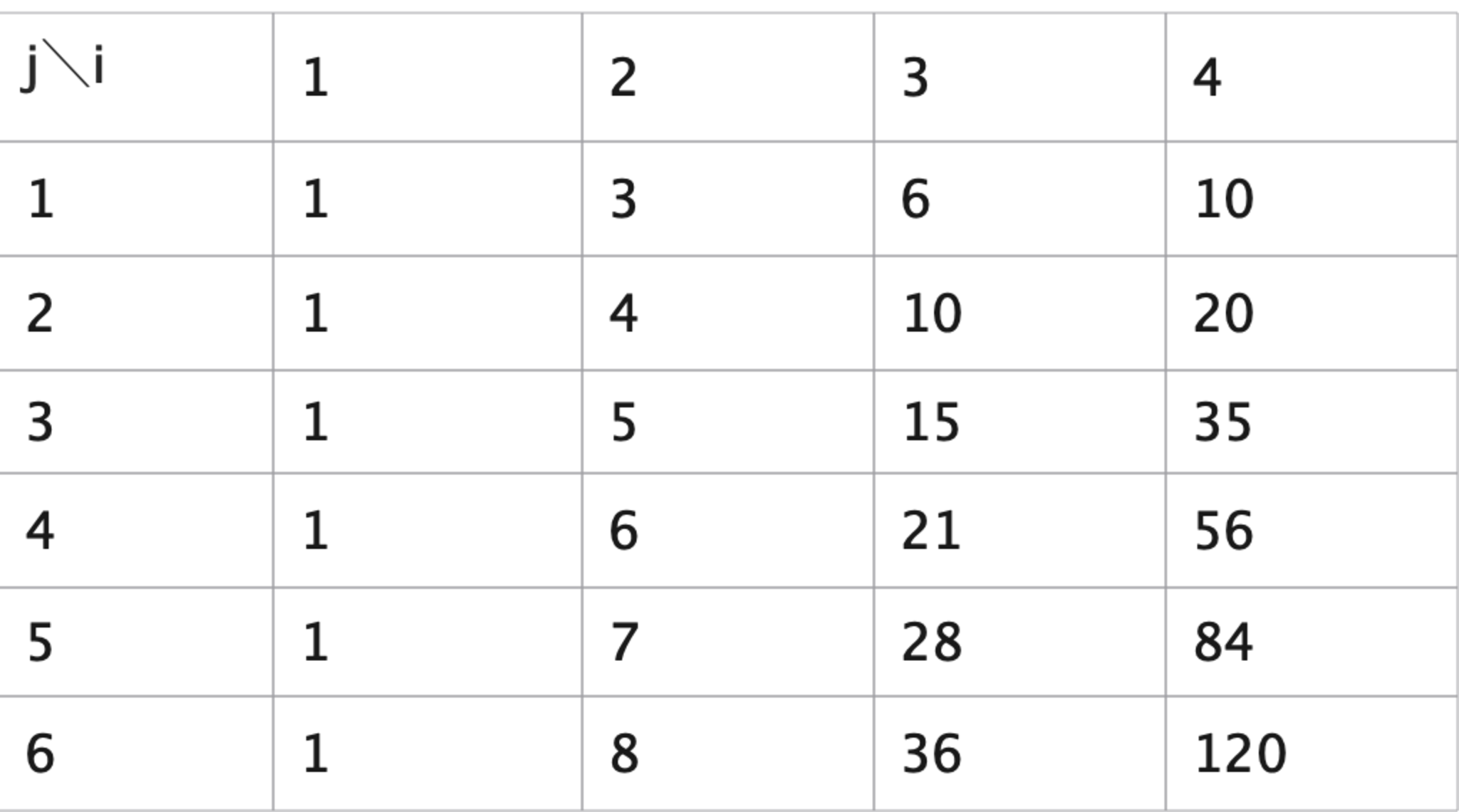
図2.表にしてみる

こんな感じで、表にして足し合わせたらわかりやすいかもです自明なケースが、1行目とか1列目に対応していて、 \(f_{j}(i)=f_{j-1}(i)+f_{j}(i-1)\) という等式で右へ、下へと帰納的に計算できるという感じですね。