類似中線関連の構図 (Symmedian)
今回は、類似中線(Symmedian)という初等幾何においての重要な構図を解説していきます。 この記事の内容の半分くらいは、演習問題に詰まっていますのでぜひ最後まで読んでください。 この記事の作成にあたって、翁さんには大変お世話になりました。ありがとうございます!! それでは、よろしくお願いします。
定義
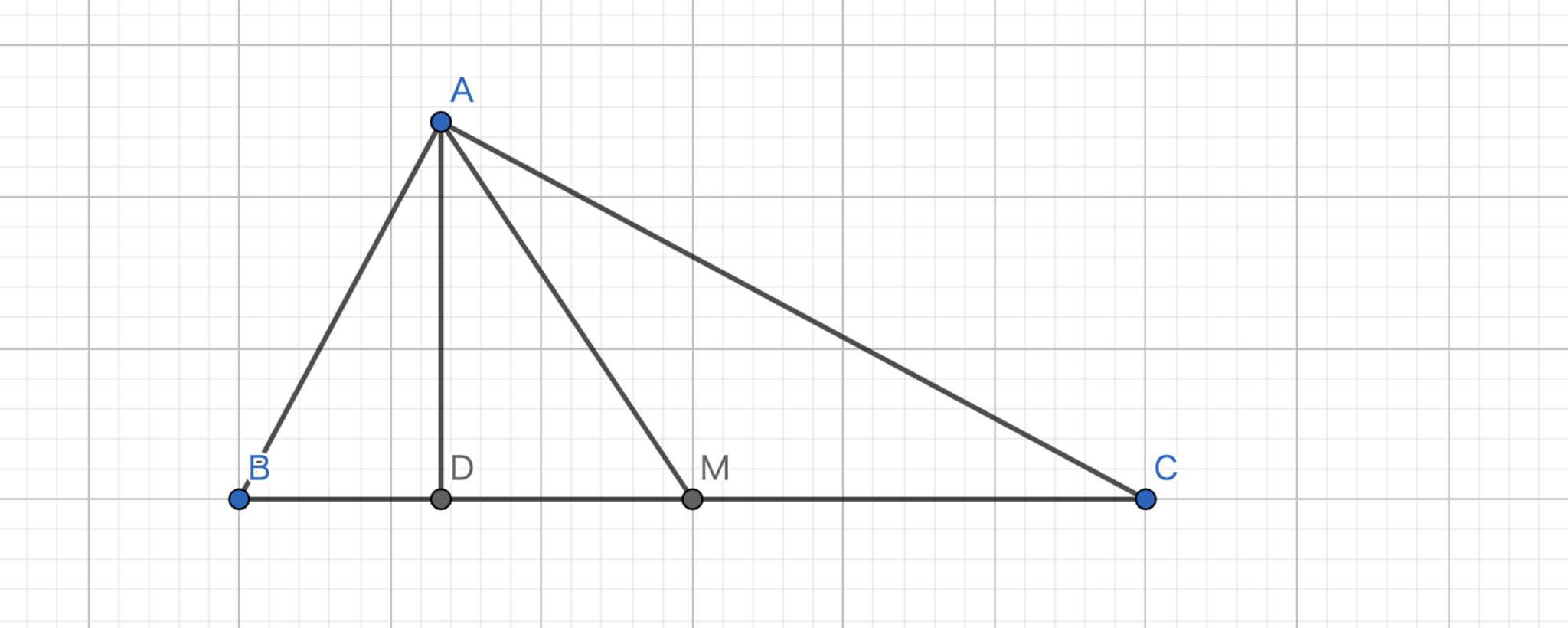
中線の等角共役線を類似中線と呼ぶ。 図において、\(AM,AD\) はそれぞれ中線と類似中線であり、\(\angle{BAM}=\angle{CAD}\) である。
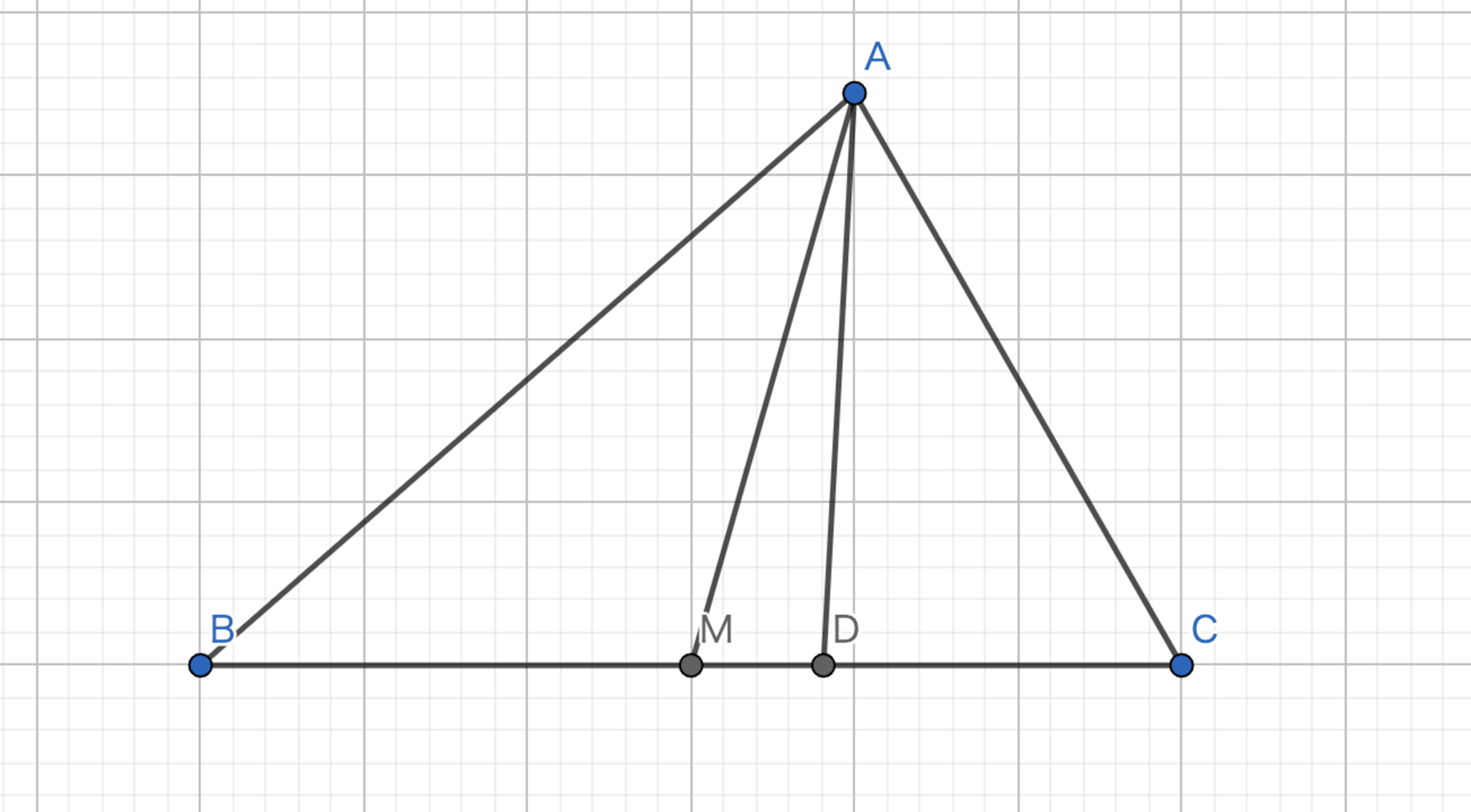
図1.類似中線 -定義
単純な定義ですが、想像しているよりも遥かに多くの面白い事柄があります。 個人的に、類似中線よりもSymmedianのほうが呼びなれているので、以下ではSymmedianと呼びます。 Symmedianは一つの三角形に対して、三つ存在するので、それらをA-Symmedianなどと呼んで区別します。
基本性質
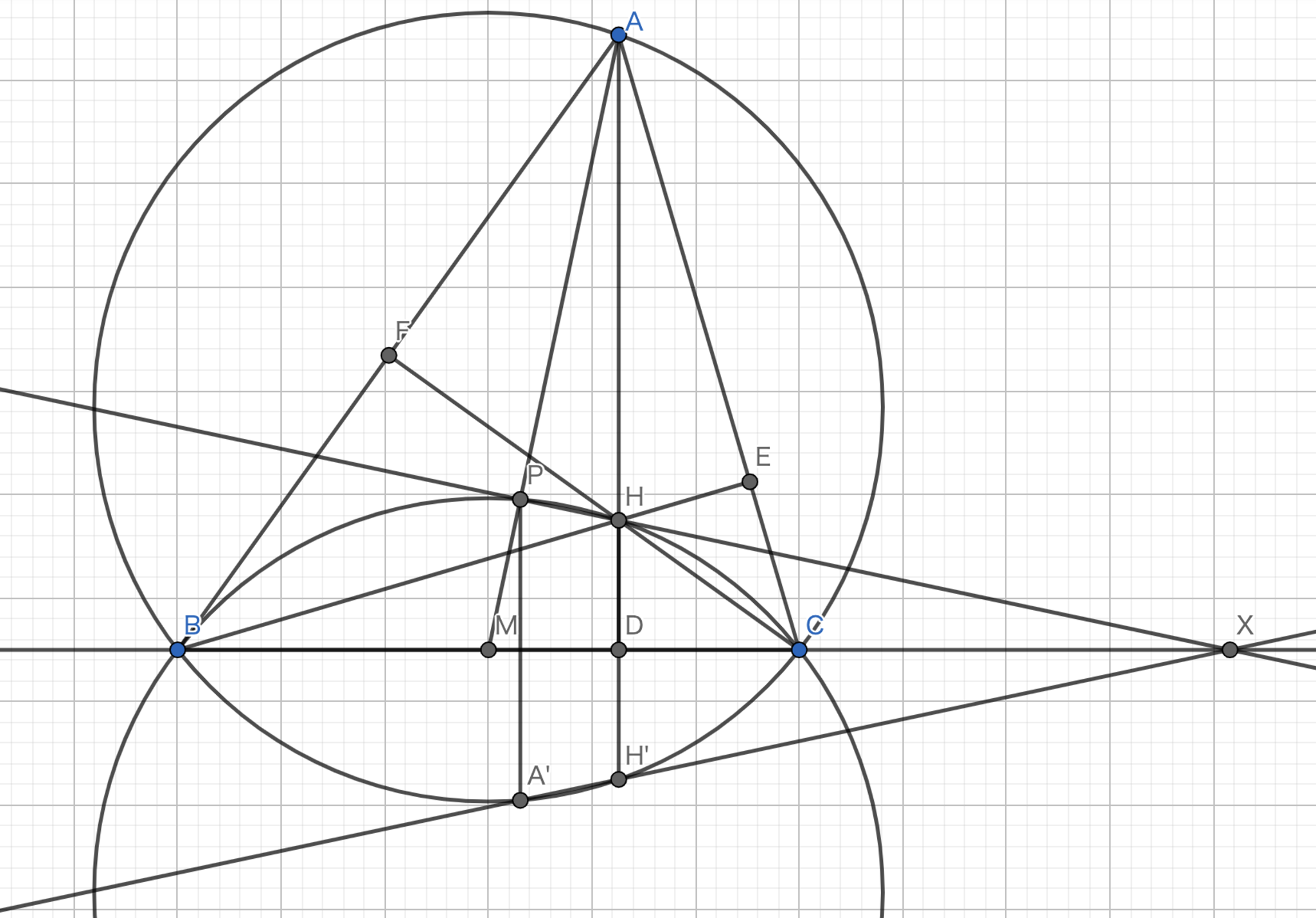
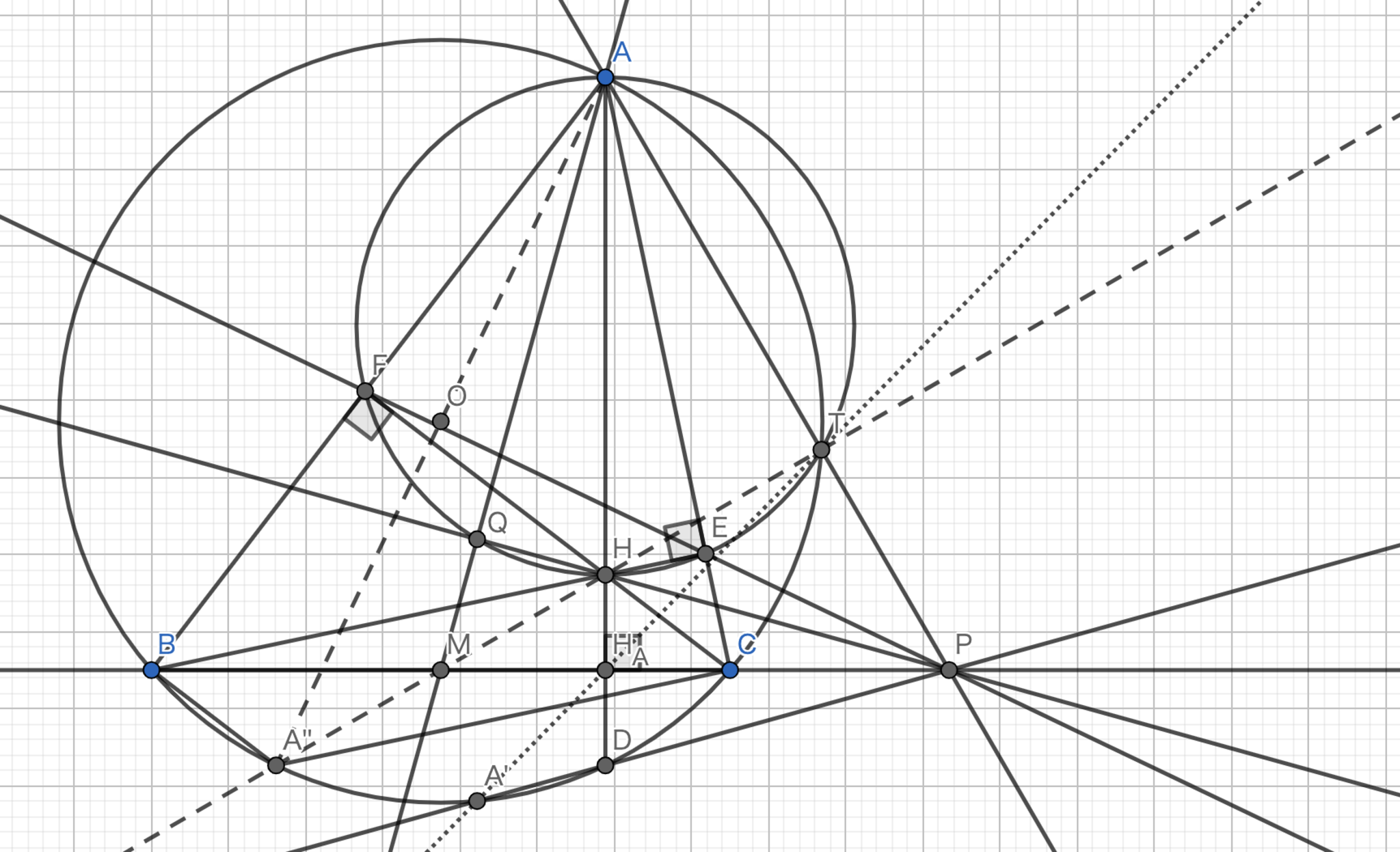
三角形 \(ABC\) の外接円の \(B,C\) における接線の交点を \(P\) とすれば \(AP\) は三角形 \(ABC\) のA-Symmedianとなる。
良い練習問題になると思うので知らない人は一度自分で考えてみてください!!
証明
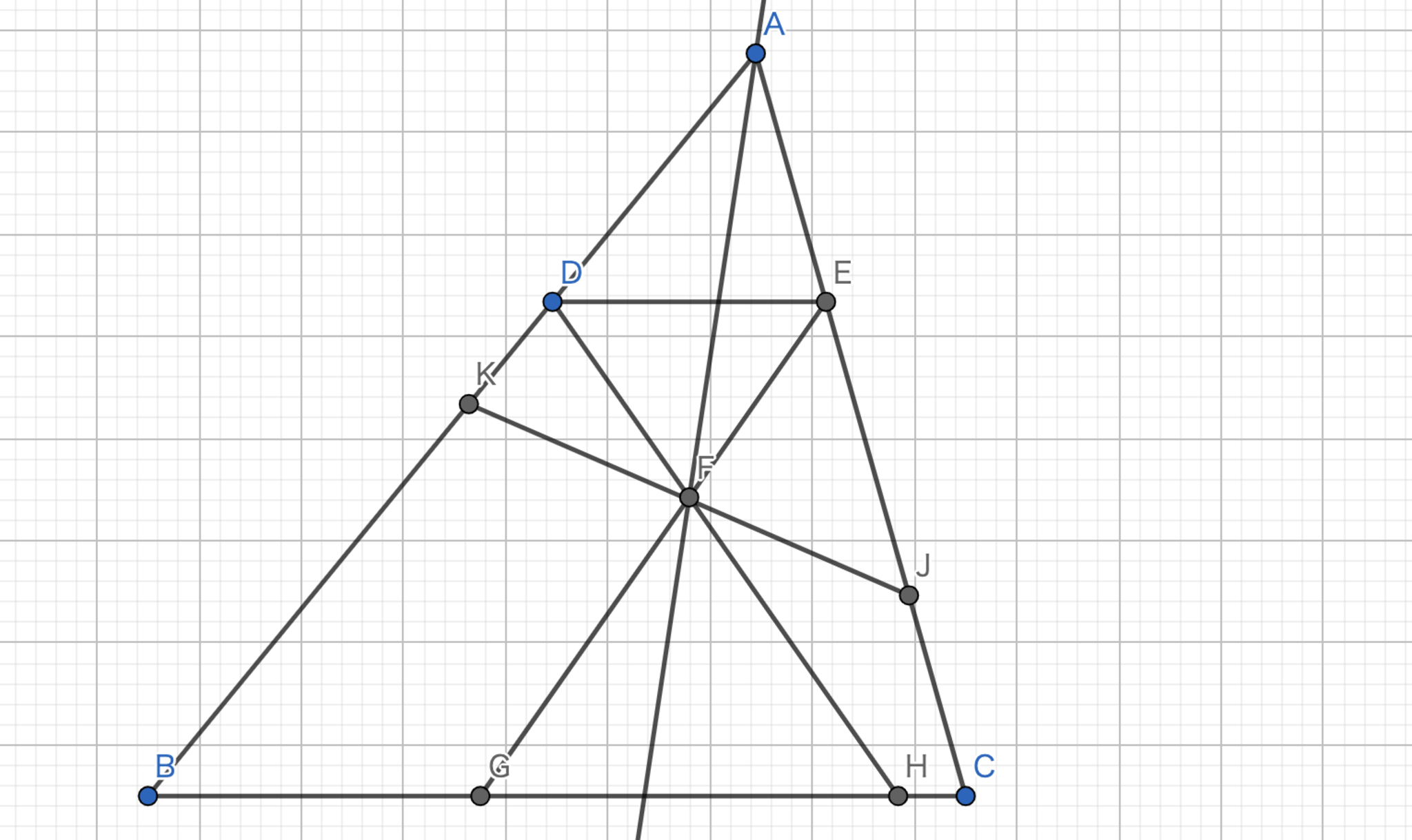
方針:三角形 \(ABD\) と三角形 \(AMC\) の相似を示す。
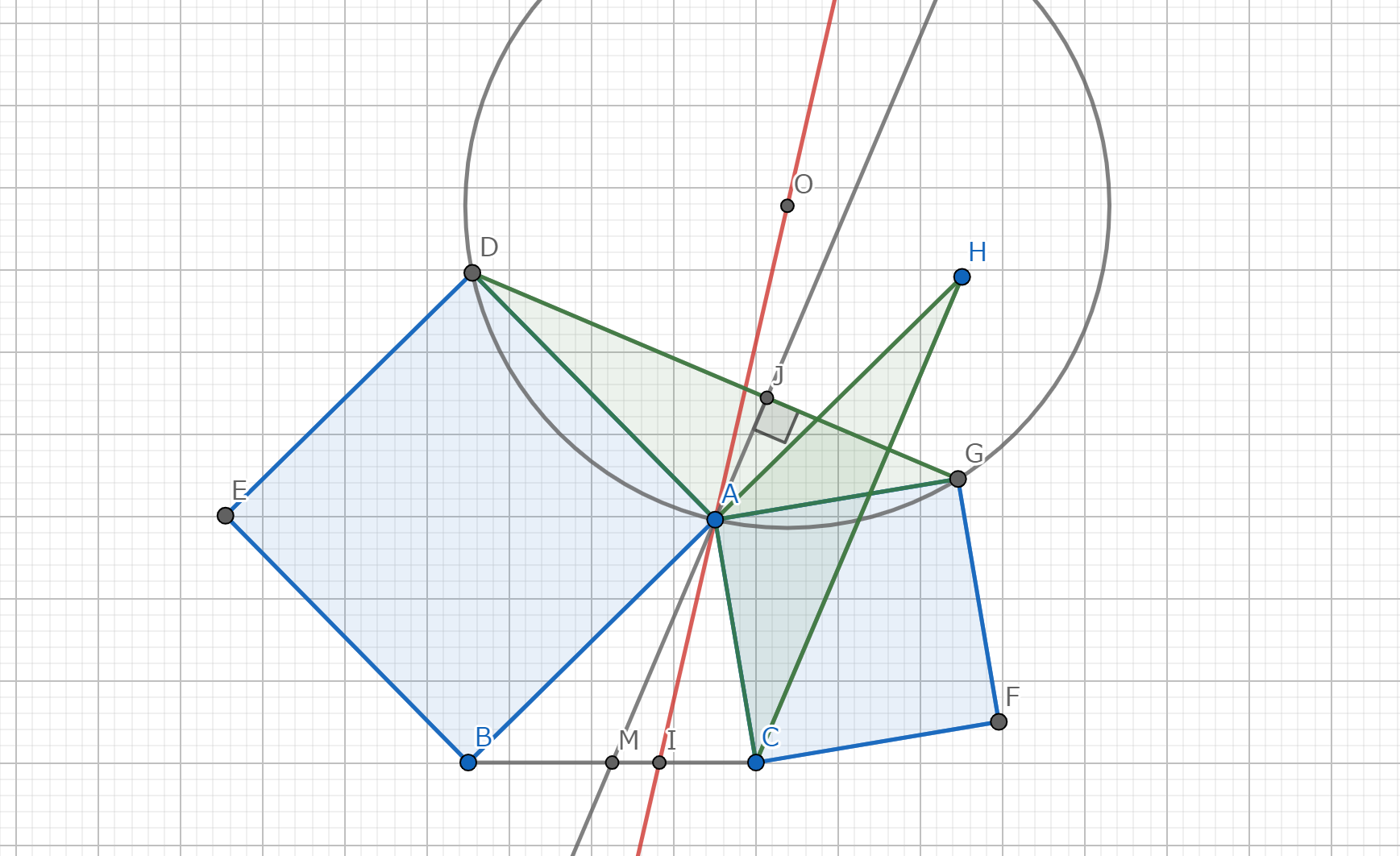
\(M\) を \(BC\) の中点、 \(H\) を \(AD\) の中点とする。 \(\angle{OBP}=\angle{OCP}=90°\) より、4点 \(O,B,P,C\) は共円である。 また、中心と弦への中点を結ぶ直線と弦は垂直に交わるから \(\angle{OHA}=90°\) である。 したがって、 \(B,P,C,H,O\) は共円である。 これより、 \(\angle{CHP}=\angle{COP}=\angle{BAC}\) がしたがう。 また、 \(\angle{BHD}=\angle{BAC}\) も得られる。 一方で、円周角の定理より、 \(\angle{BDH}=\angle{BCA}\) である。 以上より、 \(\triangle{ABC} \backsim \triangle{HBD}\) である。 このことから、 \( BD : DH = BC : CA \) が得られる。 さらに、 \(H\) が \(AD\) の中点、 \(M\) が \(BC\) の中点であることを利用すると、 \( BD : DA = MC : CA \) が得られる。 \(\angle{BDA}=\angle{MCA}\) より、 \(\triangle{ABD} \backsim \triangle{AMC}\) となる。 したがって、 \(AP\) はA-Symmedianである。 \(\blacksquare\)
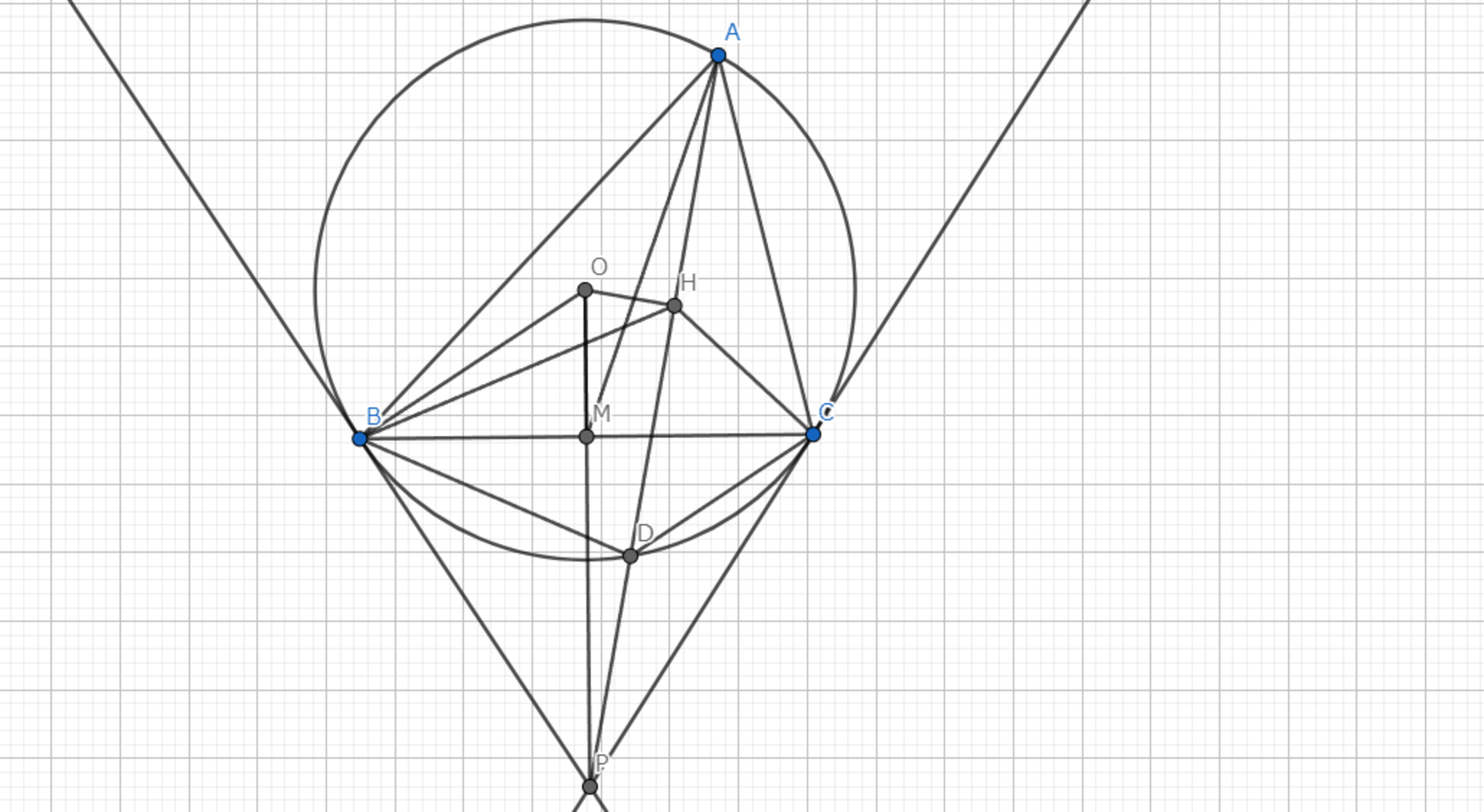
図2.定理1 -証明
Symmedianを作図したいときにも使えますし、自然に問題の中に出てくることもあります。 かなり基本的で大切な構図です。
ついでに...
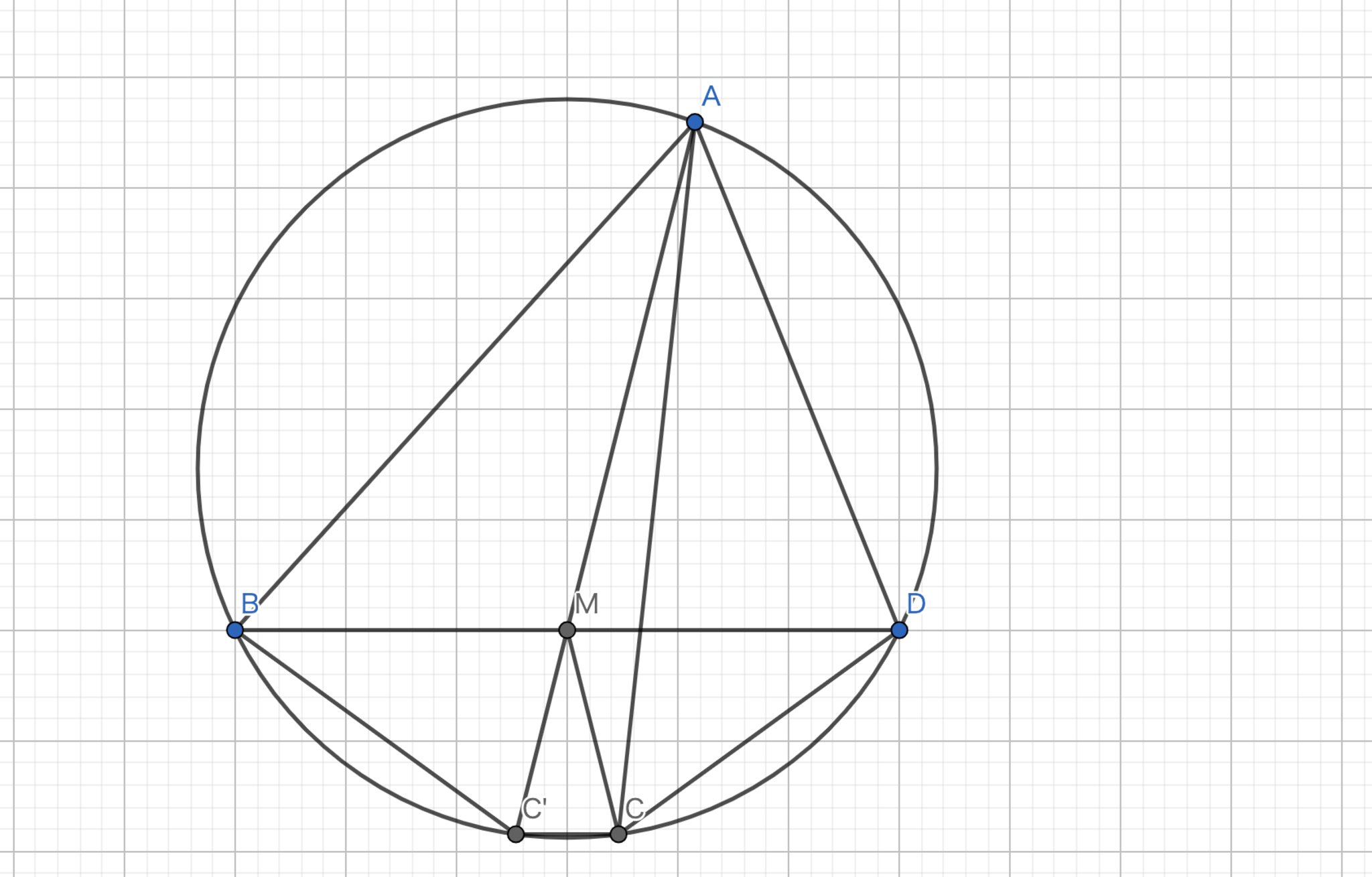
外心を \(O\) とする三角形 \(ABC\) のA-Symmedianと外接円の交点のうち、\(A\) でないものを \(D\) とするとき、 \(AD\) の中点 \(H\) として、\(H\) は三角形 \(OBC\) の外接円上にある。
証明
上の定理1の証明において、示した。\(\blacksquare\)
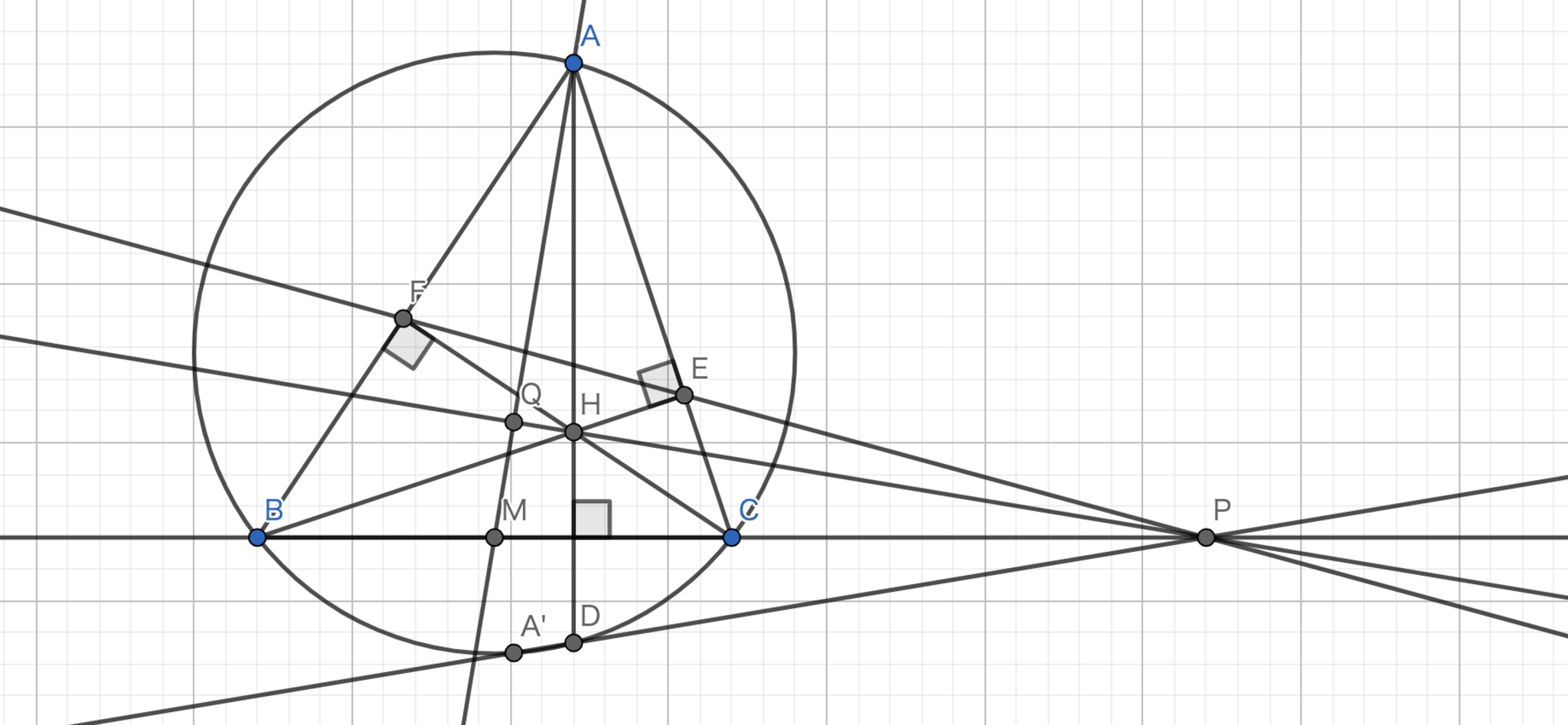
三角形 \(ABC\) の外接円の \(A\) における接線と直線 \(BC\) との交点を \(K\) とする。 \(K\) から三角形 \(ABC\) の外接円へ引いた接線との接点のうち \(A\) でないものを \(D\) とすると、\(AD\) はA-Symmedianである。
複数通りの証明がありますが、今回はせっかくなので定理1を活用していきます。
証明
方針:定理1と同様の手法を用いる。
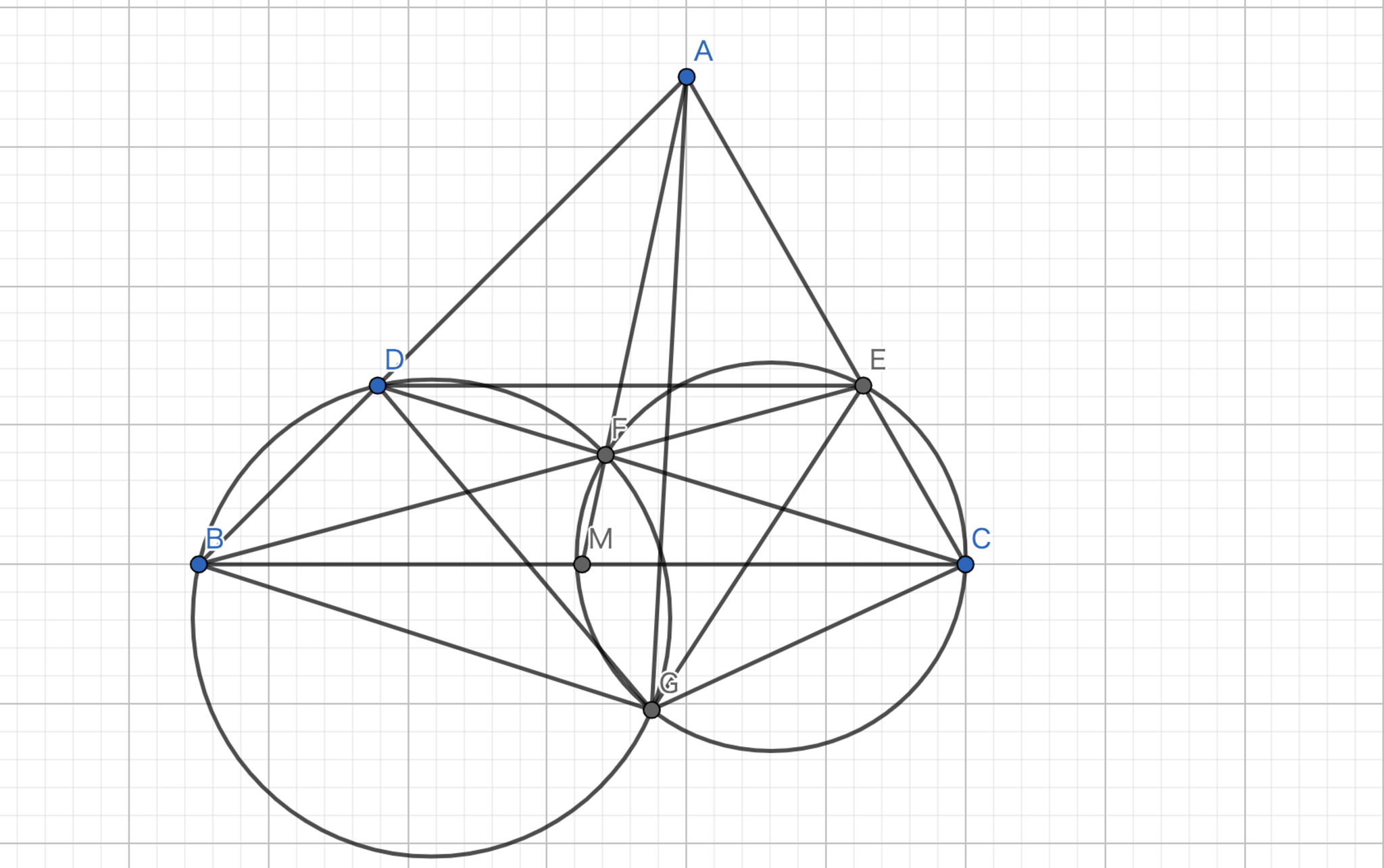
定理1より、\( BK \)は三角形\( BDA \)のB-Symmedianである。 したがって、\( \angle ABC = \angle HBD \) である。 また、円周角の定理より、\( \angle BCA = \angle BDH \) である。 よって、\( \triangle ABC \backsim \triangle HBD \) が従う。 \( BD : DH = BC : CA \) が得られる。 また、\( M, H \) が中点であることより、定理1の証明と同様に、\( \triangle ABD \backsim \triangle AMC \) である。 したがって、\( AD \) はA-Symmedianである。 \(\blacksquare\)
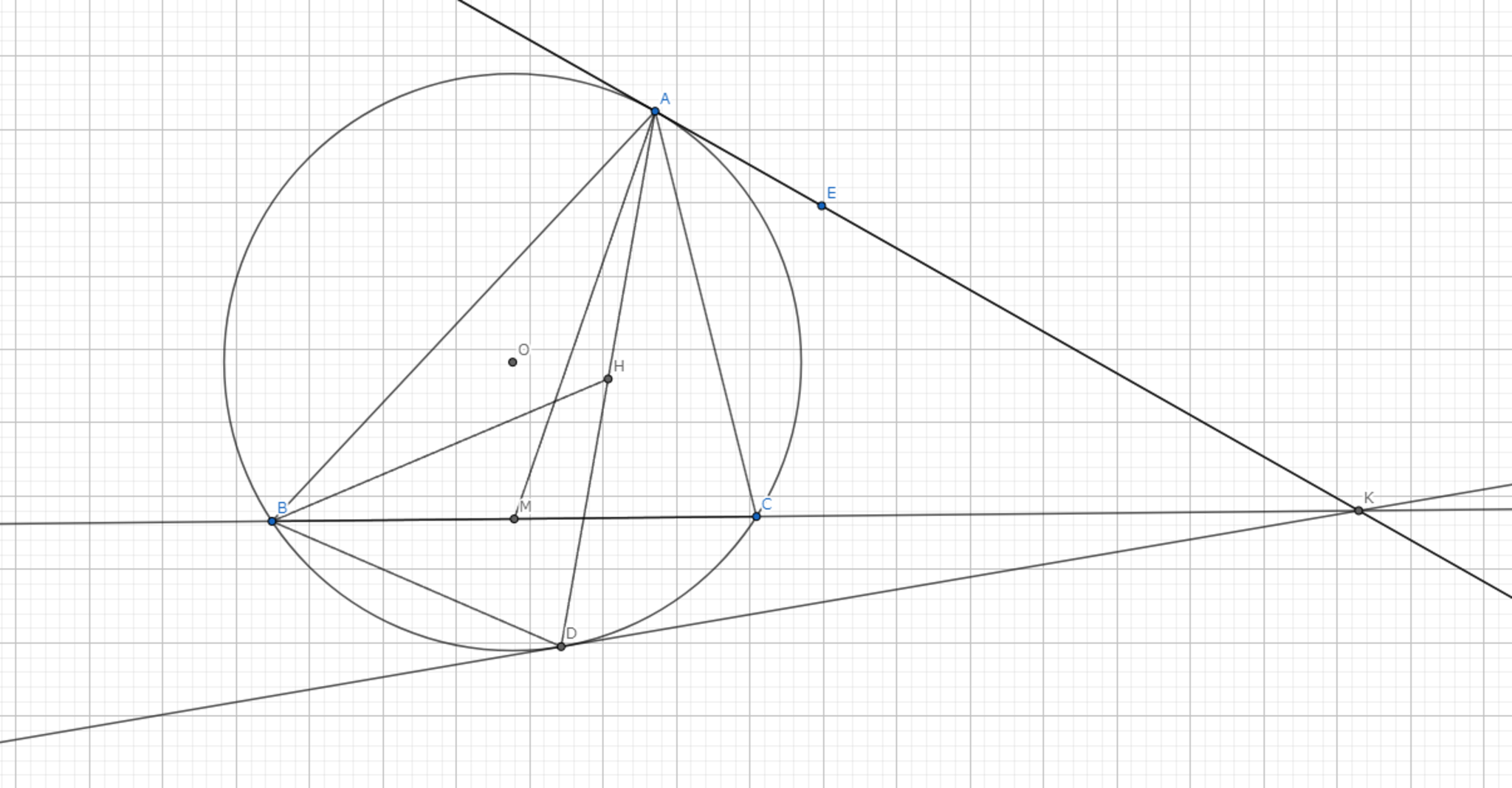
図3.定理3 -証明
三角形 \(ABC\) のA-Symmedianと外接円の交点のうち、\(A\) でないものを \(D\) とするとき、 \(AD\) の中点 \(H\) として、\(\angle{BHD} = \angle{CHD}\) である。
証明
定理2から、五点 \(B,C,O,H,P\) は共円ゆえ、簡単な角度計算より、\(\angle{BHP}=\angle{CHP}\) である。 \(\blacksquare\)
Steiner's ratio theorem と逆平行
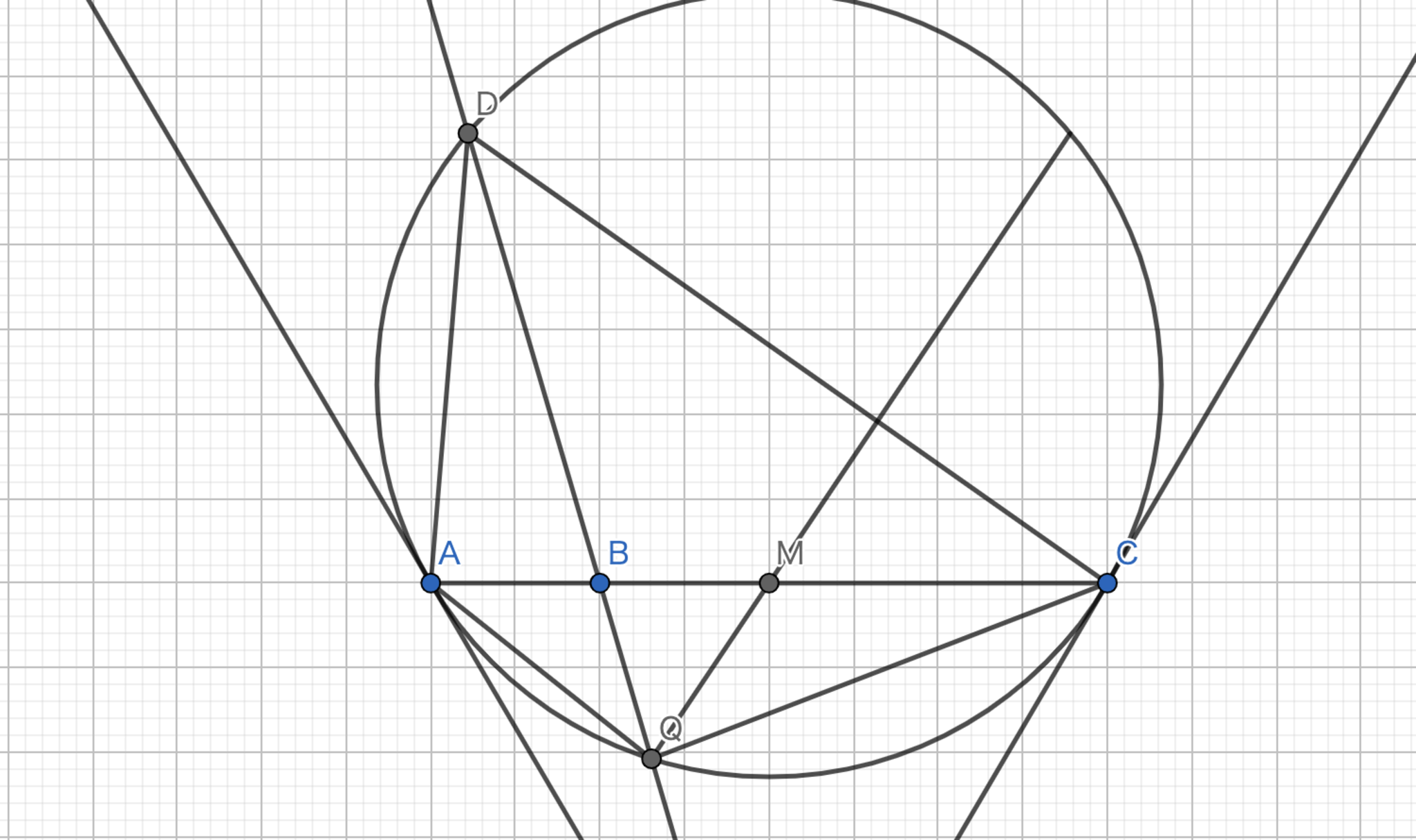
三角形 \(ABC\) のA-Symmedian上に点 \(G\) をとり、\(G\) から、直線 \(AB,AC\) におろした垂線の足を \(H,I\) とするとき、 \(GH:GI = AB:AC\) が成り立つ。
証明
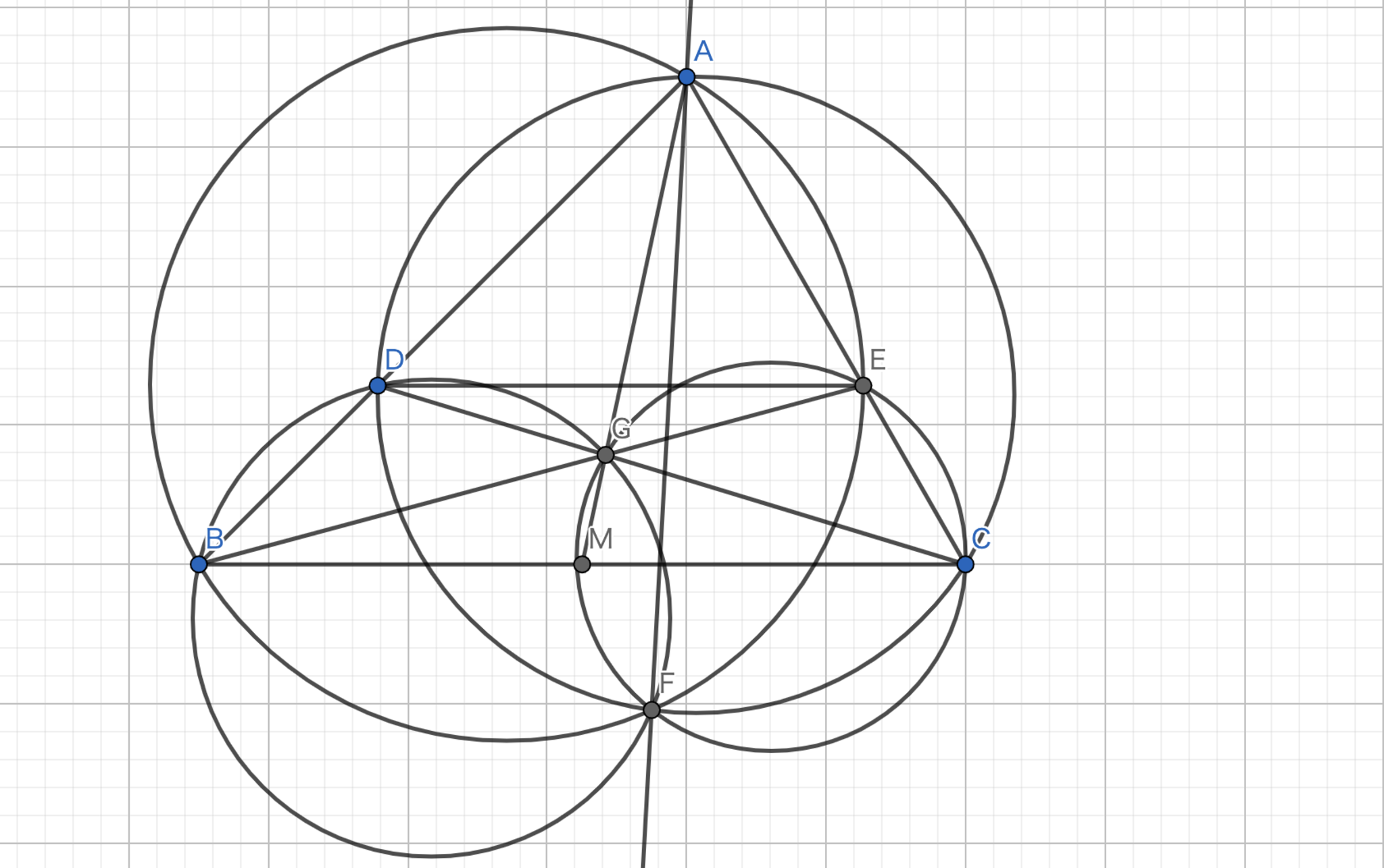
\(BC\) の中点を \(M\) とし、\(M\) から直線 \(AB,AC\) へとおろした垂線の足を \(E,F\) とする。 また、A-Symmedianと \(BC\) の交点を \(D\) とする。 \( AD \) はA-Symmedianであるから、\( \triangle AGI \backsim \triangle AME \)、 \( \triangle AGH \backsim \triangle AMF \)である。 よって、\( GH : GI = MF : ME \)が得られる。 \( M \)は中点なので、\( \triangle ABM = \triangle ACM \)。 したがって、\( AB \cdot EM = AC \cdot FM \) であり、これは \( MF : ME = AB : AC \) を意味する。 \(\blacksquare\)
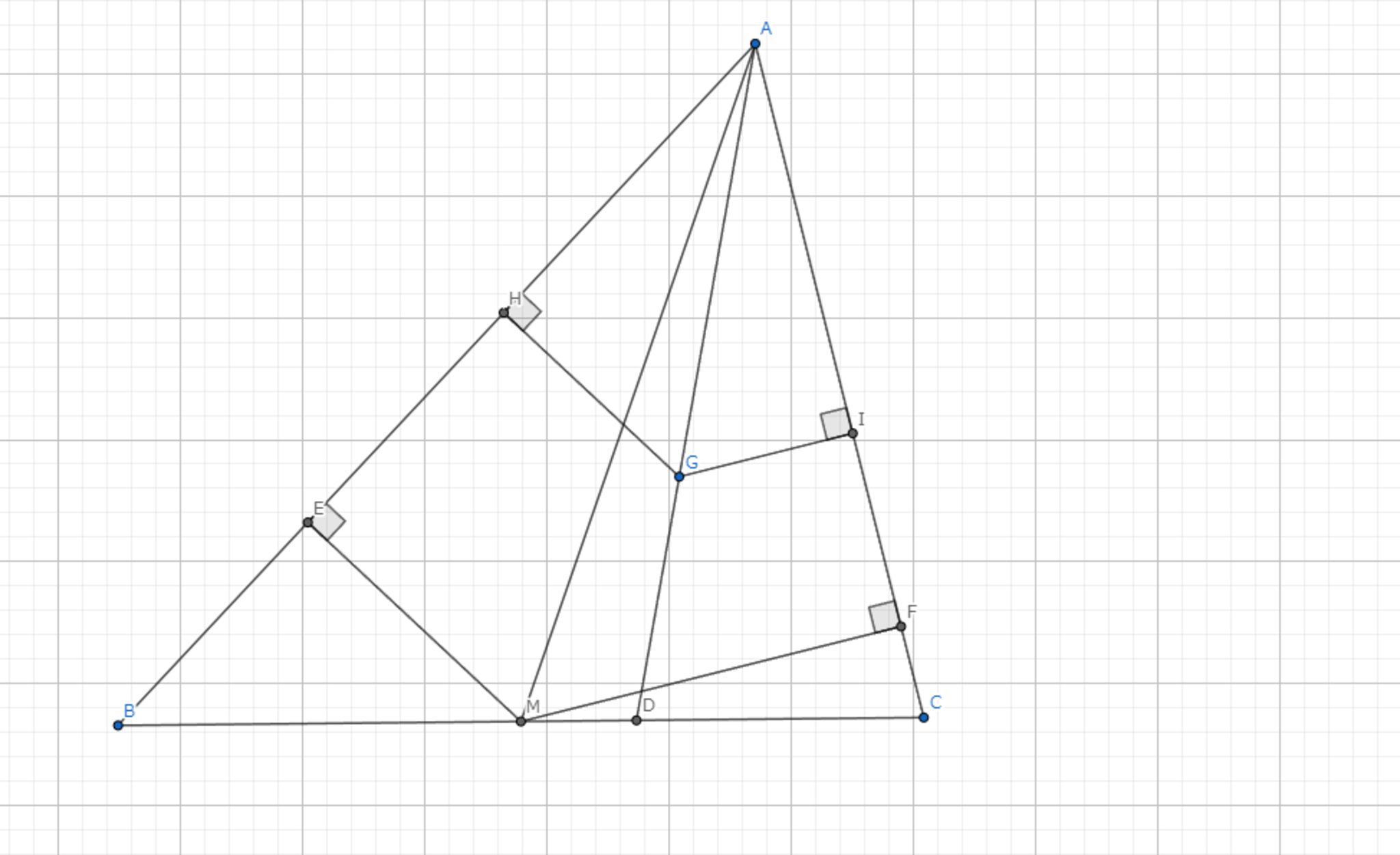
図4.定理5 -証明
三角形 \(ABC\) において、A-Symmedianと \(BC\) の交点を \(D\) とするとき、\(BD:CD=AB^2:AC^2\) が成り立つ。
証明
\( BD : CD =\triangle{ABD}:\triangle{ACD}= AB \cdot DF : AC \cdot DE \)。 ここで、定理5より、\( DF : DE = AB : AC \)である。 したがって、\( BD : CD = AB ^2: AC ^2\) である。 \(\blacksquare\)
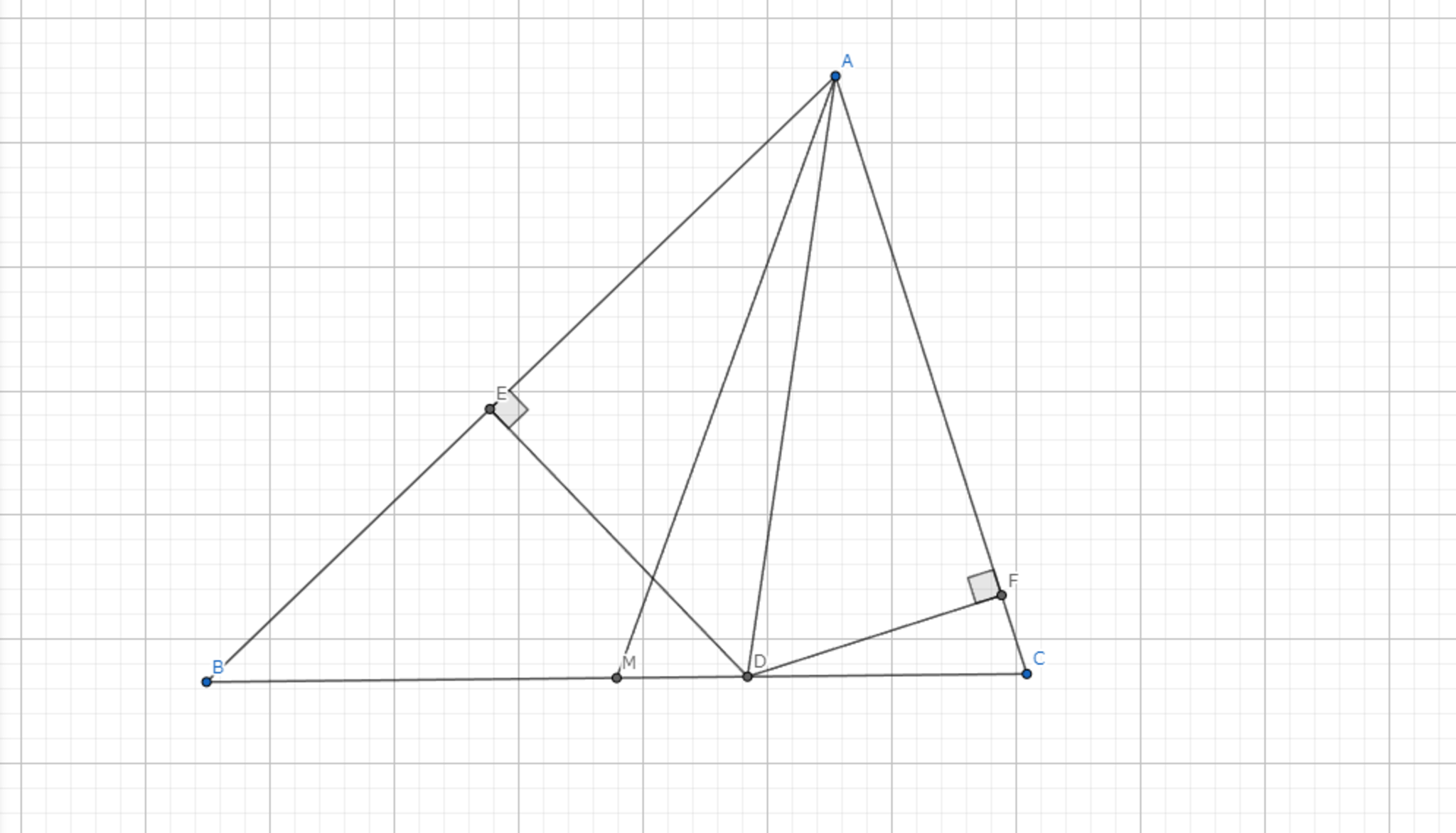
図5.定理6 -証明
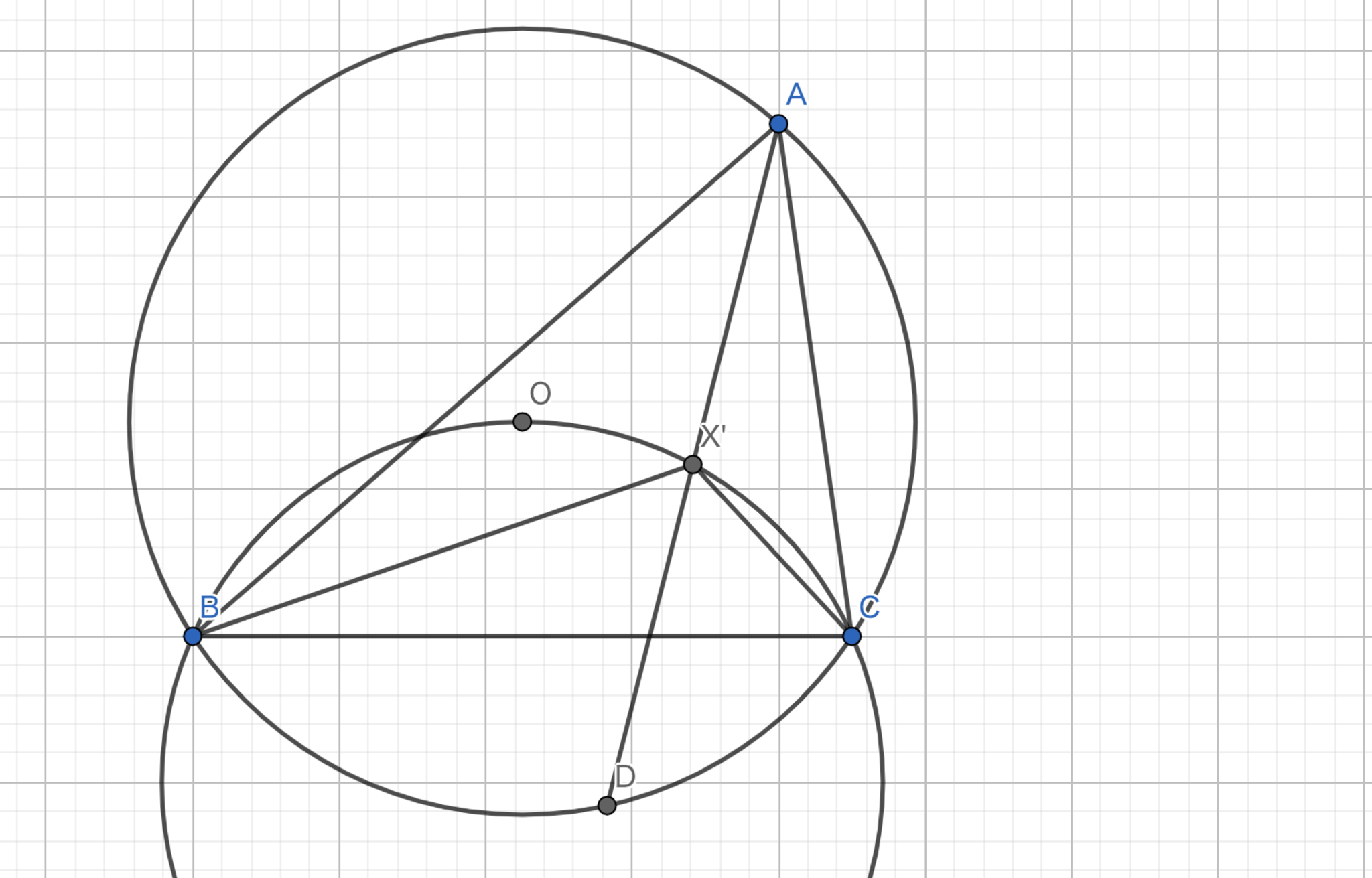
三角形 \(ABC\) のA-Symmedianは \(BC\) の逆平行線の中線である。
逆平行とは簡単に言うと、\(\angle{ABC}=\angle{AFE}\) となるような状況のことを言います。
証明
\(BC\)と\(EF\)は逆平行なので\(\angle{ABC}=\angle{AFE}\)、\(\angle{ACB}=\angle{AEF}\)である。 したがって、\(\triangle{ABC} \backsim \triangle{AFE}\)である。 また、\(AD\)がA-Symmedianなので\(\angle{EAN}=\angle{CAM}\)であるから\(\triangle{ACM} \backsim \triangle{AEN}\)である。 \( BC : MC = FE : NE =2:1\)であるから\(N\)は\(FE\)の中点である。 \(\blacksquare\)
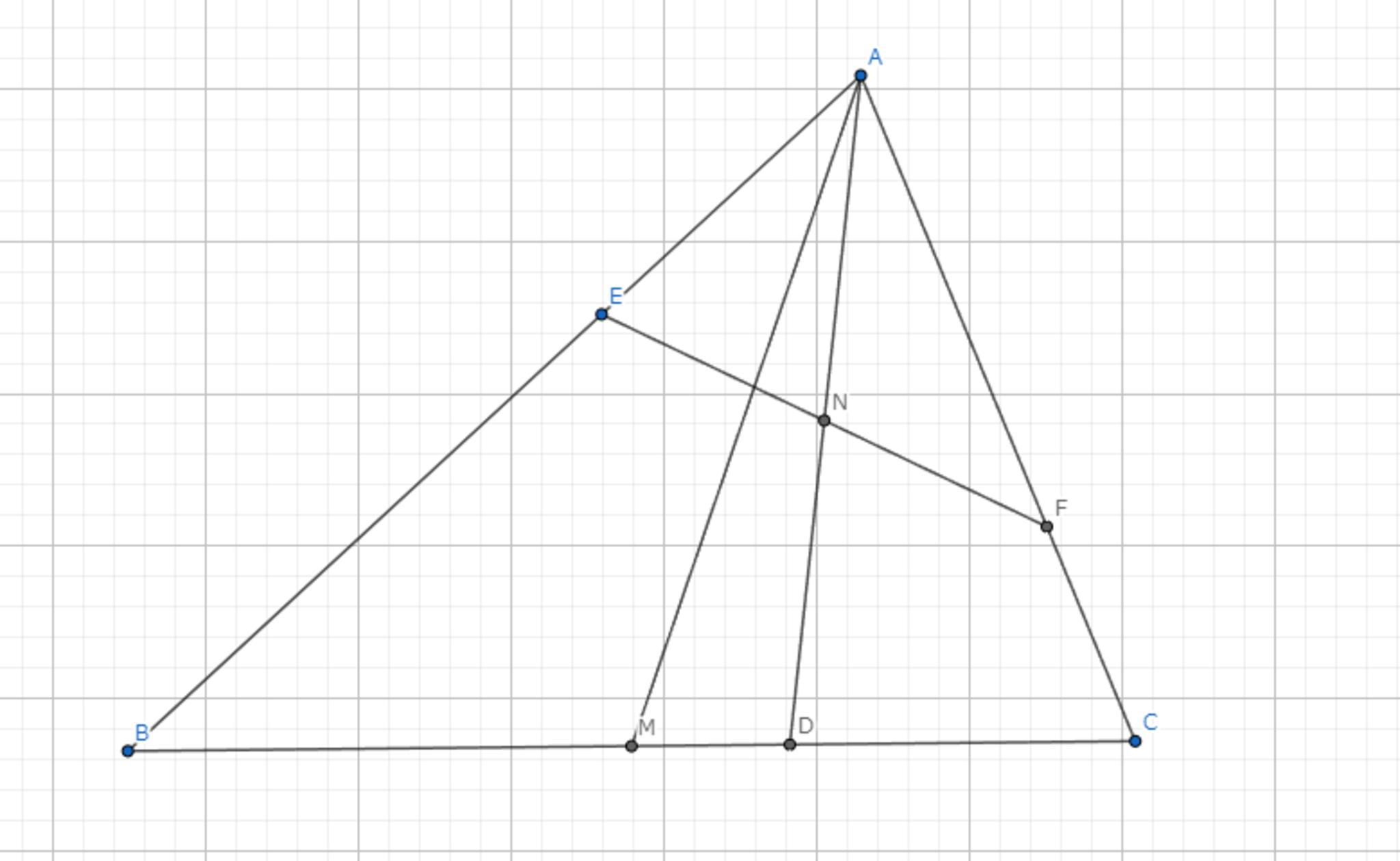
図6.定理7 -証明
ルモアーヌ点
三角形 \(ABC\) の三本のSymmedianは一点で交わる。この点をルモアーヌ点(類似重心)と呼ぶ。
証明
方針:チェバの定理の逆より \(\frac{ AF }{ FB }\cdot\frac{ BD }{ DC }\cdot\frac{ CE }{ EA }=1\) を示す。
ここで、Steiner's Ratio Theoremより \[ AF : FB = CA ^2: BC ^2 \ \ \textrm{i.e.} \ \ \frac{ AF }{ FB }=\frac{ BC ^{2}}{ CA ^{2}}\] である。 他の項に対しても同様の変形をすると、 \[\frac{ AF }{ FB }\cdot\frac{ BD }{ DC }\cdot\frac{ CE }{ EA }=\frac{ BC ^{2}}{ CA ^{2}}\cdot\frac{ CA ^{2}}{ AB ^{2}}\cdot\frac{ AB ^{2}}{ BC ^{2}}=1\] となって、3本のSymmedianは一点で交わることが示された。\(\blacksquare\)
より一般に、共点となる三線の等角共役線も共点となることが示せます。
類似重心 \(G'\) から \(BC,CA,AB\) へ下ろした垂線の長さを \(x,y,z\) とすると、\(x:y:z=BC:CA:AB\) が成り立つ。
証明
\(G'\) は3つのSymmedian上の点であるので、定理5より、\(x:y=BC:CA\)、\(y:z=CA:AB\)、\(z:x=AB:BC\) である。 よって、\(x:y:z=BC:CA:AB\) を得る。\(\blacksquare\)
三角形 \(ABC\) の内部の点 \(P\) から \(AB,BC,CA\) へ下ろした垂線の長さを \(z,x,y\) とすると、 \(x^2+y^2+z^2\) が最小となるような \(P\) は類似重心である。
証明
\(AB=c,BC=a,CA=b\) とする。 コーシーシュワルツの不等式より、\[(a^2+b^2+c^2)(x^2+y^2+z^2) \geq (ax+by+cz)^2\] が成り立つ。 \[(x^2+y^2+z^2) \geq \frac{\left(ax+by+cz\right)^{2}}{\left(a^{2}+b^{2}+c^{2}\right)} \\ \Longleftrightarrow(x^2+y^2+z^2) \geq \frac{4S^{2}}{\left(a^{2}+b^{2}+c^{2}\right)} = const \] ここでの統合成立条件は \(a:b:c=x:y:z\) でありそのような点は類似重心である。 \(\blacksquare\)
調和四角形
四角形 \(ABCD\) が円に内接して、\(AB\cdot CD=BC\cdot DA\) を満たすとき調和四角形と呼ぶ。
調和四角形は同値な言い換えがたくさん存在していて、一度経験しておかないとかなりきつい分野です。 反転なども絡めるととても美しいですが、今回は反転をメインでは扱いません。
調和四角形 \(ABCD\) において \(BD\) は三角形 \(ABC\) の B-Symmedianである。
当然、他の点に関しても同様です。
証明
\(AC, \ BD\) の交点を \(P\) とする。三角形 \(ABP,DCP\) の相似により、\(AB : DC = PA : PD = PB : PC\) を得る。 同様に、三角形 \(BCP, ADP\) の相似により、\(BC : AD = PB : PA = PC : PD\) を得る。 よって、これらを掛け合わせるなどして、 \[\frac{AB}{BC} \cdot \frac{AD}{DC} = \frac{AP}{CP}\] が得られる。また、調和四角形であったから、\(\frac{AB}{BC} = \frac{AD}{DC}\) である。 よって、 \[\left(\frac{AB}{BC}\right)^2 = \frac{AP}{CP}\] などが得られ、Steiner's ratio theorem からSymmedianであると分かる。\(\blacksquare\)
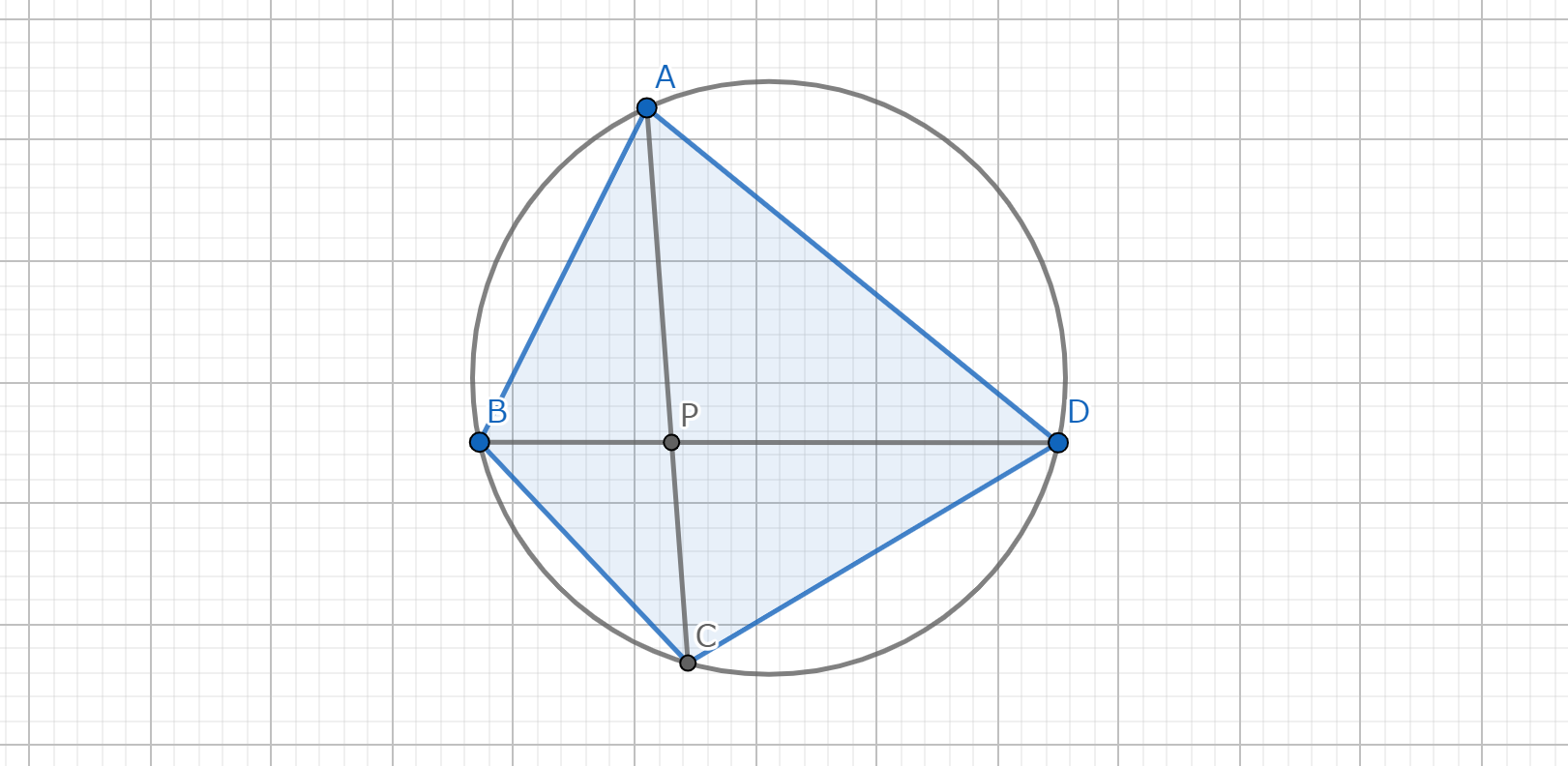
図7.定理11 -証明
名前の"調和"の由来は、調和点列です。演習問題などで少し触れますが、詳しくは複比などで触れたいですね。
演習問題
以上が基本事項です。それでは、この章が本題です。ぜひ楽しんでください!
\(\angle{A}\) を直角とする、直角三角形におけるA-Symmedianは対辺への垂線であることを示せ。
2本の接線は必ずしも一点で交わるとは限りません。そのようなケースを考えてみましょう。
証明を表示/非表示三角形 \(ABC\) において図のように \(AB, \ AC\) を一辺とする正方形を考える。 このとき、三角形 \(ADG\) の外心と \(A\) を結んだ直線はA-Symmedianとなることを示せ。
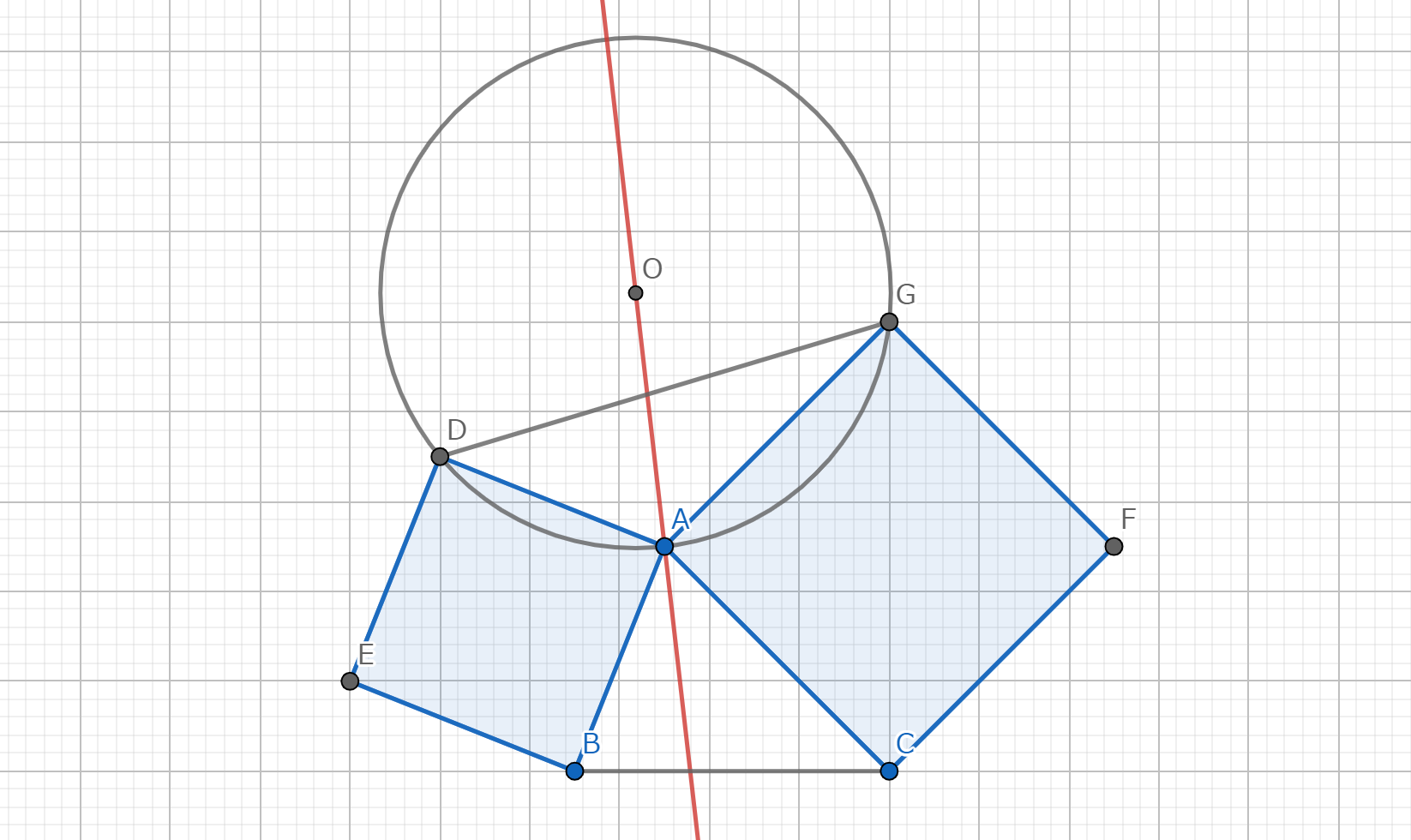
図9.問題2 -主張
これはかなり独立した(つまり、他の問題を解く上でほとんど登場しない)構図です。ただ、パズル的でおもろいです。
証明を表示/非表示三角形 \(ABC\) において、辺 \(AB,AC\) 上に \(BC//DE\) となるように点 \(D,E\) をとる。 \(BE\) と \(CD\) の交点を \(F\) とする。 三角形 \(BDF,CEF\) の外接円の交点のうち \(F\) でないものを \(G\) とするとき、\(AG\) はA-Symmedianであることを示せ。
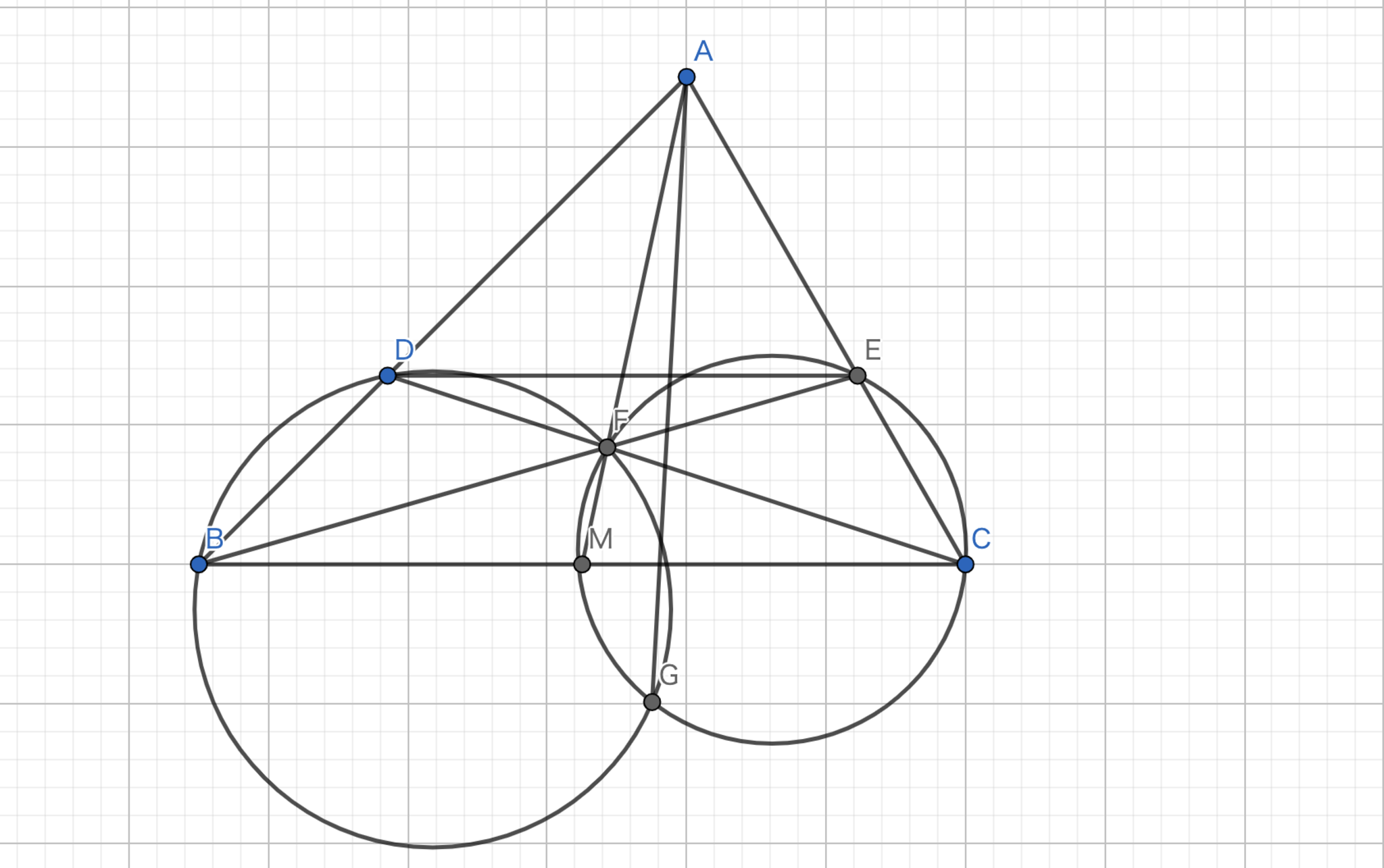
図11.問題3 -主張
これは反転でどうにかなりますが、今回は反転なしでいきます。
証明を表示/非表示三角形 \(ABC\) において、辺 \(AB,AC\) 上に \(BC//DE\) となるように点 \(D,E\) をとる。 三角形 \(BEA,CDA\) の外接円の交点のうち \(A\) でないものを \(F\) とすると、\(AF\) はA-Symmedianであることを示せ。
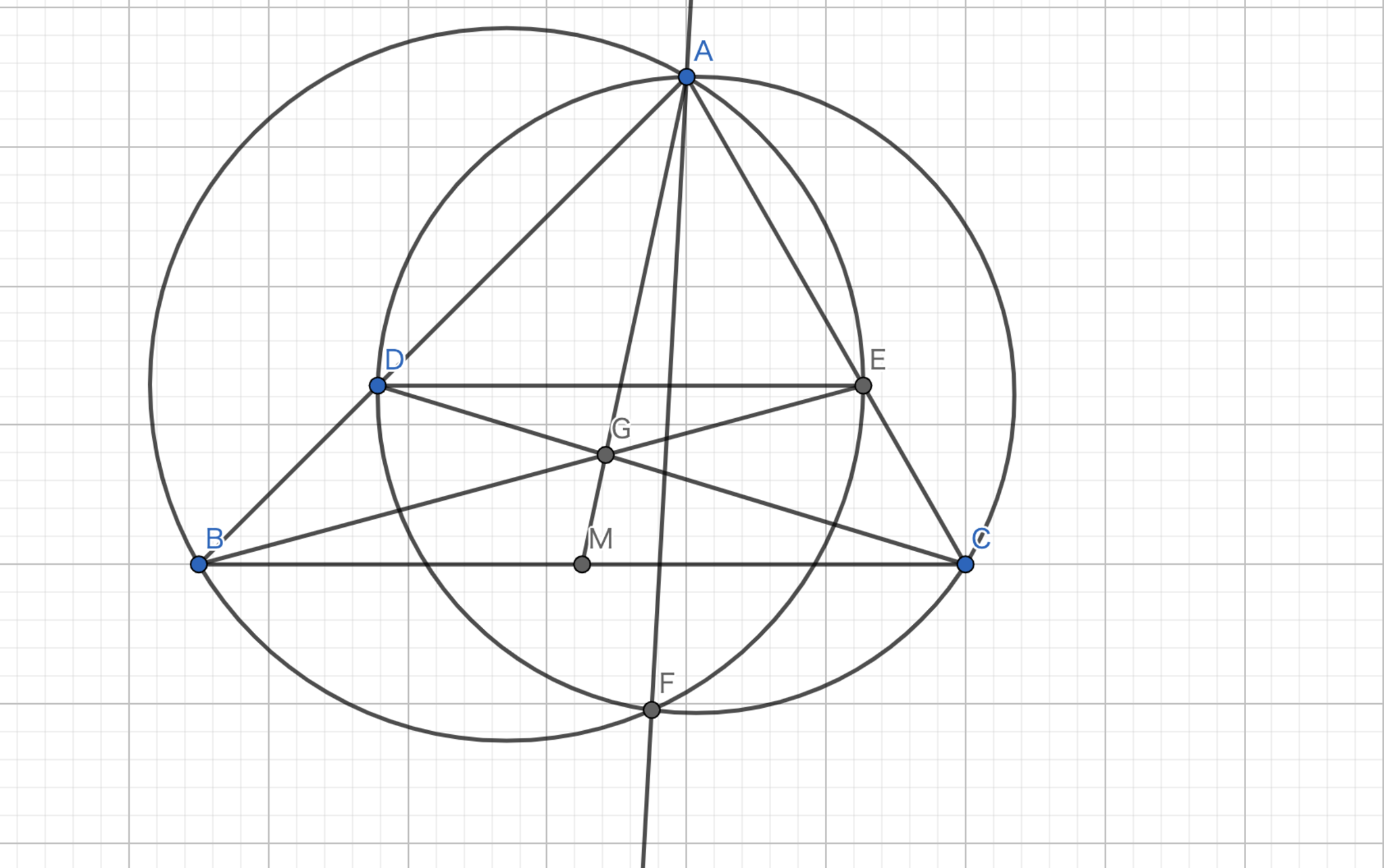
図13.問題4 -主張
これも反転でどうにかなりますが、やはり今回は反転なしでいきます。
証明を表示/非表示三角形 \(ABC\) において辺 \(AB,AC\) 上に点 \(D,E\) を \(BC//DE\) となるようにとる。 \(D\) を通り \(AC\) に逆平行な直線と \(E\) を通り \(AB\) に逆平行な直線の交点を \(F\) としたとき、\(AF\) はA-Symmedianであることを示せ。
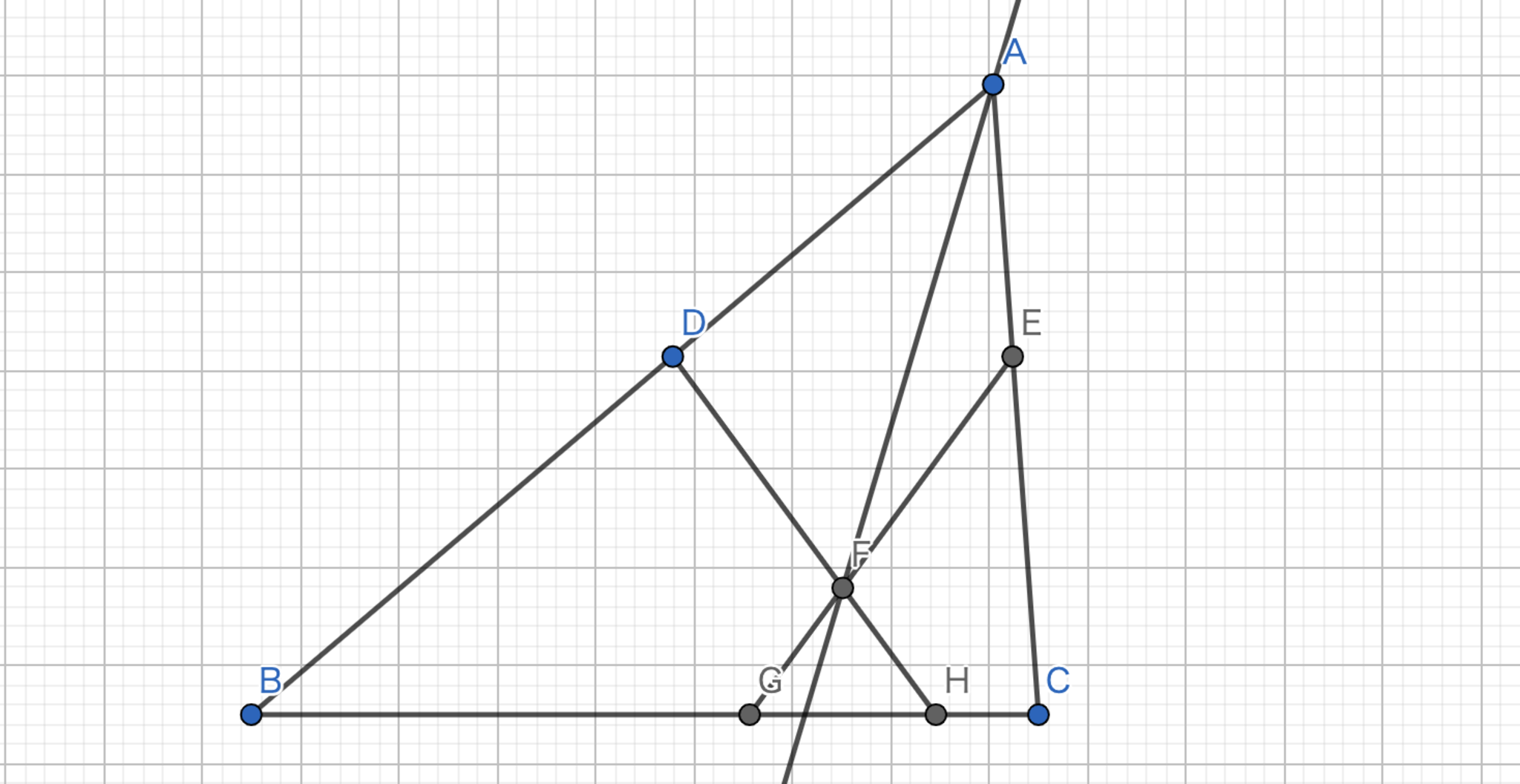
図15.問題5 -主張
円に内接する四角形 \(ABCD\) は \(AB\cdot CD=BC\cdot DA\) を満たします。 線分 \(BD\) の中点を \(M\) とします。 \(AB=127,AD=129,CM=32\) であるとき、\(AM\)の長さを求めてください。
これは4eの水diffでした。
証明を表示/非表示一直線上に点\(A,B,C \)がこの順で並んでいる。 \(AC \)を通る円のうち、中心が線分 \(AC \) 上にないものを \(\Gamma \) とする。 点 \(A,C \) における \(\Gamma \) の接線の交点を \(P \) とし、\(PB \) は \(\Gamma \) と \(Q \) で交わる。 このとき、三角形 \(AQC \) の角の二等分線と \(AC \) の交点は \(\Gamma \) の選び方に依らないことを示せ。
IMO shortlist(ISL)も簡単に解けます!
証明を表示/非表示三角形 \(ABC\) において \(B,A\) を \(A,C\) へと移す相似拡大の中心を \(X\) とする。 このとき、\(AX\) はA-Symmedianとなることを示せ。
最重要構図です!!
証明を表示/非表示この点のことを"Dumpty-point"というそうです。
三角形 \(ABC\) において、辺 \(BC\) 上に点 \(P\) をとり、\(Q,R\) を \(PQ//AB,PR//AC\) となるようにとる。 このとき、三角形 \(AQR\) の外接円は常にA-Symmedian上の一点を通ることを示せ。
AoPSはこちら。
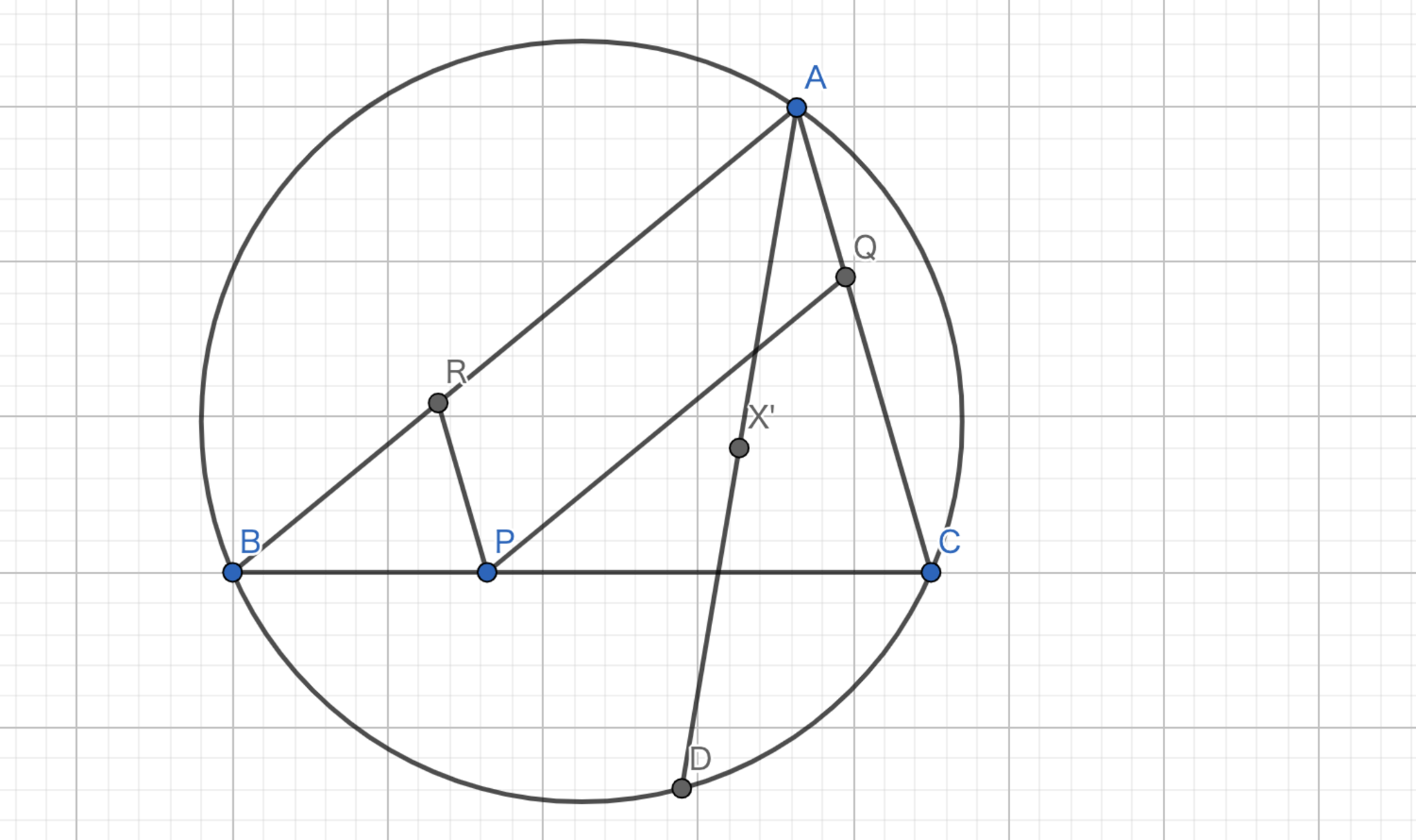
証明を表示/非表示三角形 \(ABC\) の垂心 \(H\) から中線 \(AM\) へと下ろした垂線の足を \(P\) とする。 \(P\) を \(BC\) に関して対称移動させた点を \(A'\) とすると、\(AA'\) はA-Symmedianとなることを示せ。
Symmedianの対称性に着目してみましょう.
証明を表示/非表示不等辺三角形 \(ABC\) において、その外接円を \(\Omega\) とし、\(A\) を通って \(BC\) に垂直な直線と \(\Omega\) の交点のうち \(A\) でないものを \(D\) とする。 \(B,C\) から対辺に下ろした垂線の足をそれぞれ \(E,F\) とし、三角形 \(DEF\) の外接円と \(\Omega\) の交点のうち \(D\) でない方を \(A'\) とする。 \(B',C'\) も同様に定めるときに \(AA',BB',CC'\) は一点で交わることを示せ。
引用元はこちら。
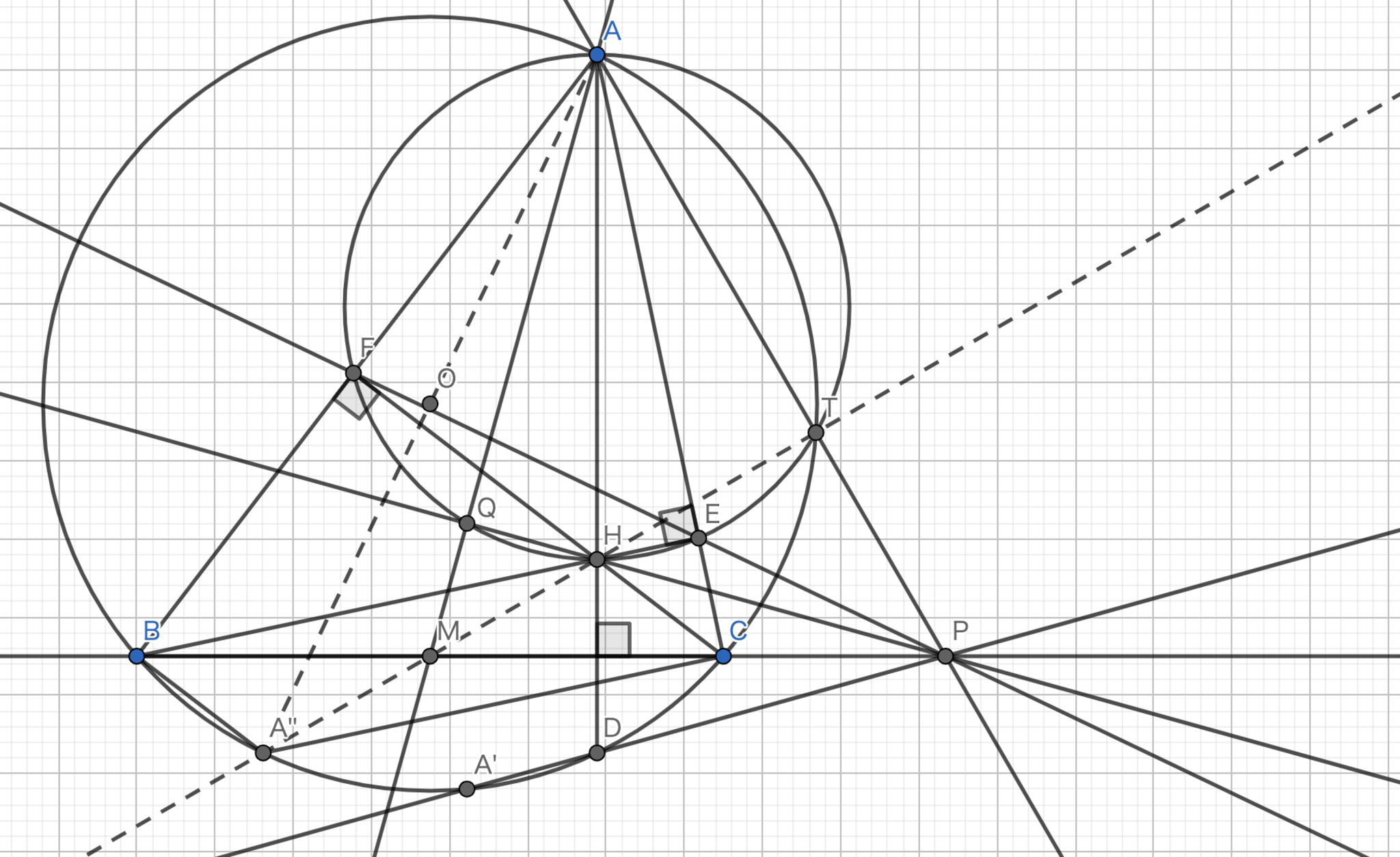
証明を表示/非表示三角形 \(ABC\) において、 \(A\) から対辺に下ろした垂線の足を \(H_A\) 、 垂心を \(H\) とし、 \(AH\) を直径とする円と三角形 \(ABC\) の外接円 \(Ω\) との交点を \(T≠A\) とする。 \(TH_A\) と \(Ω\) との交点を \(A'\) とすると、\(AA'\) はA-symmedianであることを示せ。
この構図における点 \(Q\) のことを"Humpty-point"というそうです。
三角形 \(ABC\) の外接円を \(Ω\) として、2点 \(B,C\) についてのアポロニウスの円であって \(A\) を通るようなものを \(ω\) とする。 このとき、以下の性質が成り立つ。
・\(\omega\) を \(\Omega\) で反転させても不変である。
・\(\omega\) の中心、\(A\)、 \(BC\) の中点を通る円を \(\Omega\) で反転させるとA-Symmedianとなる。
解答は省略します。ご了承ください。
参考文献
[1] What are the "humpty" and "dumpty" points?, stack exchange, https://math.stackexchange.com/questions/3894623/what-are-the-humpty-and-dumpty-points, 2024/03/07
[2] Symmedian, Brilliant, https://brilliant.org/wiki/symmedian/, 2024/03/07
[3] 中線共役線(類似中線), 新ユークリッド幾何学, http://kikagaku.at-ninja.jp/triangle_geometry/symmedian.html, 2024/03/08
[4] Steiner's Ratio Theorem, Cut The knot, https://www.cut-the-knot.org/triangle/SteinersTheorem.shtml, 2024/03/08