Feuerbach点と共線
今回は、基本的な相似拡大の問題を解いてみます。それでは、よろしくお願いします。
問題
内心を I とする三角形 ABC において、その九点円を Γ とし、頂点 B,C に対する傍接円を ωB,ωC とする。 Γ と ωB,ωC の接点をそれぞれ TB,TC とし、BTB,CTC の交点を P とする。 BI,CI と対辺の交点を UB,UC とし、TBUB,TCUC の交点を Q とする。このとき、P,Q,I が共線となることを示せ。
この解説を読むために必要な知識は、こちらの記事で解説しています。
解説
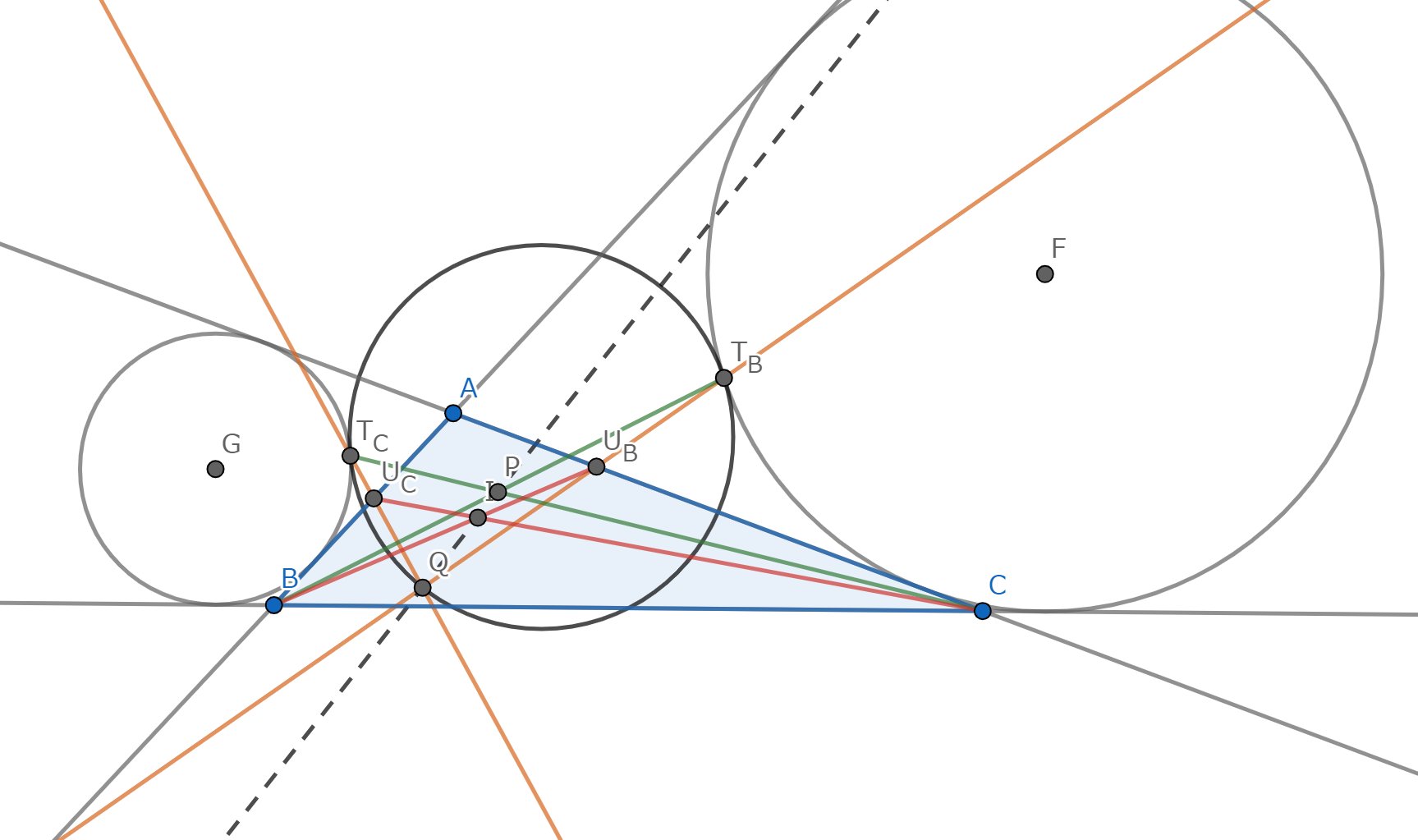
図1.問題文の図形
三角形 ABC の内接円を ω とする。ここで、以下の補題を示す。
補題1.
P は ω と Γ の内相似中心である。
証明
ω,ωB,Γ に対して、内相似中心のMongeの定理を適用することで、B,TB と ω と Γ の内相似中心が共線となることが分かる。 同様に、C,TC と ω と Γ の内相似中心も共線なので、P は ω と Γ の内相似中心である。◼
補題2.
Q はFeuerbach点である。
証明
ω,ωB,Γ に対して、補題1とは違う方法で内相似中心のMongeの定理を適用することで、UB,TB と ω と Γ の外相似中心が共線となることが分かる。 同様に、UC,TC と ω と Γ の外相似中心も共線なので、Q は ω と Γ の外相似中心、特にFeuerbach点である。◼
ω,Γ に着目すれば、それらの外相似中心、内相似中心、中心、すなわち、Q,P,I が共線であることが分かる。よって、題意は示された。◼
周辺の定理
この問題とほぼ同様にして、以下の命題を証明することができます。証明の解答はこちらです。
三角形 ABC において、その九点円を Γ とし、頂点 A,B,C に対する傍接円を ωA,ωB,ωC とする。 Γ と ωA,ωB,ωC の接点をそれぞれ FA,FB,FC とするとき、AFA,BFB,CFC は共線である。
証明は上のリンクにあります。
内心を I とする三角形 ABC において、その九点円を Γ とし、頂点 A,B,C に対する傍接円を ωA,ωB,ωC とする。 Γ と ωA,ωB,ωC の接点をそれぞれ TA,TB,TC とし、 AI,BI,CI と対辺の交点を UA,UB,UC とする。 このとき、TAUA,TBUB,TCUC は共点である。特に、その点はFeuerbach点である。
証明は上のリンクにあります。