Mongeの定理と円の相似中心
今回は、Mongeの定理(Monge d'Alembertの定理)について様々な視点から観察し、利用法を模索していきたいと思います。 この記事の本題は"拡張"以降になっています。それでは、よろしくお願いします。
前提
二つの円の中心を通る直線上には二つの相似中心が存在する。それらの二つの相似中心のうち、二円の中心を内分する位置にあるものを内相似中心と定義し、外分する位置にあるものを外相似中心と定義する。
「internal homothetic center」と「external homothetic center」の訳を意図しています。これらに対応する有名な日本語がなく、自信がなかったのでとりあえずこのサイトローカルの表記とさせていただきます。 まずは、これらの性質について確認していきましょう。
一方が他方に完全に含まないような二円 \(\omega_1,\omega_2\) において、その共通外接線の交点は外相似中心である。
証明
以下のように点を命名する。
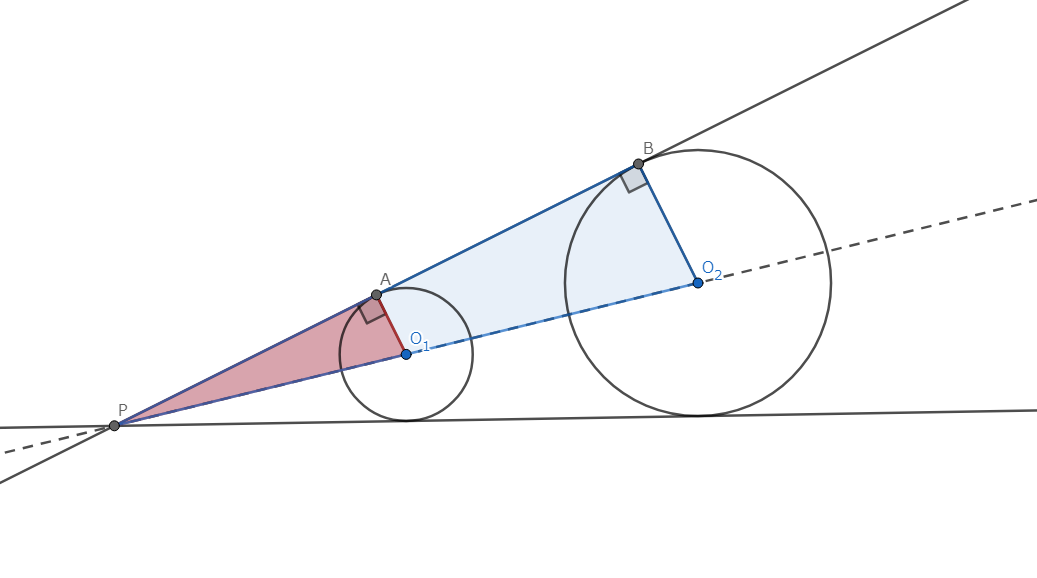
図1.共通外接線と外相似中心
\(\omega_1,\omega_2\) の外相似中心を \(P\) とし、\(\omega_1\) から \(\omega_2\) への相似変換を \(f\) とする。このとき、相似変換の倍率は 円 \(\omega_1,\omega_2\) の半径を用いて、\(\frac{R_2}{R_1}\) とする。 \(AO_1,BO_2\) は共通接線に垂直だから、\(AO_1 || BO_2\)である。また、\(f(O_1)=O_2\)、\(\frac{AO_1}{BO_2} = \frac{R_1}{R_2}\) であるから、\(f(A)=B\) である。\(\blacksquare\)
一方が他方に一部でも含まないような二円 \(\omega_1,\omega_2\) において、その共通内接線の交点は内相似中心である。
証明
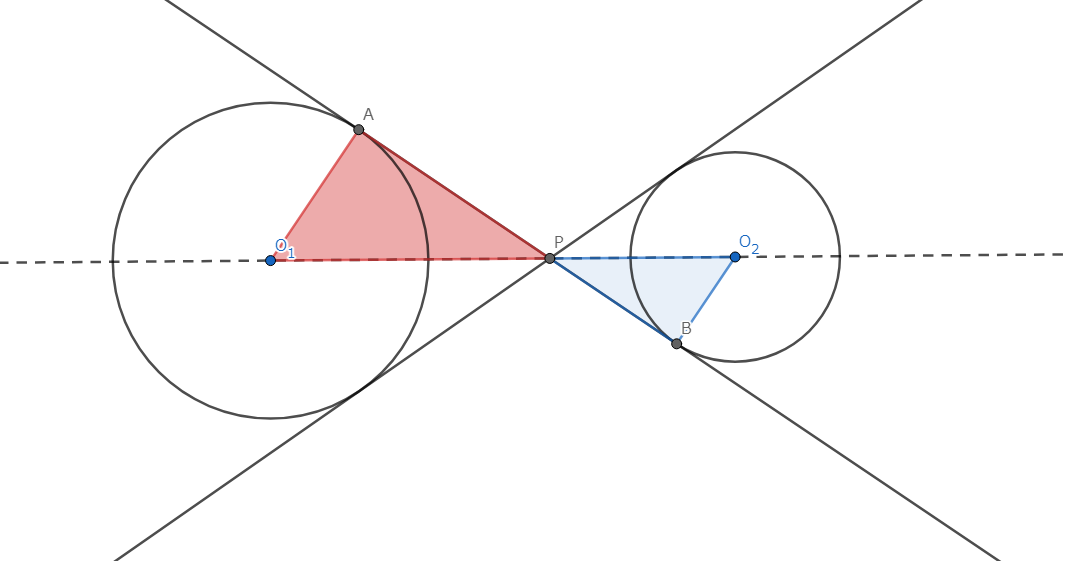
図2.共通内接線と内相似中心
定理1と全く同様にして示すことができるため略。\(\blacksquare\)
定理1,定理2において、二円が接する場合は以下のように接点が外相似中心、内相似中心となる。
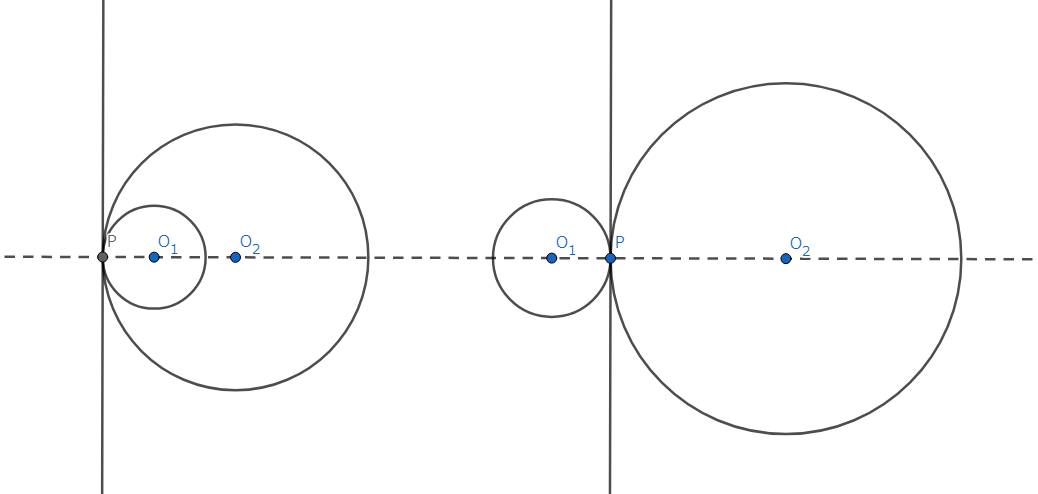
図3.二円が接する場合
これは非常によく使う状況です。また、上に述べた状況でなくても外相似中心、内相似中心は存在することに注意しましょう。 さらに、特定の条件下においては、相似中心が無限遠点に飛ぶ場合などもあることも忘れないようにしてください。
点 \(O_1,O_2\) を中心とした二円 \(\omega_1,\omega_2\) の外相似中心を \(X\) 、内相似中心を \(Y\) とするとき、四点 \(X,Y,O_1,O_2\) は調和点列となる。
証明
二円 \(\omega_1,\omega_2\) の半径を \(r_1,r_2\) とする。 \((X,Y;O_1,O_2) = \frac{XO_1}{XO_2} \cdot \frac{YO_2}{YO_1} = \frac{r_1}{r_2} \cdot \frac{r_2}{r_1} = 1\) より、題意は示された。
主張
二次元でのMongeの定理
まずは、広く知られたMongeの定理の主張を述べたいと思います。
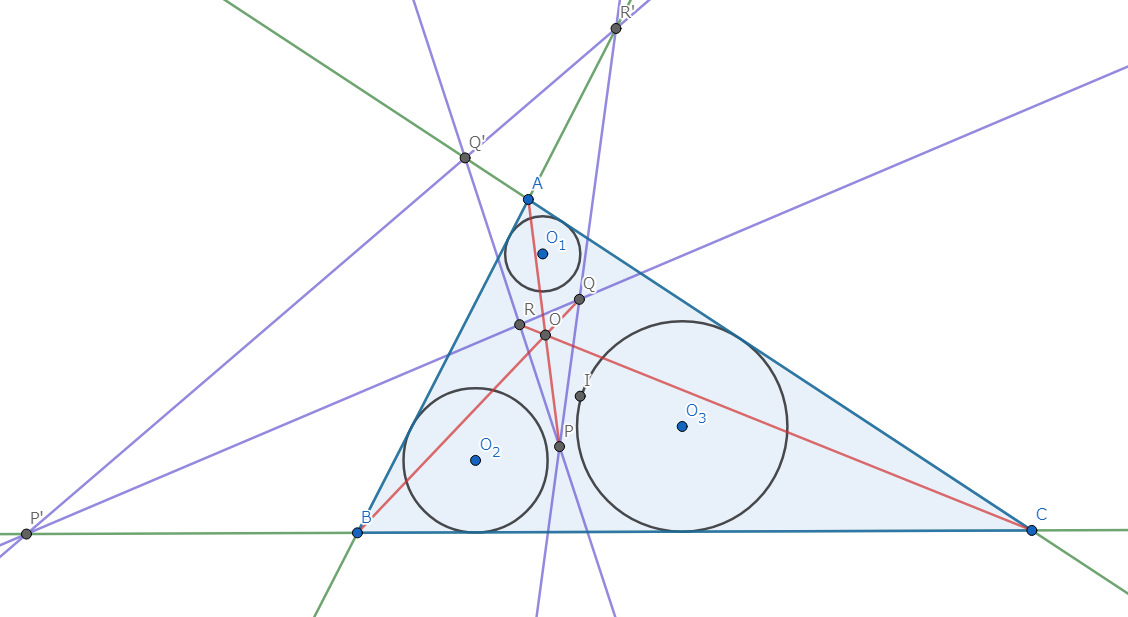
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\) の共通外接線の交点をそれぞれ \(P,Q,R\) とする。このとき、\(P,Q,R\) は共線となる。
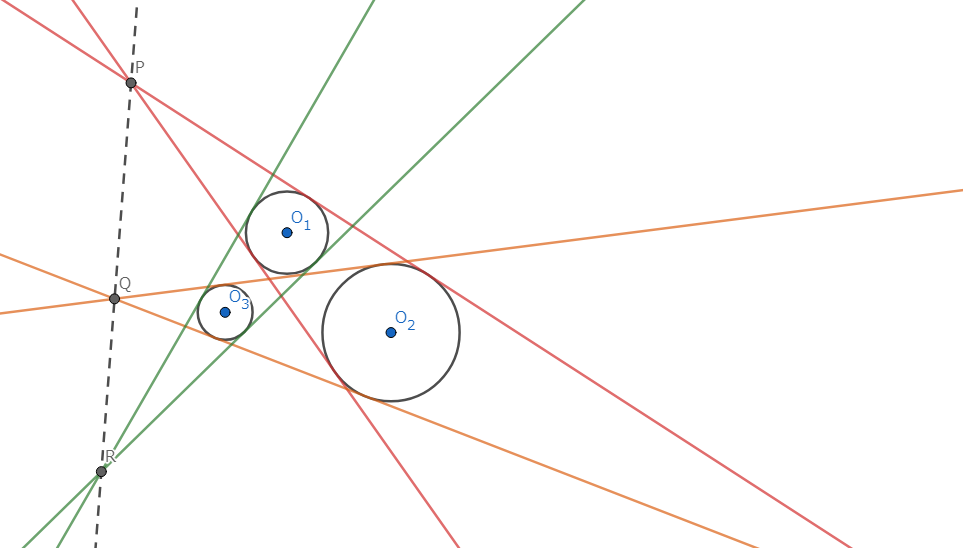
図4.Mongeの定理 (二次元)-主張
Mongeの定理は様々な視点から解釈することが可能です。その中でも、特に考察がおもしろいものは「相似拡大」と「平行射影」の二つだと思います。 そして、競技数学においても非常に強力な武器になるでしょう。 したがって、Mongeの定理には、もう少し拡張したバージョンや表現が異なるバージョンがいくつか存在しますが、それらは後でゆっくりと紹介します。次に、三次元におけるMongeの定理です。
三次元でのMongeの定理
空間内にある、互いに共有点を持たない、半径が異なった三球 \(\omega_1,\omega_2,\omega_3\) が、三球に接する平面を持つ場合、それらの共通外接線が集まる一点をそれぞれ \(P,Q,R\) とすれば、\(P,Q,R\) は共線となる。
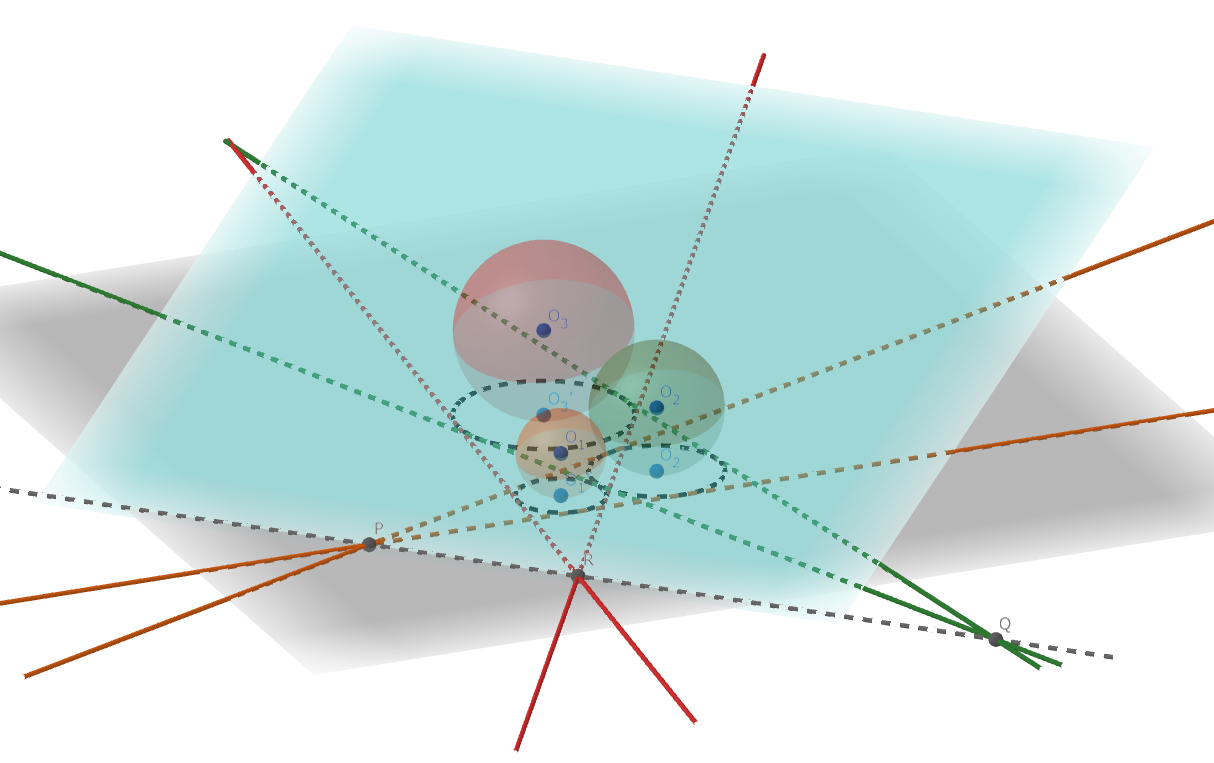
図5.Mongeの定理 (三次元)-主張
先ほど述べた通り、Mongeの定理は射影、特に平行射影という概念と深く関わっています。というのも、この三次元での定理が存在するからです。つよつよな人はこの図を見ただけで証明できてしまうかもしれませんね。
射影の詳細はこちらを参照してください。
証明 (Menelausの定理による)
まずは初等幾何による解法です。こちらは、外相似中心を自然と思いつければ余裕ですね。
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\) の共通外接線の交点をそれぞれ \(P,Q,R\) とする。このとき、\(P,Q,R\) は共線となる。
証明
三円の半径を \(r_1,r_2,r_3\) とする。 \(P,O_1,O_2\)、\(Q,O_2,O_3\)、\(R,O_3,O_1\) はそれぞれ共線である。 また、定理1より、\(P,Q,R\) は外相似中心であるから、\(\frac{O_1P}{PO_2} = \frac{r_1}{r_2}\)、\(\frac{O_2Q}{QO_3} = \frac{r_2}{r_3}\)、\(\frac{O_3R}{RO_1} = \frac{r_3}{r_1}\) を得る。 Menelausの定理の逆より、 \[\frac{O_1P}{PO_2} \cdot \frac{O_2Q}{QO_3} \cdot \frac{O_3R}{RO_1} = 1\] であるから、題意は示された。 \(\blacksquare \)
証明 (Desarguesの定理による)
Desarguesの定理に関しては、こちらをご覧ください。
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\) の共通外接線の交点をそれぞれ \(P,Q,R\) とする。このとき、\(P,Q,R\) は共線となる。
証明
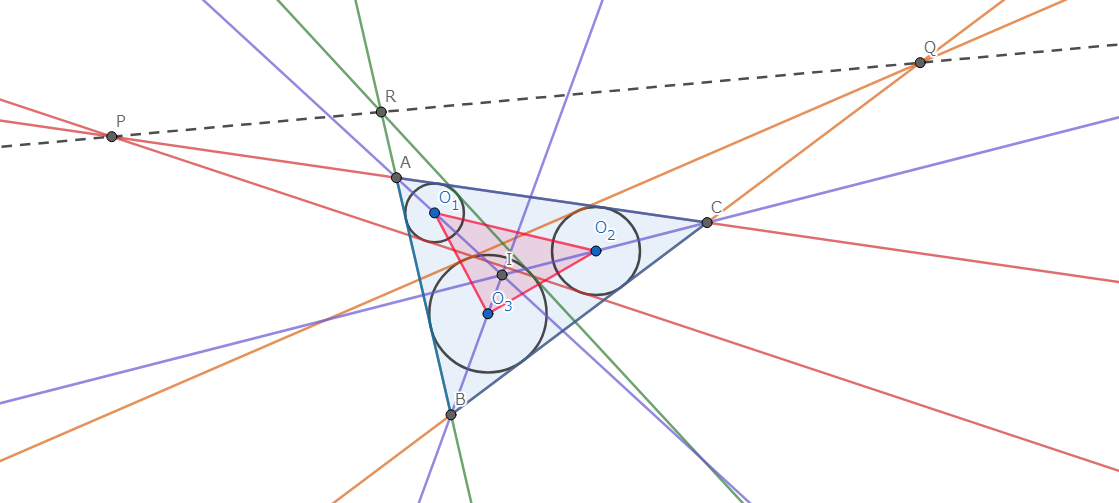
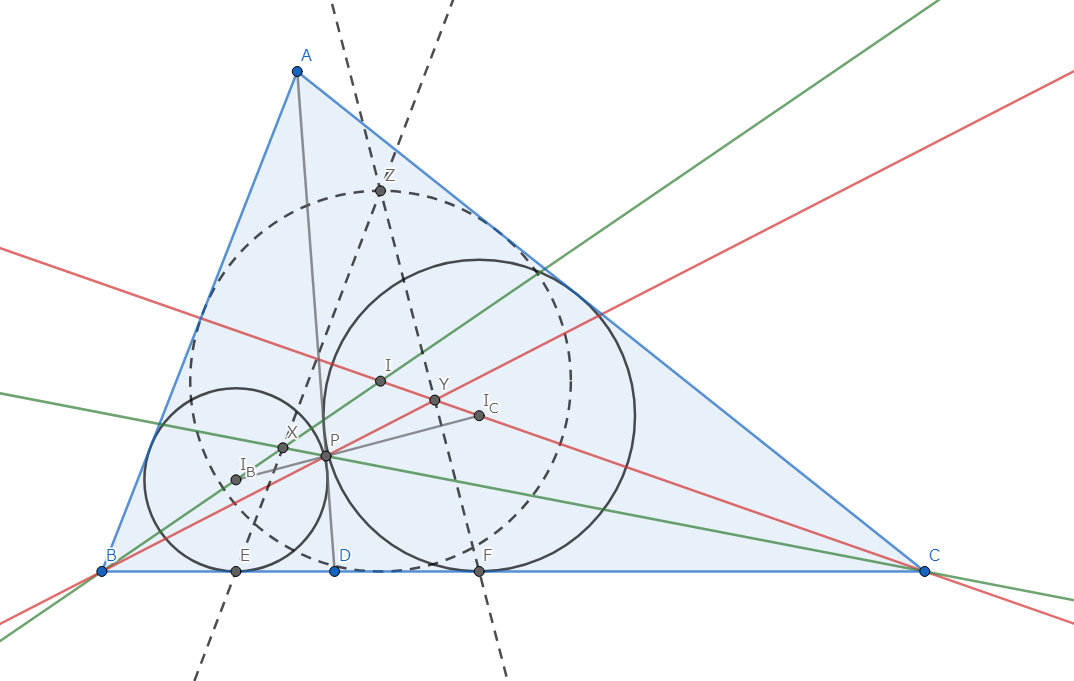
図6.Desarguesの定理によるMongeの定理の証明
図のように、\(A,B,C\) を定める。\(AO_1,BO_2,CO_3\) はその作図方法から、それぞれ \(\angle{A},\angle{B},\angle{C}\) の二等分線になっている。 よって、これらは三角形 \(ABC\) の内心 \(I\) で交わるから三角形 \(ABC,O_1O_2O_3\) に対してDesarguesの定理を適用することで \(P,Q,R\) の共線を得る。\(\blacksquare \)
証明 (平行射影による)
Mongeの定理の射影による解法です。射影についての詳しい記事はこちら。
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\) の共通外接線の交点をそれぞれ \(P,Q,R\) とする。このとき、\(P,Q,R\) は共線となる。
証明
三円が存在する平面上に接して、各円と同じ半径を持つような三球を考える。ただし、これらは三円が存在する平面に関して、同じ側にあるものとする。 このとき、後述する定理5が成り立ち、これを射影することによって目的の共線を得る。 よって、題意は示された。\(\blacksquare\)
空間内にある、互いに共有点を持たない、半径が異なった三球 \(\omega_1,\omega_2,\omega_3\) が、三球に接する平面を持つ場合、それらの共通外接線が集まる一点をそれぞれ \(P,Q,R\) とすれば、\(P,Q,R\) は共線となる。
以下の証明は、ある球が別の二つの球の間に存在しないことを仮定しています。すなわち、三球に接する平面が存在するという仮定です。 よって、平面での証明よりも限定的な場合を証明することになってしまいます。ただし、平面への射影をする場合に適切な角度で射影をすれば、平面においてはこの制約を取り除くことができます。
証明
三球が接する平面が存在するので、それらを \(P_1\) とする。 \(\omega_1,\omega_2,\omega_3\) の中心を \(O_1,O_2,O_3\) とし、その三点がなす平面を \(P_2\) とする。 三球の半径は相異なるので、\(P_1,P_2\) は平行ではなく、ある直線 \(l\) で交わる。 \(\omega_1,\omega_2,\omega_3\) と \(P_1\) の接点を \(A_{1},A_2,A_3\)とする。 このとき、\(P\) は \(A_1A_2,O_1O_2\) の交点となっているので、\(P\) は \(l\) 上に存在する。同様にして、\(Q,R\) も \(l\) 上に存在する。\(\blacksquare\)
拡張したMongeの定理
ここからが本題です。今までに紹介したMongeの定理は、「円が共有点を持たない」や「半径が相異なる」という制限がありました。 さらに、三次元の場合は平面に関する制約も追加されてしまっています。 ここからは、それらを取り除いて行きましょう。
実は、メインとなる概念は共通外接線ではありません。外相似中心と内相似中心なのです。
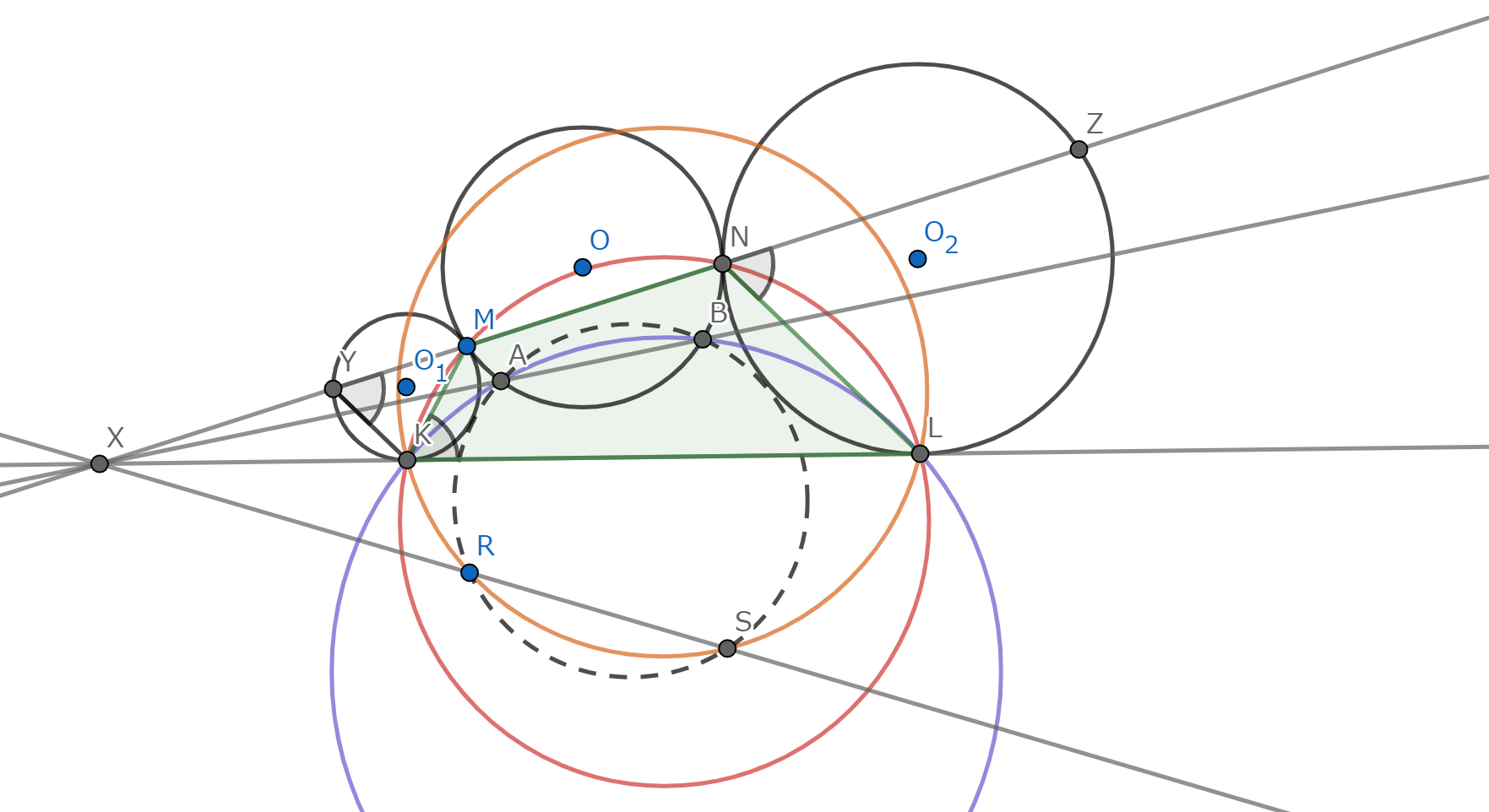
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\)に対して、以下の二つの命題が成り立つ。
\((1)\) 三つの外相似中心は共線である。
\((2)\) 一つの外相似中心と二つの内相似中心は共線である。
証明
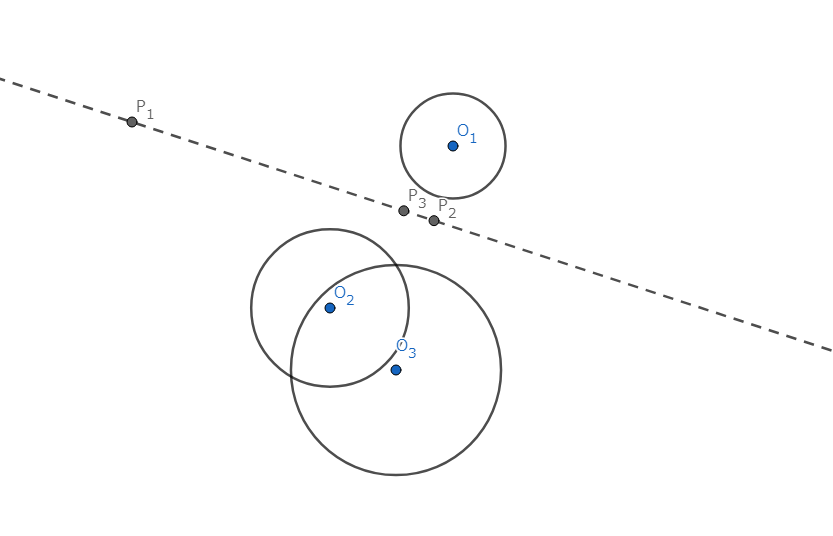
図7.Monge d'Alembertの定理 (2)
(1)
三円の中心を \(O_1,O_2,O_3\)、半径を \(r_1,r_2,r_3\)、対応する外相似中心を \(P_1,P_2,P_3\) とする。 \(P_3,O_1,O_2\)、\(P_1,O_2,O_3\)、\(P_2,O_3,O_1\) はそれぞれ共線である。 \(P_1,P_2,P_3\) は外相似中心であるから、\(\frac{O_1P_2}{P_2O_3} = \frac{r_1}{r_3}\)、\(\frac{O_3P_1}{P_1O_2} = \frac{r_3}{r_2}\)、\(\frac{O_2P_3}{P_3O_1} = \frac{r_2}{r_1}\) を得る。 Menelausの定理の逆より、 \[\frac{O_1P_2}{P_2O_3} \cdot \frac{O_3P_1}{P_1O_2} \cdot \frac{O_2P_3}{P_3O_1} = 1\] であるから、題意は示された。 \(\blacksquare \)
(2)
三円の中心を \(O_1,O_2,O_3\)、半径を \(r_1,r_2,r_3\)、対応する外相似中心を \(P_1\)、内相似中心を \(P_2,P_3\) とする。 \(P_3,O_1,O_2\)、\(P_1,O_2,O_3\)、\(P_2,O_3,O_1\) はそれぞれ共線である。 \(P_1\) は外相似中心、\(P_2,P_3\) は内相似中心であるから、\(\frac{O_1P_2}{P_2O_3} = \frac{r_1}{r_3}\)、\(\frac{O_3P_1}{P_1O_2} = \frac{r_3}{r_2}\)、\(\frac{O_2P_3}{P_3O_1} = \frac{r_2}{r_1}\) を得る。 Menelausの定理の逆より、 \[\frac{O_1P_2}{P_2O_3} \cdot \frac{O_3P_1}{P_1O_2} \cdot \frac{O_2P_3}{P_3O_1} = 1\] であるから、題意は示された。 \(\blacksquare \)
これと、定理1や定理2などを適切に組み合わせることで様々な問題を解くことができるようになります。特に、\((2)\) は頻繫に使います。
互いに共有点を持たず、半径が異なった三円 \(\omega_1,\omega_2,\omega_3\)に対して、点 \(\omega_i\) の中心と \(\omega_{i+1},\omega_{i+2}\) の内相似中心を結んだ三直線は共点である。
証明
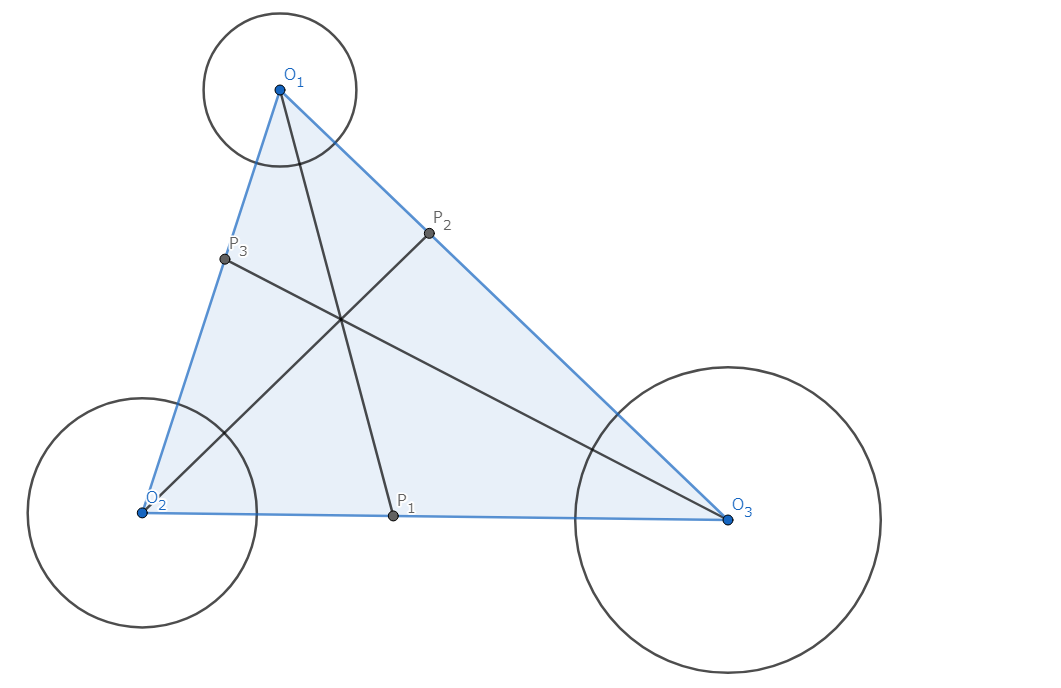
図8.内相似中心と共点
三円の中心を \(O_1,O_2,O_3\)、半径を \(r_1,r_2,r_3\)、対応する内相似中心を \(P_1,P_2,P_3\) とする。 \(P_3,O_1,O_2\)、\(P_1,O_2,O_3\)、\(P_2,O_3,O_1\) はそれぞれ共線である。 \(P_1,P_2,P_3\) は内相似中心であるから、\(\frac{O_1P_2}{P_2O_3} = \frac{r_1}{r_3}\)、\(\frac{O_3P_1}{P_1O_2} = \frac{r_3}{r_2}\)、\(\frac{O_2P_3}{P_3O_1} = \frac{r_2}{r_1}\) を得る。 Cevaの定理の逆より、 \[\frac{O_1P_2}{P_2O_3} \cdot \frac{O_3P_1}{P_1O_2} \cdot \frac{O_2P_3}{P_3O_1} = 1\] であるから、題意は示された。 \(\blacksquare \)
いつ使うべきか?
Mongeの定理、Monge d'Alembertの定理の真価は複数の円が接しているときに発揮されます。 そのような状況で、反転で倒せない問題だったら、まずはこれらの定理を含めた相似拡大がテーマの問題であることを疑ってみると良いかもしれません。 その他には、単純に相似拡大が絡む場合は良く出てきます。相似から角度の情報が得られることも良くあります。
演習問題
Monge d'Alembertの定理と二円の相似に関する問題を扱っていきます。
三角形 \(ABC\) の外接円を \(\Gamma\) とする。辺 \(AB,AC\) に接し、\(\Gamma\) に内接する円を \(\Gamma_A\)、辺 \(BC,BA\) に接し、\(\Gamma\) に内接する円を \(\Gamma_B\)、辺 \(CA,CB\) に接し、\(\Gamma\) に内接する円を \(\Gamma_C\) とする。 円 \(\Gamma\) と \(\Gamma_A,\Gamma_B,\Gamma_C\) との接点をそれぞれ \(P,Q,R\) とおく。直線 \(AP,BQ,CR\) は一点で交わることを示せ。
頂点と、混線内接円(mixtilinear incircle)と外接円の接点を結んだときに、共点となる事を示せという問題ですね。本選3番級にしてはかなり簡単だと思います。 相似中心の概念を知っていれば瞬殺ですし、知らなくても反転や等角共役点の知識で解くことができます。
証明を表示/非表示三角形 \(ABC\) の \(A,B,C\) に関する傍接円をそれぞれ \(\Gamma_A,\Gamma_B,\Gamma_C\) とし、九点円を \(\Gamma\) とする。 \(\Gamma_A,\Gamma_B,\Gamma_C\) と \(\Gamma\) の接点をそれぞれ \(F_A,F_B,F_C\) とするとき、\(AF_A,BF_B,CF_C\) が共点となる事を示せ。
各頂点と傍接円に関するFeuerbach点を結んだときに、共点となる事を示せという問題ですね。これも一撃です。もちろん、Feuerbachの定理を証明する必要はありません。
証明を表示/非表示内心を \(I\) とする三角形 \(ABC\) の \(A,B,C\) に関する傍接円をそれぞれ \(\Gamma_A,\Gamma_B,\Gamma_C\) とし、九点円を \(\Gamma\) とする。 \(AI,BI,CI\) と各辺の交点をそれぞれ \(P,Q,R\) とする。 \(\Gamma_A,\Gamma_B,\Gamma_C\) と \(\Gamma\) の接点をそれぞれ \(F_A,F_B,F_C\) とするとき、\(PF_A,QF_B,RF_C\) が共点となる事を示せ。
こちらは問題2-1とほぼ同様です。
証明を表示/非表示三角形 \(ABC\) において、\(\omega_A,\omega_B,\omega_C\) をそれぞれ、\(AB,AC\) 、\(BC,BA\)、 \(CA,CB\) に接する円とする。 \(P,Q,R\) を \(\omega_B,\omega_C\) 、\(\omega_C,\omega_A\) 、\(\omega_A,\omega_B\) の内相似中心とするとき、\(AP,BQ,CR\) が共点であることを示せ。
難易度的には、Easy Little Mathematical Olympiad (簡単よわよわ数学オリンピック)ですね。
証明を表示/非表示直線 \(l\) の同じ側に三円 \(\omega_1,\omega_2,\Omega\) が存在し、\(\omega_1,\omega_2\) は直線 \(l\) と点 \(K,L\) でそれぞれ接し、\(\Omega\) と点 \(M,N\) でそれぞれ接している。 また、\(\omega_1,\omega_2\) は交わらず、異なる半径を持つ。 \(K,L\) を通る円 \(\Gamma\) が \(\Omega\) と 点 \(A,B\) で交差している。 直線 \(l\) に関して、\(M,N\) を対称移動させた点を \(R,S\) とするとき、四点 \(A,B,R,S\) が共円となる事を示せ。
これは良問だと思います。かなり好きです。相似中心は、当たり前ですが、相似の中心です。
証明を表示/非表示内心を \(I\) とする三角形 \(ABC\) において、辺 \(BC\) 上に点 \(D\) をとり、\(\omega_B,\omega_c\) を三角形 \(ABD,ACD\) の内接円とする。 三角形 \(\omega_B,\omega_C\) の中心を \(I_B,I_C\) とし、辺 \(BC\) の接点をそれぞれ \(E,F\) とする。 \(I_BI_C,AD\) の交点を \(P\) とし、\(BI,CP\) の交点を \(X\) とし、\(CI,BP\) の交点を \(Y\) とする。 このとき、\(EX,FY\) の交点が三角形 \(ABC\) の内接円上で交わることを示せ。
これはTSTST 5番級にしては易しいと思います。
証明を表示/非表示三つの円弧 \(\gamma_1,\gamma_2,\gamma_3\) が点 \(A,C\) を共有している。 これらの円弧は直線 \(AC\) に対して同じ側にあり、\(\gamma_2\) は \(\gamma_1,\gamma_3\) の間にある。 点 \(B\) は線分 \(AC\) 上にある。 点 \(B\) を始点とする半直線 \(h_1,h_2,h_3\) は直線 \(AC\) に対して円弧と同じ側にあり、\(h_2\) は \(h_1,h_3\) の間にある。 \(i,j=1,2,3\) に対して、点 \(V_{ij}\) を \(h_i\) と \(\gamma_j\) の交点とする。(以下の図を参照せよ。)
"湾曲四角形":\(\widehat{V_{ij}V_{kj}} \ \widehat{V_{kl}{V_{il}}}\) を弧 \(\widehat{V_{ij}V_{kj}}\)、\(\widehat{V_{kl}{V_{il}}}\)、直線 \(V_{ij}V_{il}\)、\(V_{kj}V_{kl}\) で囲まれる図形と定義する。 この"湾曲四角形"が円に外接しているとは、二直線と二円弧全てに接するような円が存在することを指す。 \(\widehat{V_{11}V_{21}} \ \widehat{V_{22}{V_{21}}}\)、\(\widehat{V_{12}V_{22}} \ \widehat{V_{23}{V_{13}}}\)、\(\widehat{V_{21}V_{31}} \ \widehat{V_{32}{V_{22}}}\) が円に外接しているならば、\(\widehat{V_{22}V_{32}} \ \widehat{V_{33}{V_{23}}}\) が円に外接していることを示せ。
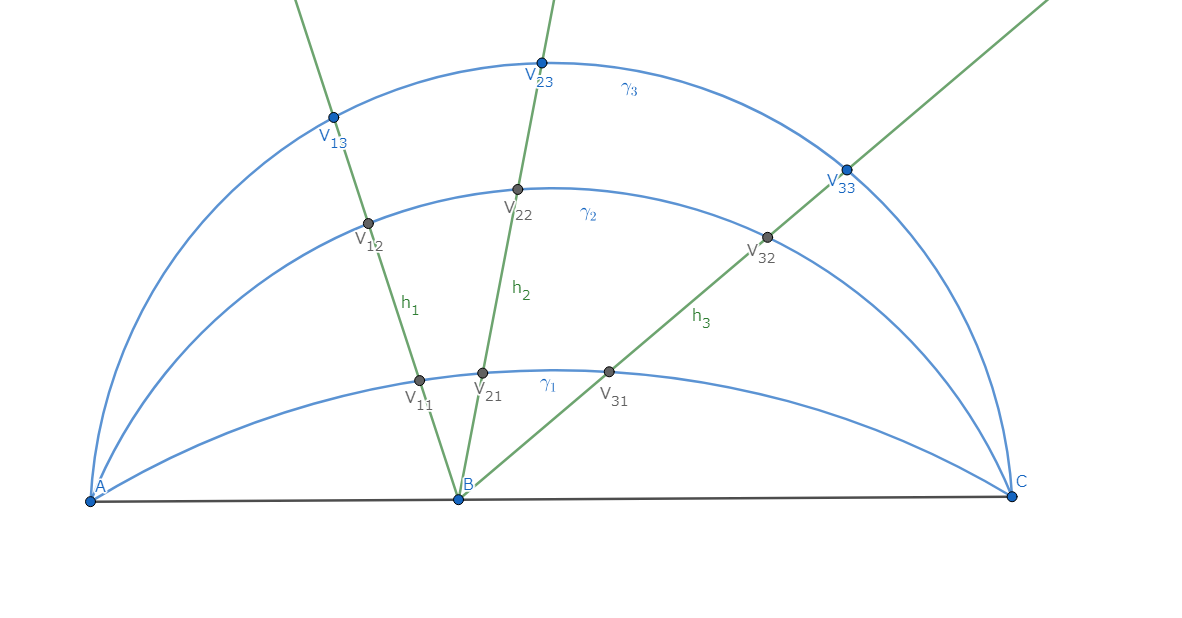
見た目はキモイですが、やることはそこまで複雑ではありません。
証明を表示/非表示参考文献
[1] 西山 享, 射影幾何学の考え方(数学のかんどころ 19)
[2] Dr. Suzy Manuela Prajea, Concurrency, Coliniarity, and Cyclicity using Homotheties