幾何学における平行射影
今回は、射影幾何学の入門として平行射影と点射影について扱っていきたいと思います。それでは、よろしくお願いします。
平行射影
射影(平行射影)とは?
三次元空間 \(\mathbb{R}^3\) において、平行射影を以下のように定義する。
射影したい点 \(P(x,y,z)\) 、方向ベクトル \(\boldsymbol{v} = (a,b,c)\)、射影先の平面を \(\mathbb{X}\) とする。ただし、\(\boldsymbol{v}\) と \(\mathbb{X}\) の法線ベクトルは垂直でない。 以下の条件を満たす \(t\) がただ一つ存在するので、射影先 \(Q\) は \(P + t\boldsymbol{v}\) で与えられる:
- 点 \(P + t\boldsymbol{v}\) が \(\mathbb{X}\) 上にある。
このようにして、点から平面への写像 \(f_{\boldsymbol{v}}: P \in \mathbb{R}^3 \to Q \in \mathbb{X}\) を構築し、これを平行射影という。
(\(\mathbb{X}\) という文字を使ったのは、最近Twitterが \(\mathbb{X}\) に変わったからです。それだけです。)
平行射影とは、空間内の物体にある角度から光を当てて面に影を作ることを指します。これはアート、工学、建築などの分野でよく使用される概念で、特に3次元空間におけるオブジェクトの2次元への投影に利用されます。
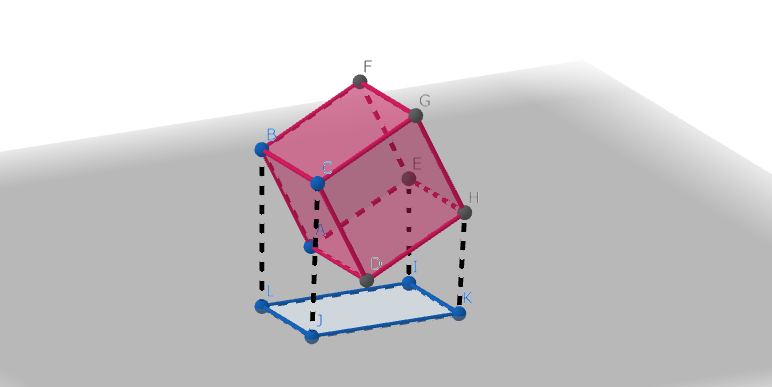
図1.直方体のある平面への正射影
特に、射影先の面に対して垂直な射影を行う場合に正射影と呼びます。 もちろん、平行射影は点単体に適用するよりも、図形に適用することで真価を発揮します。 以下は平行射影によって移る図形の一覧です。是非とも、ご自身でも確認してみてください。
- 点 → 点
- 直線 → 直線
- 多角形 → 多角形
- 楕円 → 楕円
- 放物線 → 放物線
- 双曲線 → 双曲線
- 球 → 円
- 多面体 → 多角形
さらに、図形だけでなく、図形の性質も一部移り変わります。
- 交点 → 交点
- 接点 → 接点
- 平行 → 平行
平行射影の便利な性質
ここでは、いくらか平行射影の便利な性質を紹介していきます。証明に関しては、計算を行うだけなので省略します。
平行四辺形 \(ABCD\) があり、任意の平行四辺形 \(A'B'C'D\) に対してある平行射影が存在し、\(ABCD\) が \(A'B'C'D'\) に移る。
証明
略
円 \(\Gamma\) があり、任意の二次曲線 \(\Gamma'\) に対してある平行射影が存在し、\(\Gamma\) が \(\Gamma'\) に移る。
証明
略
応用例
この平行射影という概念は「それはそう。」と言った感じでいまいち使いどころが分からないかもしれません。 しかし、この平行射影を使うことでいくらかの幾何学の定理が自明に証明できてしまいます。
1.Desarguesの定理
二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
平行射影の基本的な利用法です。Desarguesの定理の二次元における証明はそこそこ難しいです。対して、三次元のDesarguesの定理は二平面の交わりが直線であることさえ分かれば理解できてしまうほどにシンプルです。 証明の詳細はこちらを参照してください。
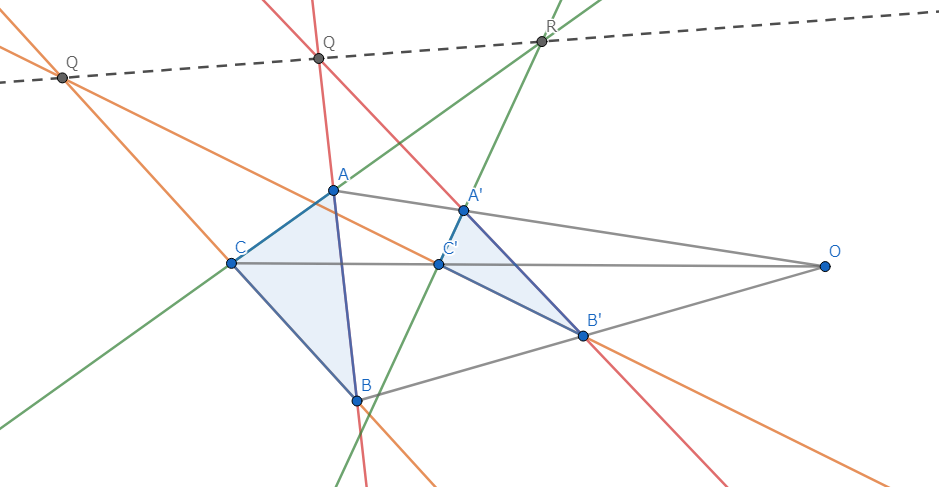
図2.Desarguesの定理 (二次元)
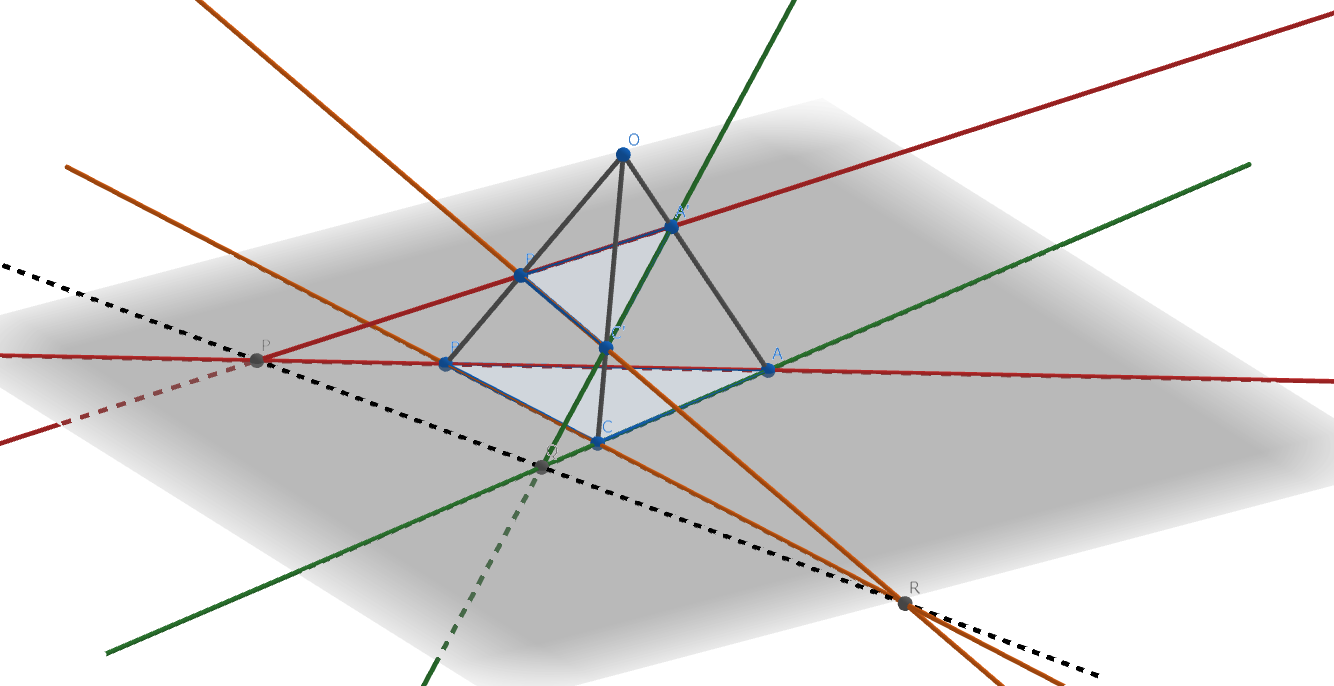
図3.Desarguesの定理 (三次元)
2.Mongeの定理
\(O_1,O_2,O_3\) を中心とする円 \(\Gamma_1,\Gamma_2,\Gamma_3\) が存在し、\(\Gamma_1,\Gamma_2,\Gamma_3\) において、それらの共通外接線の交点は共線である。
こちらも平行射影の基本的な利用法です。Mongeの定理の二次元における証明もひと手間あります。 こちらもDesarguesの定理同様、二平面の交わりが直線であることさえ分かれば理解できてしまうほどにシンプルです。 証明の詳細はこちらを参照してください。
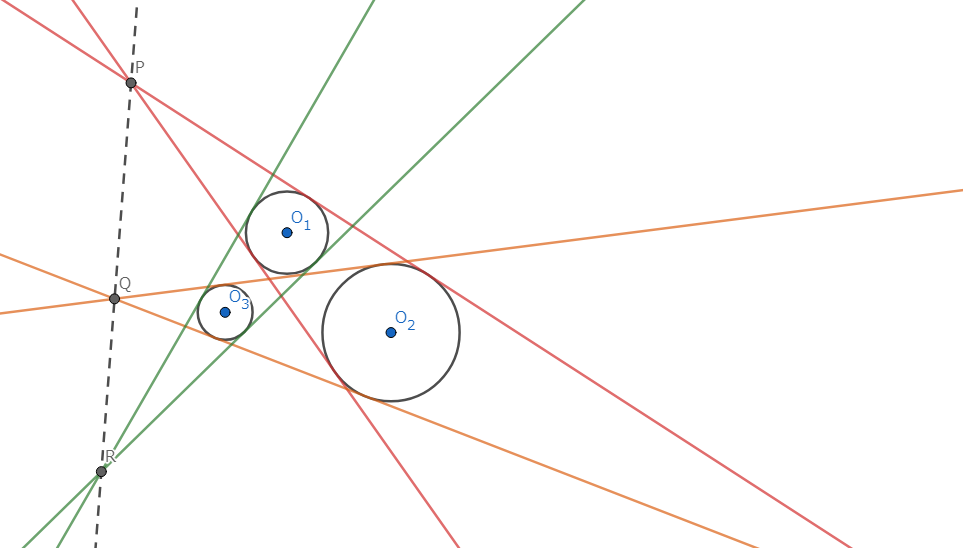
図4.Mongeの定理 (二次元)
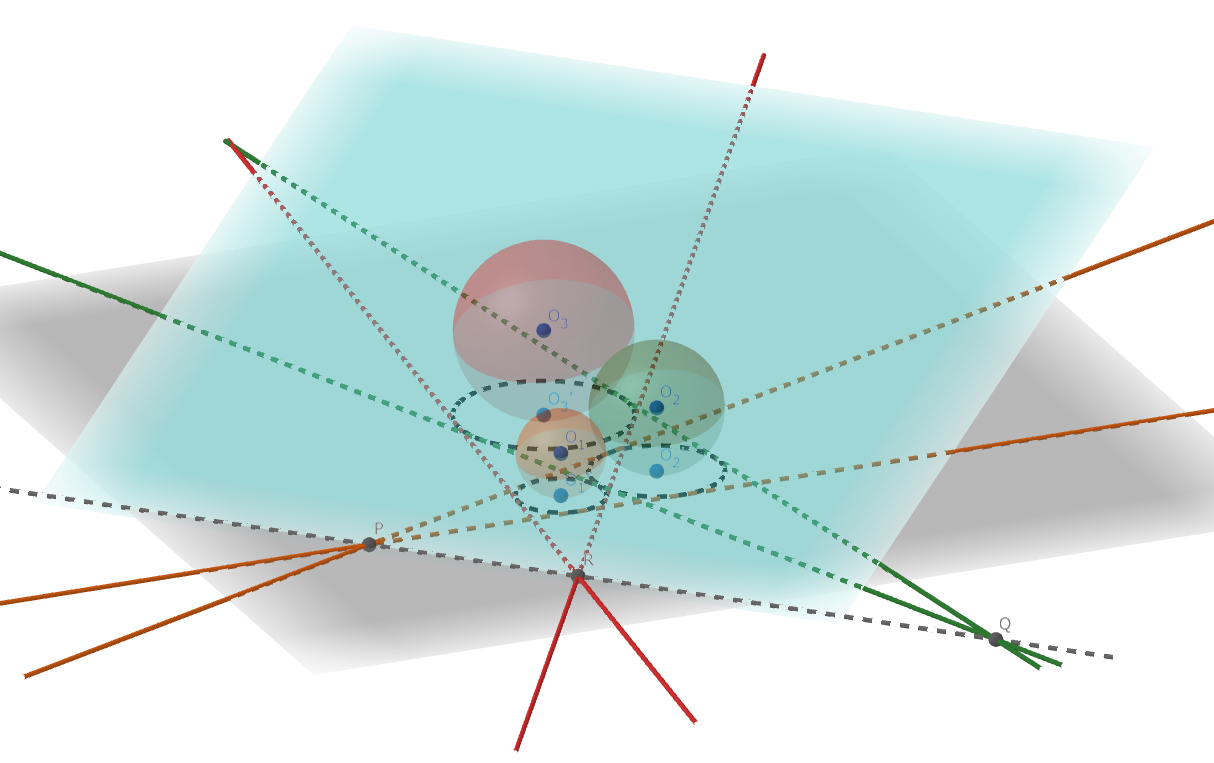
図5.Mongeの定理 (三次元)
3.根心の存在定理
\(O_1,O_2,O_3\) を中心とする円 \(\Gamma_1,\Gamma_2,\Gamma_3\) において、それらの根軸は共点である。
ちょっとマニアックかもしれませんが、とても面白いです。 こちらは、空間内部の三球が一点以上で交わることが分かれば十分です。 証明の詳細はこちらを参照してください。
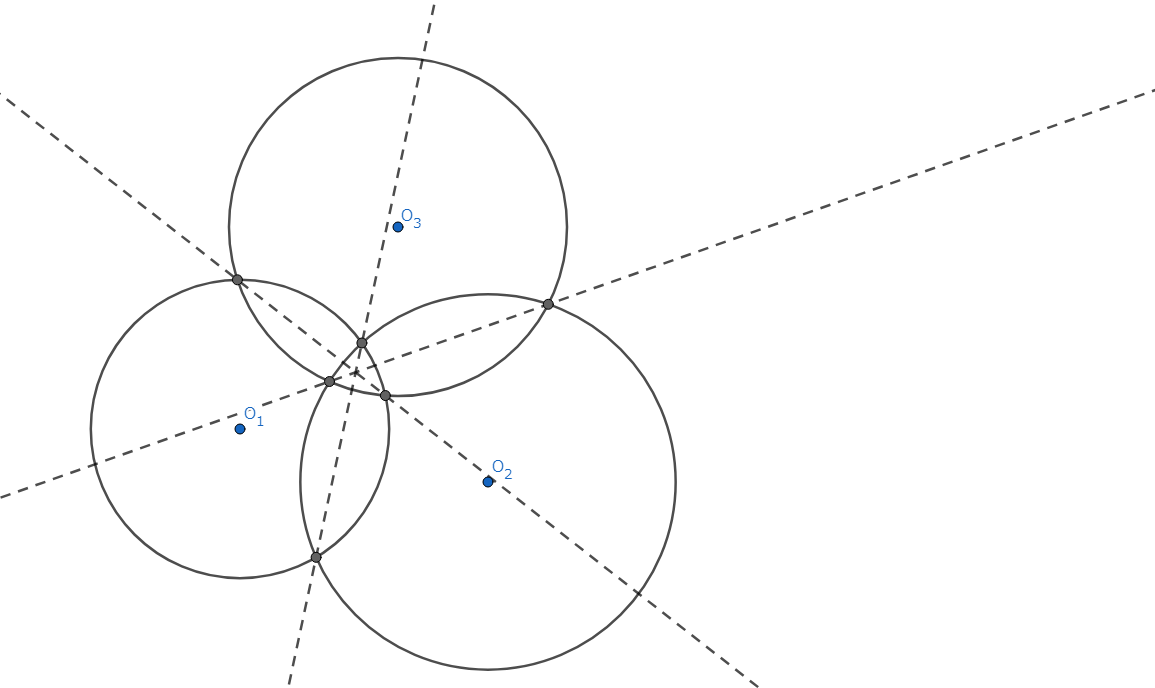
図6.根心の存在定理 (二次元)
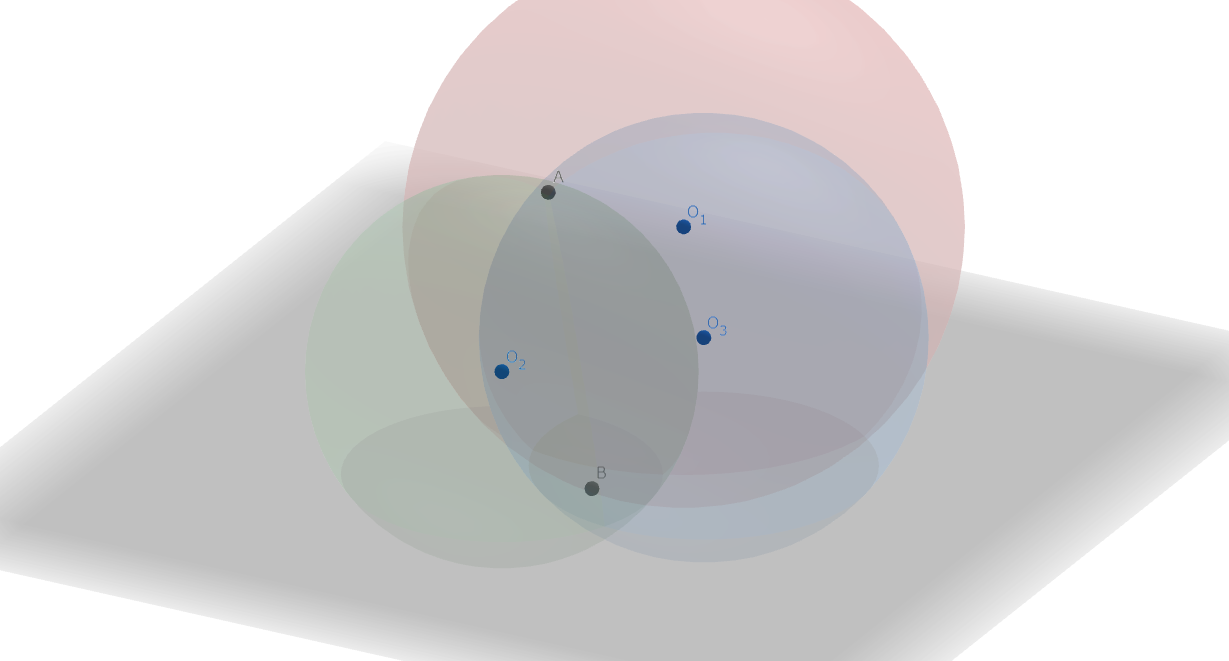
図7.根心の存在定理 (三次元)
4.Gergonneの定理
上の1,2,3の例は初等幾何学の定理を射影を用いて楽に証明することができる点にその利点がありました。 4では視点を変えて、ある定理を拡張する効果を見ていきます。
まずは、通常のGergonneの定理を紹介します。
三角形 \(ABC\) において、内接円と各辺の接点を \(P,Q,R\) とするとき、\(AP,BQ,CR\) は共点である。
証明
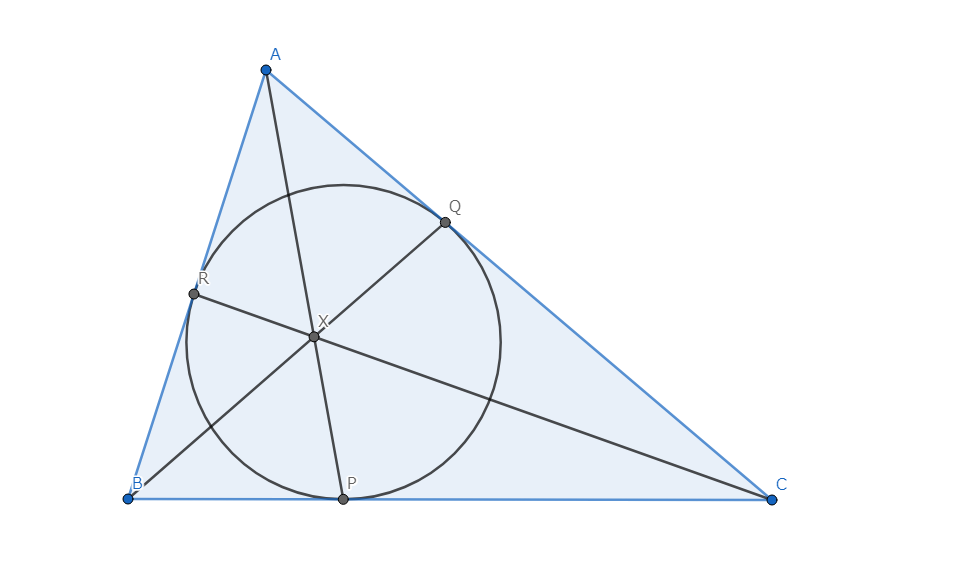
図7.Gergonneの定理
円外からの二接線の距離は等しいから、\(AQ=AR,BR=BP,CP=CQ\) である。チェバの定理より、 \[\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} = 1\] であるから共点である。\(\blacksquare\)
三角形 \(ABC\) において、内接楕円と各辺の接点を \(P,Q,R\) とするとき、\(AP,BQ,CR\) は共点である。
証明
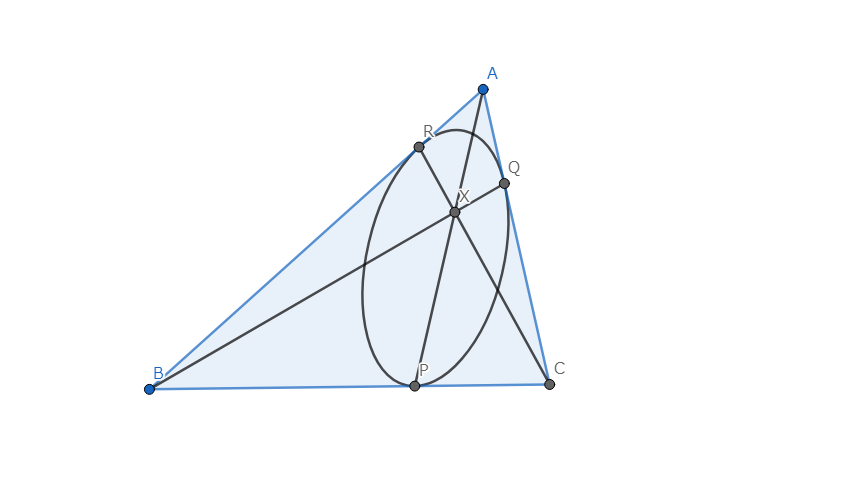
図9.Gergonneの定理 (拡張)
楕円は、ある平行射影が存在して円へと移り変わるから拡張されていないGergonneの定理へと帰着することができる。よって、題意は示された。\(\blacksquare\)
5.その他いろいろ
Gergonneの定理のように、射影幾何的な定理では(例外はあれども)多くの場合で二次曲線へと拡張することができます。 ある命題の円での成立が証明できたら、二次曲線での平行射影によって拡張できないかを考えてみるのは良いと思います。 以下に、二次曲線への拡張が可能な定理の一部を列挙してみます。
- Pascalの定理
- Brianchonの定理
- 胡蝶定理
参考文献
[1] 西山 享, 射影幾何学の考え方(数学のかんどころ 19)