Desarguesの定理と自己双対
今回は、Desarguesの定理について様々な視点から観察し、利用法を模索していきたいと思います。それでは、よろしくお願いします。
主張
二次元でのDesarguesの定理
二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
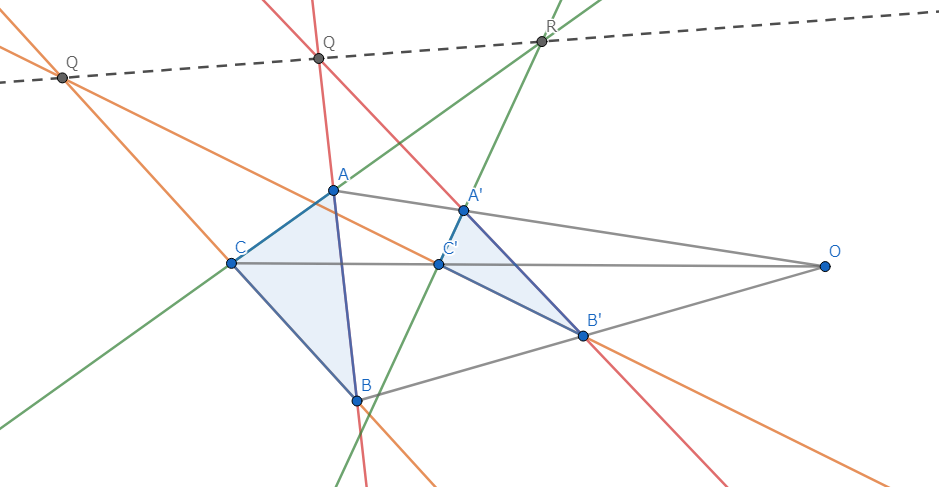
図1.Desarguesの定理 (二次元)-主張
Desarguesの定理は本当に神です。 数学的にも重要なのですが、絵画やCGなどにの祖となっています。 この定理を導入することで、様々な初等幾何学の定理が自明なものになってとてもありがたいのです。
三次元でのDesarguesの定理
空間内の二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
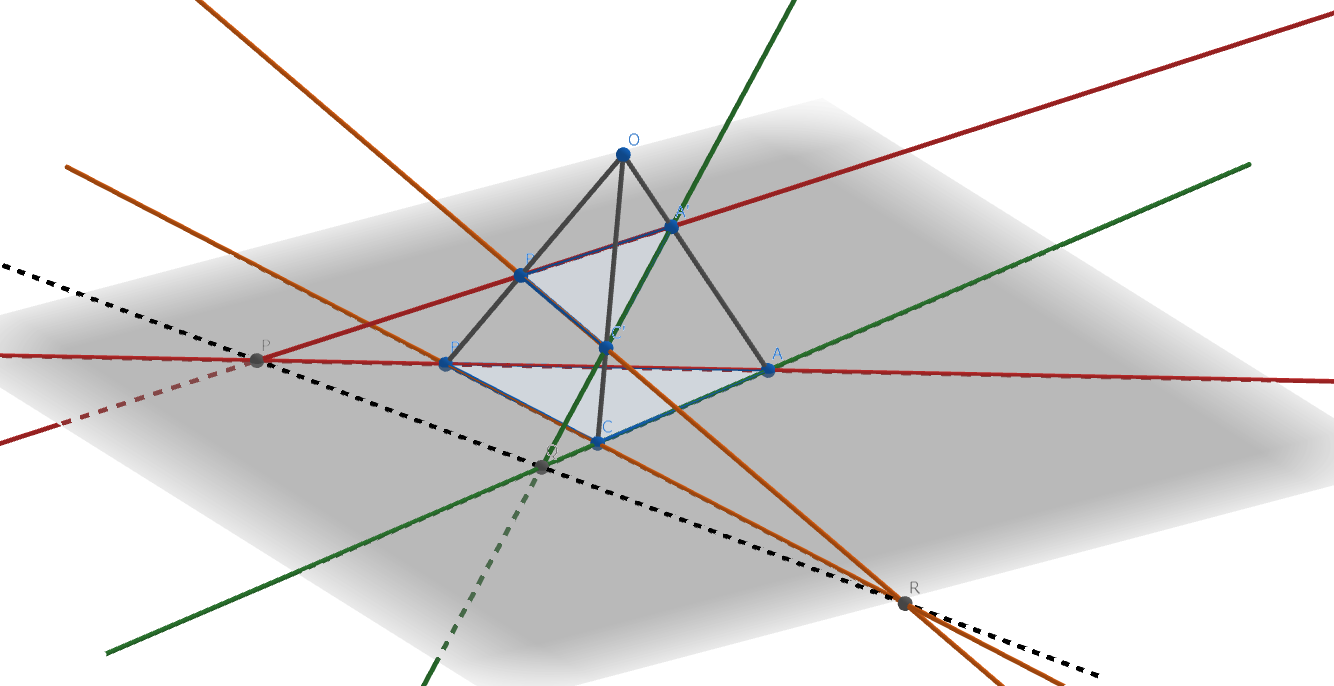
図2.Desarguesの定理 (三次元)-主張
射影の定義とかはこちらを参照してください。
証明 (Menelausの定理による)
まずは初等幾何による解法です。二次元での証明を眺めると、天下り的に見えるかもしれませんが、三次元での証明も併せて見ることでその意図が理解できると思います。こちらも、本質的には射影ですね。
二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
証明
共点を \(O\) とする。このとき、Menelausの定理より、以下を得る。 \[\frac{OA'}{A'A} \cdot \frac{AP}{PB} \cdot \frac{BB'}{B'O} = \frac{OB'}{B'B} \cdot \frac{BQ}{QC} \cdot \frac{CC'}{C'O} = \frac{OC'}{C'C} \cdot \frac{CR}{RA} \cdot \frac{AA'}{A'O} = 1 \]
Menelausの定理の逆を適用する。 \[\frac{AP}{PB} \cdot \frac{BQ}{QC} \cdot \frac{CR}{RA} = 1\] が成り立てば、三点 \(P, \ Q, \ R\) は共線である。一方で、これは以下のように変形できる。 \[ \frac{AP}{PB} \cdot \frac{BQ}{QC} \cdot \frac{CR}{RA} = \frac{A'A}{OA'} \cdot \frac{B'O}{BB'} \cdot \frac{B'B}{OB'} \cdot \frac{C'O}{CC'} \cdot \frac{C'C}{OC'} \cdot \frac{A'O}{AA'} = 1 \] よって、題意は示された。 \(\blacksquare \)
空間内の二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
証明
共点を \(O\) とする。四面体 \(OABC\) の各面についてMenelausの定理を適用する。
・三角形 \(OAB\), \(OBC\), \(OCA\) を含む面を切り取って考える。Menelausの定理より、以下を得る。 \[\frac{OA'}{A'A} \cdot \frac{AP}{PB} \cdot \frac{BB'}{B'O} = \frac{OB'}{B'B} \cdot \frac{BQ}{QC} \cdot \frac{CC'}{C'O} = \frac{OC'}{C'C} \cdot \frac{CR}{RA} \cdot \frac{AA'}{A'O} = 1 \]
三角形 \(ABC\) を含む面で、Menelausの定理の逆を適用する。
\[\frac{AP}{PB} \cdot \frac{BQ}{QC} \cdot \frac{CR}{RA} = 1\] が成り立てば、三点 \(P, \ Q, \ R\) は共線である。一方で、これは以下のように変形できる。 \[ \frac{AP}{PB} \cdot \frac{BQ}{QC} \cdot \frac{CR}{RA} = \frac{A'A}{OA'} \cdot \frac{B'O}{BB'} \cdot \frac{B'B}{OB'} \cdot \frac{C'O}{CC'} \cdot \frac{C'C}{OC'} \cdot \frac{A'O}{AA'} = 1 \] よって、題意は示された。 \(\blacksquare \)
証明 (平行射影による)
Desarguesの定理の射影による解法です。射影についての詳しい記事はこちら。
二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
証明
三次元でのDesarguesの定理を \(A,B,C\) がなす平面に正射影することで、二次元でのDesarguesの定理が得られる。 よって、題意は示された。\(\blacksquare\)
空間内の二つの三角形 \(ABC\) , \(A'B'C'\) において、\(AA', \ BB', \ CC'\) が共点であり、\(AB\) と \(A'B'\) 、 \(BC\) と \(B'C'\) 、 \(CA\) と \(C'A'\) の交点をそれぞれ \(P, \ Q, \ R\) とする。 このとき、\(P,Q,R\) は共線である。
証明
三角形 \(ABC\) を含む面と 三角形 \(A'B'C'\) を含む面の交線を \(l\) とする。このとき、点 \(P\) は直線 \(AB\) 上であり、直線 \(A'B'\) 上でもあるから、直線 \(l\) 上に存在する。 同様に、点 \(Q,R\) についても \(l\) 上にあることが言えるので題意は示された。\(\blacksquare \)
Desarguesの定理の逆と自己双対性
Desarguesの定理は逆も成り立ちます。この証明で最もエレガントなのはDesarguesの定理の双対命題を考えることです。 双対原理についての詳しい記事はこちら(現在執筆中)。
定理の最初の部分は「六点 \(A,B,C,A',B',C'\) において、\(AA',BB',CC'\) が共点である。」と読み替えれば双対命題を取りやすいと思います。
六直線 \(l,m,n,l',m',n'\) において、\(l\) と \(l'\) の交点、\(m\) と \(m'\) の交点、\(n\) と \(n'\) の交点は共線である。 このとき、\(l,m\) の交点と \(l',m'\) の交点がなす直線 \(X\) と、\(m,n\) の交点と \(m',n'\) の交点がなす直線 \(Y\) と、\(n,l\) の交点と \(n',l'\) の交点がなす直線 \(Z\) は共点である。
- 六点 \(A,B,C,A',B',C'\) において、\(AA',BB',CC'\) が共点である。
↓
六直線 \(l,m,n,l',m',n'\) において、\(l\) と \(l'\) の交点、\(m\) と \(m'\) の交点、\(n\) と \(n'\) の交点は共線である。 - \(AB\) と \(A'B'\) の交点 \(P\) と、 \(BC\) と \(B'C'\) の交点 \(Q\) と、 \(CA\) と \(C'A'\) の交点 \(R\) は共線である。
↓
\(l,m\) の交点と \(l',m'\) の交点がなす直線 \(X\) と、\(m,n\) の交点と \(m',n'\) の交点がなす直線 \(Y\) と、\(n,l\) の交点と \(n',l'\) の交点がなす直線 \(Z\) は共点である。
これは、よく見てみるとDesarguesの定理の逆になっています。従って、Desarguesの定理は自己双対な命題などと呼ばれることがあります。
いつ使うべきか?
Desarguesの定理の使いどころについて解説します。 まず、前提として、Desarguesの定理の使用頻はそれほど高くないです。 また、使う場合、その多くは演習問題の問題1のパターンが多いです。 それ以外の場合は、まずは共点が示せていて共線を示したい(共線が示せていて共点を示したい)ときに使うと良いと思います。
ここからは私の偏見ですが、Desarguesの定理をはじめとした、射影幾何学の定理を使う場合は図が大きくなりがちだと感じます。 Desarguesの定理の主張の図を書くときなんかには、うまい角度で書かないと大きくなりすぎてしまうことを感じた人もいるかもしれませんが、これは示したい共線などがそもそも遠くに飛んでしまいやすいことにあります。 ちょっとしたエスパーとして使ってみてください。
演習問題
三角形 \(ABC\) の内部に点 \(P\) が存在し、\(AP,BP,CP\) と \(BC,CA,AB\) の交点をそれぞれ \(D,E,F\) とする。 \(AB\) と \(DE\) の交点を \(X\) 、\(BC\) と \(EF\) の交点を \(Y\) 、\(CA\) と \(FD\) の交点を \(Z\) とするとき、\(X,Y,Z\) は一直線上に存在することを示せ。
これは最も基本的なDesarguesの定理の使い方です。実際の問題では、この問題における点 \(P\) が内心や垂心になることが多いです。
+ 証明を表示/非表示三角形 \(ABC\) において、内心を \(I\) とし、\(\angle{B},\angle{C}\) における傍心を \(I_B,I_C\) とする。 \(BI,CI\) と各辺の交点をそれぞれ \(P_B,P_C\) とするとき、\(AI,I_BP_C,I_CP_B\) が一点で交わることを示せ。
\(AC\) を直径とする円 \(\Gamma\) 上に \(A,C\) とは相異なる点 \(B\) を任意にをとる。点 \( M, N \) は弦 \( AB, BC \) の中点であり、点 \(P,Q\) は劣弧 \(AB, AC\) の中点である。 直線 \( AQ \) と \( BC \) の交点を \( K \) とし、直線 \( CP \) と \( AB \) の交点を \( L \) とするとき、\(MQ, NP, KL\) が一点で交わることを示せ。
三角形 \(ABC\) の辺 \(BC\) 上に点 \(B,C\) とは相異なる点 \(D\) をとり、三角形 \(ABD,ACD\) の外接円と直線 \(AC,AB\) の交点をそれぞれ \(E,F\) とする。 点 \(A\) を直線 \(BC\) に関して対称移動した点を \(A'\) とし、\(A'C,DE\) の交点を \(P\)、\(A'B,DF\) の交点を \(Q\) とするとき、\(AD,BP,CQ\) は共点となる事を示せ。
三角形 \(ABC\) の外心を \(O\) とする。 \(OA,OB,OC\) を直径とする円をそれぞれ \(\omega_1,\omega_2,\omega_3\) とし、\(OBC,OCA,OAB\) の外接円をそれぞれ \(\Gamma_1, \Gamma_2, \Gamma_3\) とする。 \(\omega_1\) と \(\Gamma_1\) の交点を \(P_{1}\) とし、同様に \(P_2,P_3\) についても定めたとき、\(O,P_1,P_2,P_3\) は同一円周上に存在することを示せ。
参考文献
[1] 西山 享, 射影幾何学の考え方(数学のかんどころ 19)