根心の存在定理とその応用
今回は、根心の存在定理について様々な視点から観察し、利用法を模索していきたいと思います。 それでは、よろしくお願いします。
方べきと根軸
点 \(O\) を中心とした半径 \(r\) の円 \(\omega\) と点 \(P\) に対して、\(OP^2-r^2\) を点 \(P\) の円 \(\omega\) に関する方べきという。
方べきは常に正とは限らず、例えば点 \(P\) が円 \(\omega\) の内側にあればその方べきは負になります。
点 \(O_1\) を中心とする半径 \(r_1\) の円 \(\omega_1\) と点 \(O_2\) を中心とする半径 \(r_2\) の円 \(\omega_2\) に対して、円 \(\omega_1,\omega_2\) との方冪が等しいような点の軌跡を根軸という。 ただし、\(\omega_1,\omega_2\) の中心は相異なるものとする。
根軸は、中心が異なる二円に対してのみ定義されます。
根軸は直線である。
証明
\[\omega_1 : (x-a_1)^2 + (y-b_1)^2 = r_1^2 , \ \omega_2 : (x-a_2)^2 + (y-b_2)^2 = r_2^2\] とする。また、\(P(X,Y)\) とする。このとき、根軸の定義より、以下の式が成り立つ。 \[(X-a_1)^2 + (Y-b_1)^2 - r_1^2 = (X-a_2)^2 + (Y-b_2)^2 - r_2^2\] これらを整理することで、以下の式を得る。 \[2(a_1-a_2)X + 2(b_1-b_2)Y = (a_1^2-a_2^2) + (b_1^2-b_2^2) - (r_1^2-r_2^2) \ \ \ \cdots (*)\] 円 \(\omega_1,\omega_2\) は中心が異なるから \((a_1,b_1) \not= (a_2,b_2)\) である。よって、\((*)\) は直線の式となる。以上より、題意は示された。\(\blacksquare\)
根軸は二円の中心を結ぶ直線と直行する。
証明
文字や座標を補題1と同様に設定する。 このとき、二円の中心を結ぶ直線の傾きは \(\frac{b_1-b_2}{a_1-a_2}\) で与えられる。 \((*)\) より、根軸の傾きは \(-\frac{a_1-a_2}{b_1-b_2}\) で与えられるため、一次関数の直行条件を考えれば根軸と二円の中心を結ぶ直線は直行することが分かる。\(\blacksquare\)
相異なる二点 \(P,Q\) で交わる二円 \(\omega_1,\omega_2\) の根軸は直線 \(PQ\) である。
証明
補題3より、根軸は二円の中心を結ぶ直線に直行する。 \(P,Q\) は二円の方べきが共に \(0\) になる点であるから、直線 \(PQ\) が根軸である。 \(\blacksquare\)
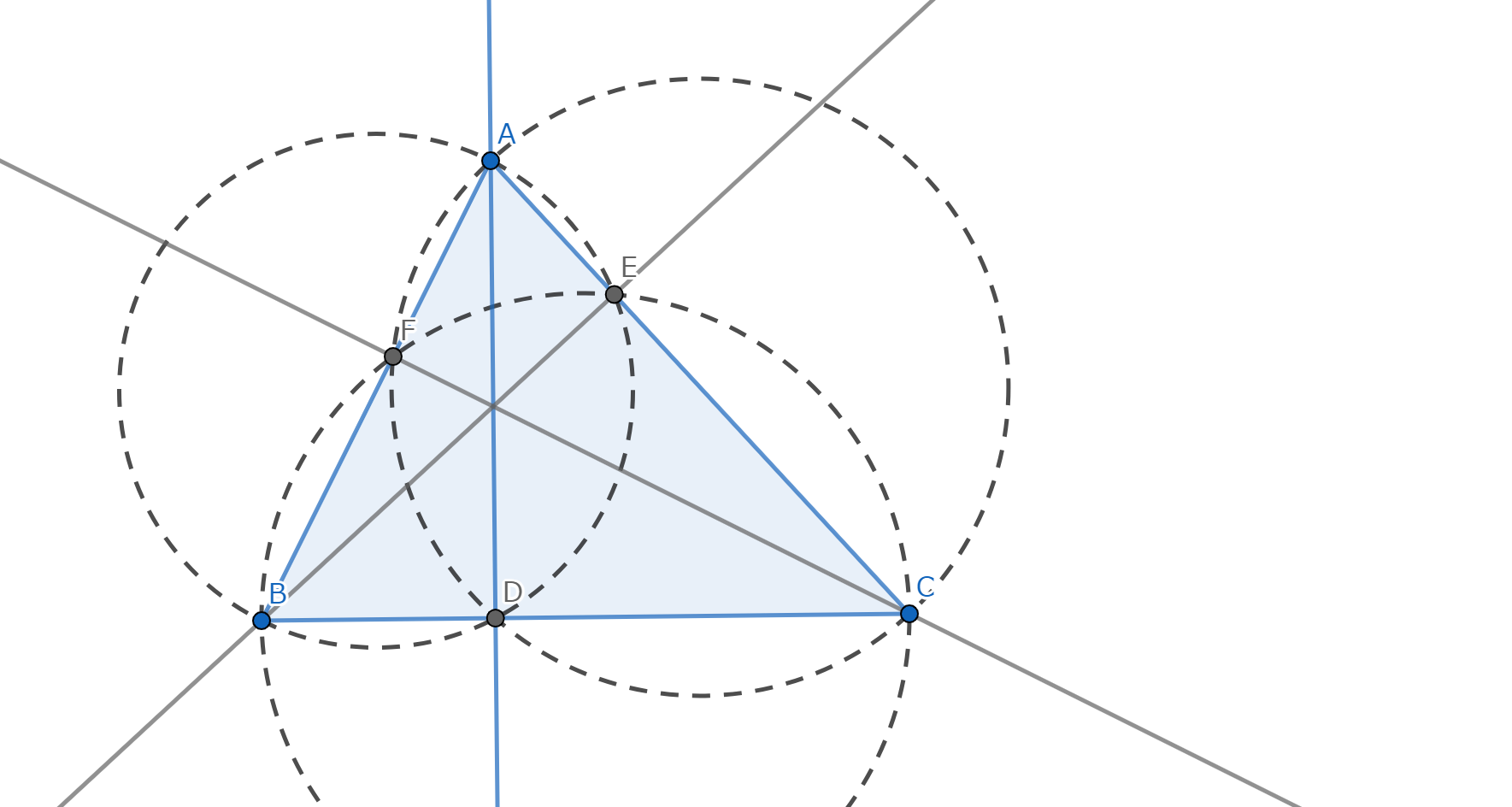
点 \(O\) を中心とする半径 \(r\) の円 \(\omega\) と点 \(P\) があり、直線 \(l\) が点 \(P\) を通り円 \(\omega\) と二点 \(A,B\) で交わっている。(\(A=B\) の場合は接していると考える。) このとき、 \[PA \cdot PB = \left|OP^2-r^2 \right| = \mathrm{const} \] が常に成り立つ。
証明
点の位置関係によって、場合分けをします。
点 \(P\) が外部にある場合
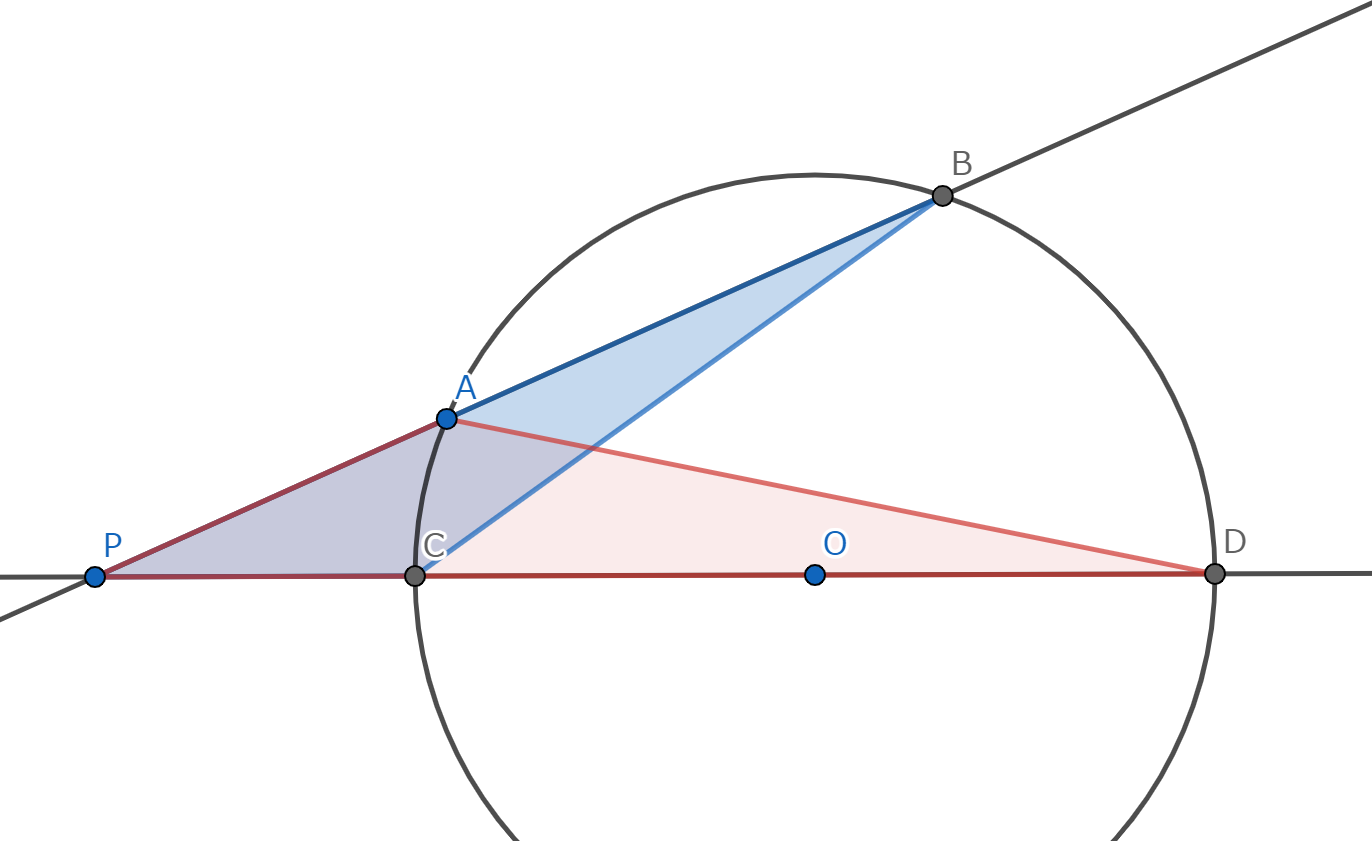
図1.方べきの定理1
接する場合については、接弦定理を用いればよいです。
点 \(P\) が内部にある場合
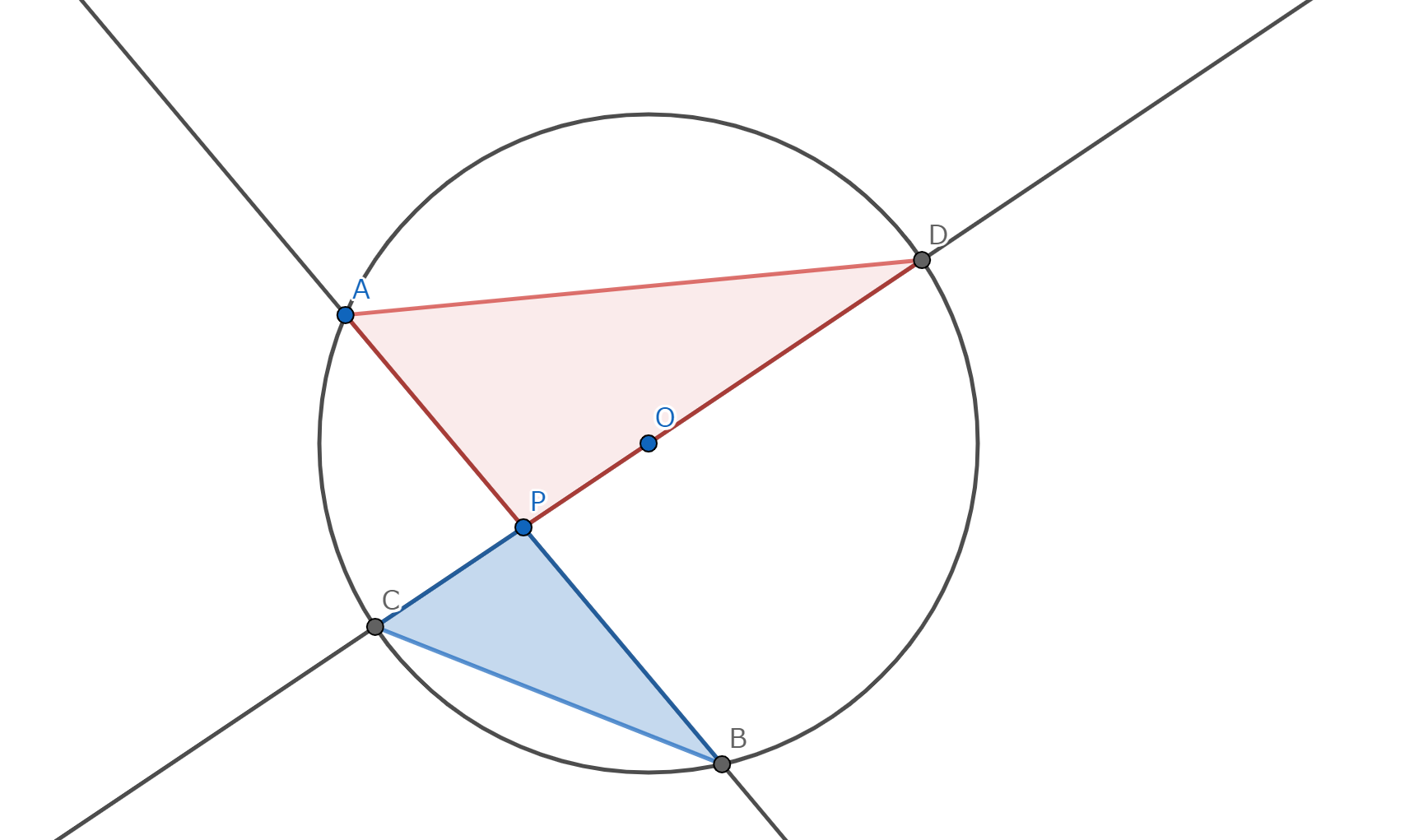
図2.方べきの定理2
主張
それでは、本題です。
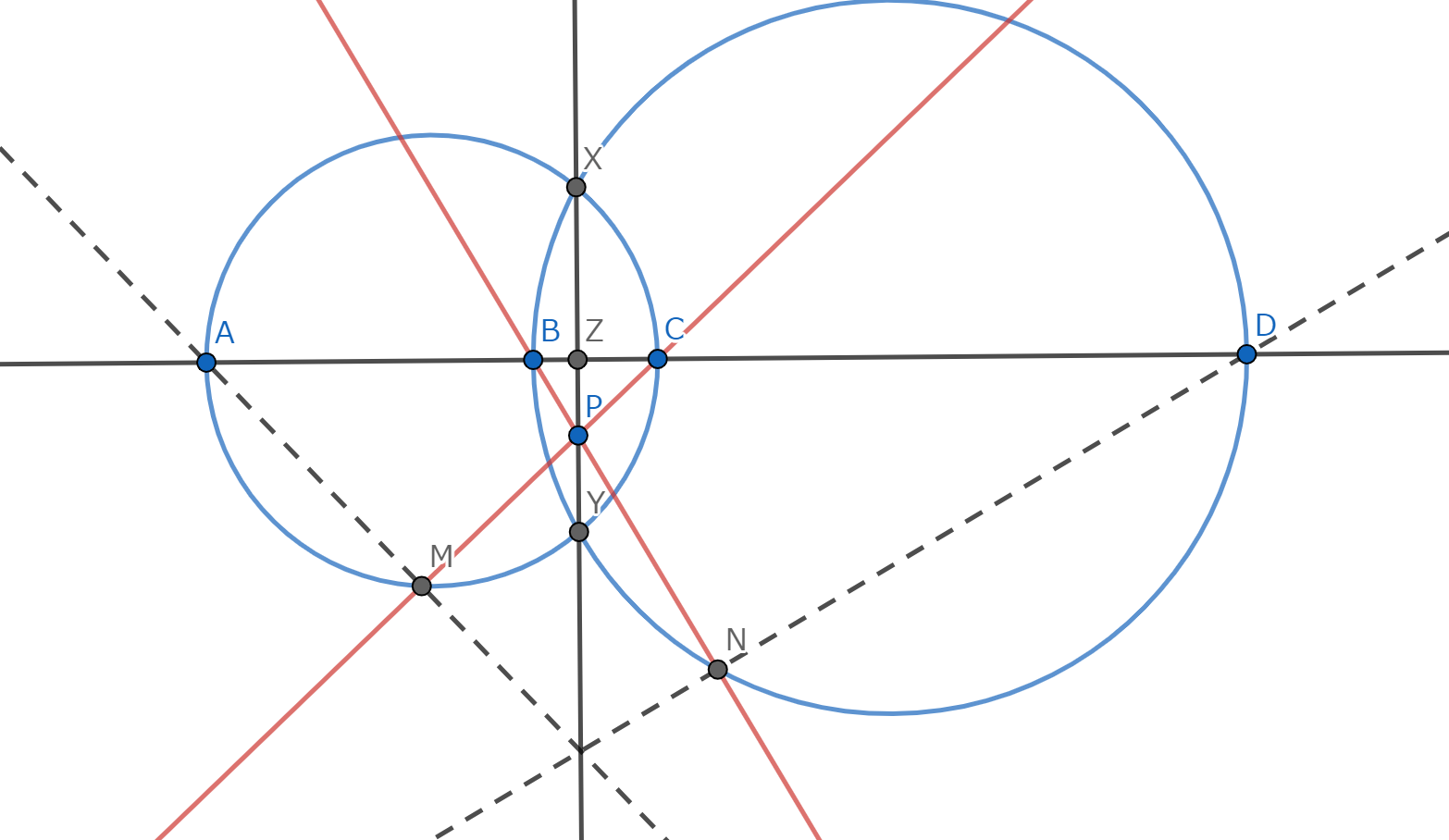
三円 \(\omega_1,\omega_2,\omega_3\) があり、\(\omega_1,\omega_2\) 、 \(\omega_2,\omega_3\) 、 \(\omega_3,\omega_1\) の根軸をそれぞれ \(l_{12},l_{23},l_{31}\) とすると、 \(l_{12},l_{23},l_{31}\) は一点で交わる。
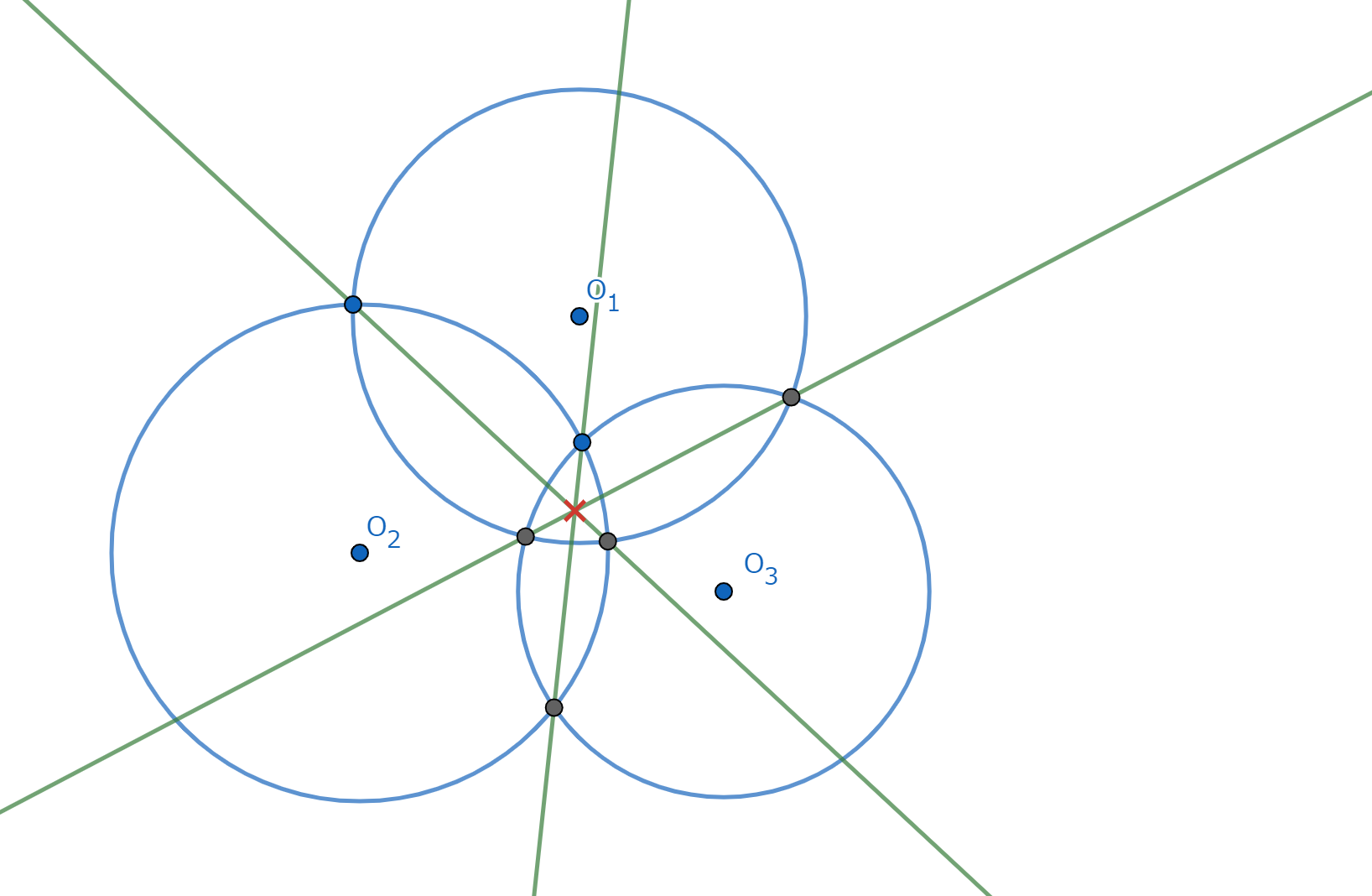
図3.三円の根心
根心の存在定理は、反転、相似中心関連の定理と並んで円が複数登場する問題の三種の神器です。合言葉は「渾身の根心」です。
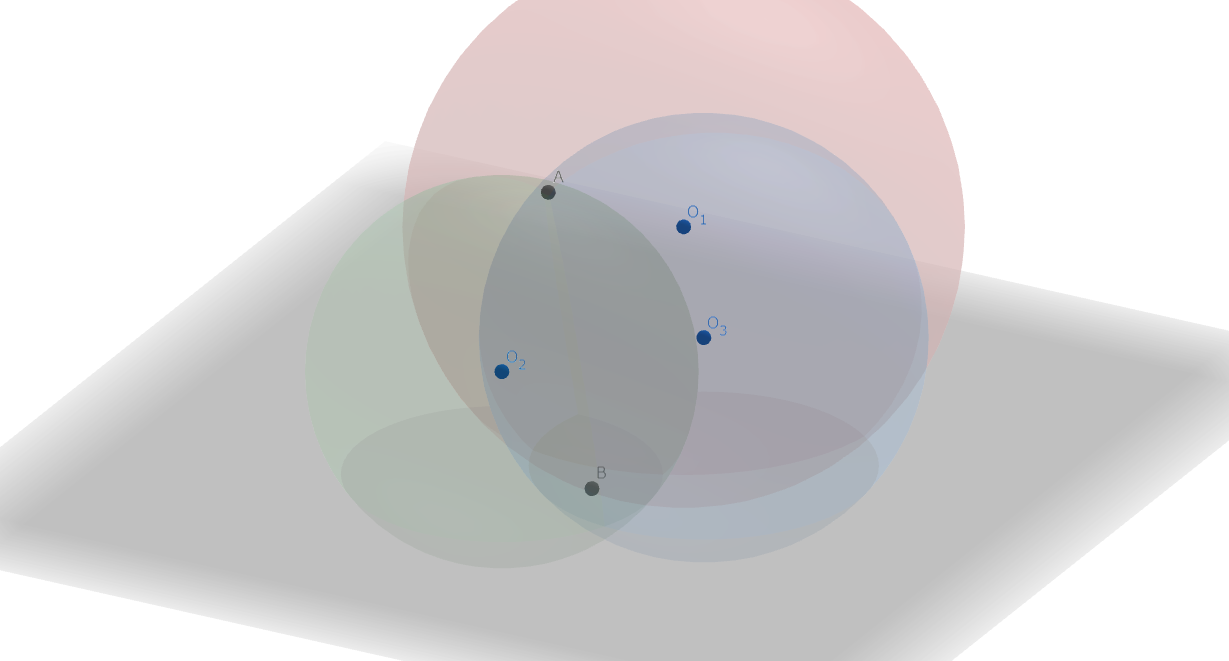
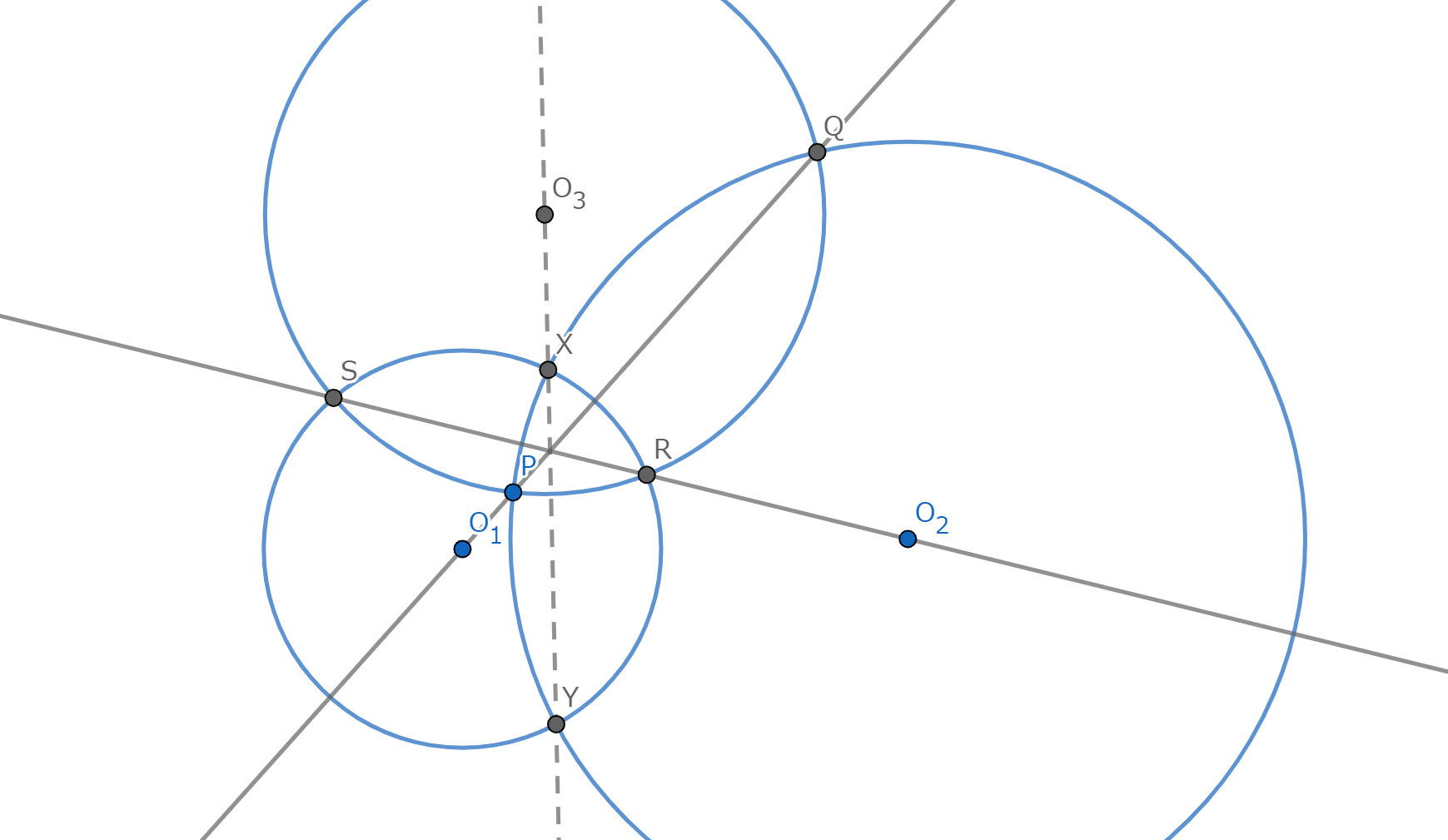
図4.三球の共点
証明 (方べきの定理による)
三円 \(\omega_1,\omega_2,\omega_3\) があり、\(\omega_1,\omega_2\) 、 \(\omega_2,\omega_3\) 、 \(\omega_3,\omega_1\) の根軸をそれぞれ \(l_{12},l_{23},l_{31}\) とすると、 \(l_{12},l_{23},l_{31}\) は一点で交わる。
証明
三円の半径をそれぞれ \(r_1,r_2,r_3\) 、中心を \(O_1,O_2,O_3\) とする。 根軸の定義から、\(l_{12}\) 上の点 \(P\) は \(O_1P^2 -r_1^2 = O_2P^2 - r_2^2\) を満たす。 同様に、\(l_{23}\) 上の点 \(P\) は \(O_2P^2 - r_2^2 = O_3P^2 - r_3^2\) を満たす。 ここで、\(l_{12},l_{23}\) の交点を \(O\) とすれば、点 \(O\) は \(OO_1^2 - r_1^2 = OO_2^2 - r_2^2 = OO_3^2 - r_3^2\) を満たす。 よって、\(O\) は \(l_{31}\) 上にも存在するから、題意は示された。 \(\blacksquare\)
証明の逆にたどることで、逆が成り立つこともわかります。
証明? (平行射影による)
恐らく全く厳密でないと思いますが、お気持ちを伝えておきます。射影の定義とかはこちら。
三円 \(\omega_1,\omega_2,\omega_3\) があり、\(\omega_1,\omega_2\) 、 \(\omega_2,\omega_3\) 、 \(\omega_3,\omega_1\) の根軸をそれぞれ \(l_{12},l_{23},l_{31}\) とすると、 \(l_{12},l_{23},l_{31}\) は一点で交わる。
証明
三円を断面に持つような球 \(\omega_1',\omega_2',\omega_3'\) をそれぞれ考える。ただし、三球の中心は 三円が存在する円に関して同じ側にあり、三球はある二点を共有する。 補題3より、二つの球の共通の断面を含む平面を三円が存在する平面に射影した直線が根軸であることがわかる。 一方で、後述の定理3より、三球はある二点で交わるから題意は示された。 \(\blacksquare\)根心の存在定理の"自己反転性"
根心の存在定理の反転を考えてみます。 適当な二円の交点の一つを中心として反転してみましょう。一点で交わる三直線 \(l_1,l_2,l\) があり、直線 \(l_1\) 上に 点 \(P_1,Q_1\) 、直線 \(l_2\) 上に点 \(P_2,Q_2\) 、直線 \(l\) 上に点 \(O\) がある。 四点 \(P_1,P_2,Q_1,Q_2\) が共円であるとき、円 \(OP_1Q_1,OP_2Q_2\) は直線 \(l\) 上で交わる。
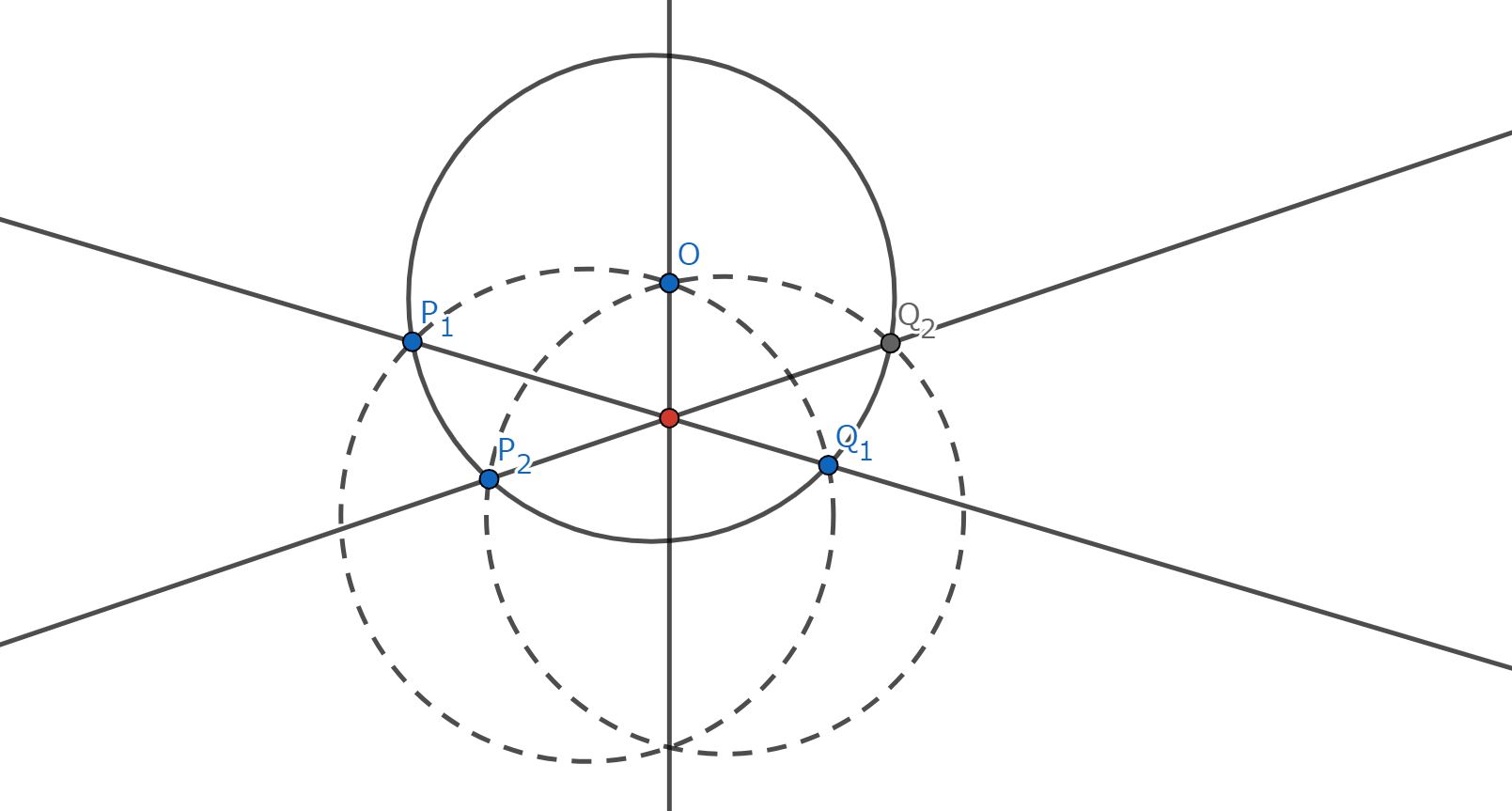
図5.根心の存在定理の反転
なんと、似たような命題が得られました。とても面白いですね!なんとなく、これを"自己反転性"とでも呼ぶことにします。
いつ使うべきか?
お行儀よく三円が分かりやすく出てきてくれるケースは少ないです。 円が出てくるというよりは共円な四点がたくさん出てくるというケースが多いです。 したがって、共円な四角形を探していくことが大切になってきます。
もちろん、円がたくさん出てくる問題でも頻繁に使います。 ですが、根心だけで完結することは少なく、反転や相似中心も使います。 これらの道具も使えるようにしておきましょう。
あと、これは裏技ですが円を極限まで小さくして点にしてしまうと面白いことが起きます。稀に刺さります。
演習問題
演習問題で使い方を確認していきましょう。
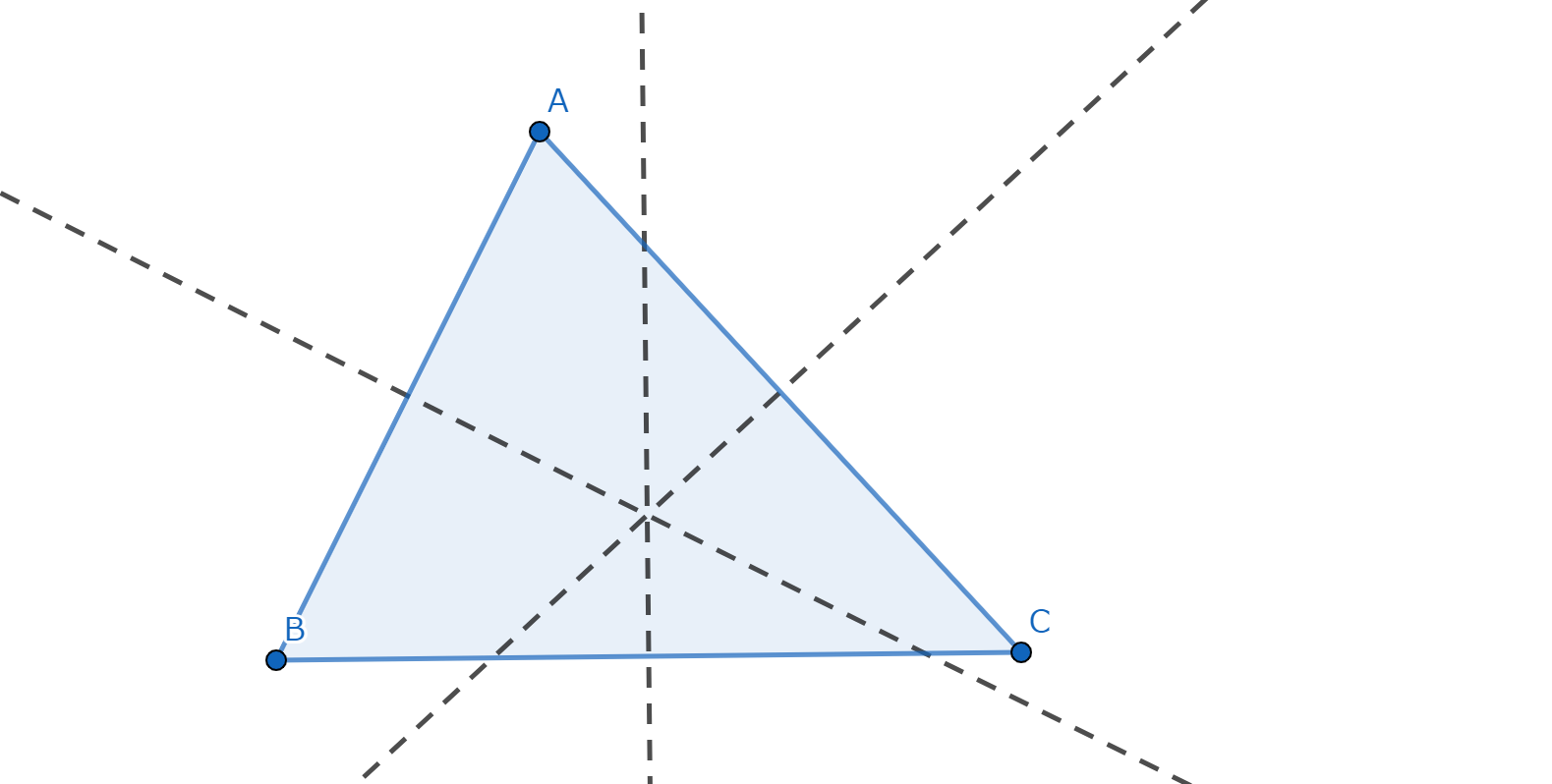
三角形 \(ABC\) において、各頂点から対辺へと降ろした垂線は一点で交わることを示せ。
三角形 \(ABC\) において、各辺の垂直二等分線は一点で交わることを示せ。
相異なる二点 \(A,B\) で交わる二円 \(C_1,C_2\) が平面上にあります。 これらの共通接線のひとつを \(l\) とし、その \(C_1,C_2\) との接点をそれぞれ \(P,Q\) とするとき、以下の式が成り立ちました。 \[AP = 5 ,\ AQ = 7 , PQ = 6 \] このとき、線分 \(AB\) の長さを求めよ。
これはやや重要です。構図のようなものです。
証明を表示/非表示三角形 \(ABC\) において、各頂点に対する傍接円をそれぞれ \(\omega_A,\omega_B,\omega_C\) とする。 このとき、三円 \(\omega_A,\omega_B,\omega_C\) の根心は三角形 \(ABC\) の中点を結んでできた三角形の内心であることを示せ。
四点 \(A,B,C,D\) が直線 \(l\) 上に存在し、\(AC,BD\) を直径とするような二円 \(\omega_1,\omega_2\) が点 \(X,Y\) で交わっている。 直線 \(XY\) 上にあり、\(l\) 上にない点 \(P\) があり、\(CP,BP\) と \(\omega_1,\omega_2\) の交点のうち、名前がついていないものをそれぞれ \(M,N\) とするとき、\(XY,AM,DN\) が共点となることを示せ。
きほんの「き」ですね。
証明を表示/非表示\(O_1,O_2\) を中心とする二円 \(\Gamma_1,\Gamma_2\) が二点 \(X,Y\) で交わっている。 \(O_1\) を通る直線が、\(\Gamma_1\) と \(P,Q\) で交わり、\(O_2\) を通る直線が \(\Gamma_2\) と \(R,S\) で交わる。 \(P,Q,R,S\) が共円の場合に、その円の中心が直線 \(XY\) 上に存在することを示せ。
次の問題は、難しいというよりも頻出な構図になっています。
外接円を \(\Omega\) とする三角形 \(ABC\) において、各頂点から対辺への垂線の足をそれぞれ \(H_A,H_B,H_C\) とし、垂心を \(H\) とする。 \(AH\) を直径とする円 \(\omega\) と \(\Omega\) の交点のうち \(A\) でないものを \(P\) とするとき、\(AP,BC,H_BH_C\) は共点であることを示せ。
ここまでは、基本です。最後はかなり難しい問題になっています。頑張ってください。解説は書いている途中なので、かわりにAoPSのリンクを貼っておきます。
外接円を \(\Omega\) とする三角形 \(ABC\) の内心を \(I\) とする。直線 \(AI\) は \(BC\) と \(D\) で交わり、\(\Omega\) と \(M (\not=A)\) で交わる。 直径を \(DM\) とする円が \(\Omega\) と \((K\not=M)\) で交わる。直線 \(MK,BC\) の交点を \(S\) とし、線分 \(IS\) の中点を \(N\) とする。 三角形 \(KID\) 、\(MAN\) の外接円の交点を \(L_1,L_2\) とするとき、線分 \(IL_1,IL_2\) の中点のうち、どちらか一方が \(\Omega\) 上に存在することを示せ。
参考文献
[1] マスオ:根心の性質と根心の存在定理 , 高校数学の美しい物語 , https://manabitimes.jp/math/696
[2] ナキイルカ:シュピーカー中心 , 新ユークリッド幾何学 , https://kikagaku.at-ninja.jp/triangle_geometry/Spieker_center.html