三角形の五心とその性質

今回は、三角形の五心の基本性質について詳しく解説していきます。 今回扱うのは、あくまで基本性質であり、競技数学的構図はまた詳しく別の記事で扱います。 それでは、よろしくお願いします。

五心の存在性

重心

証明

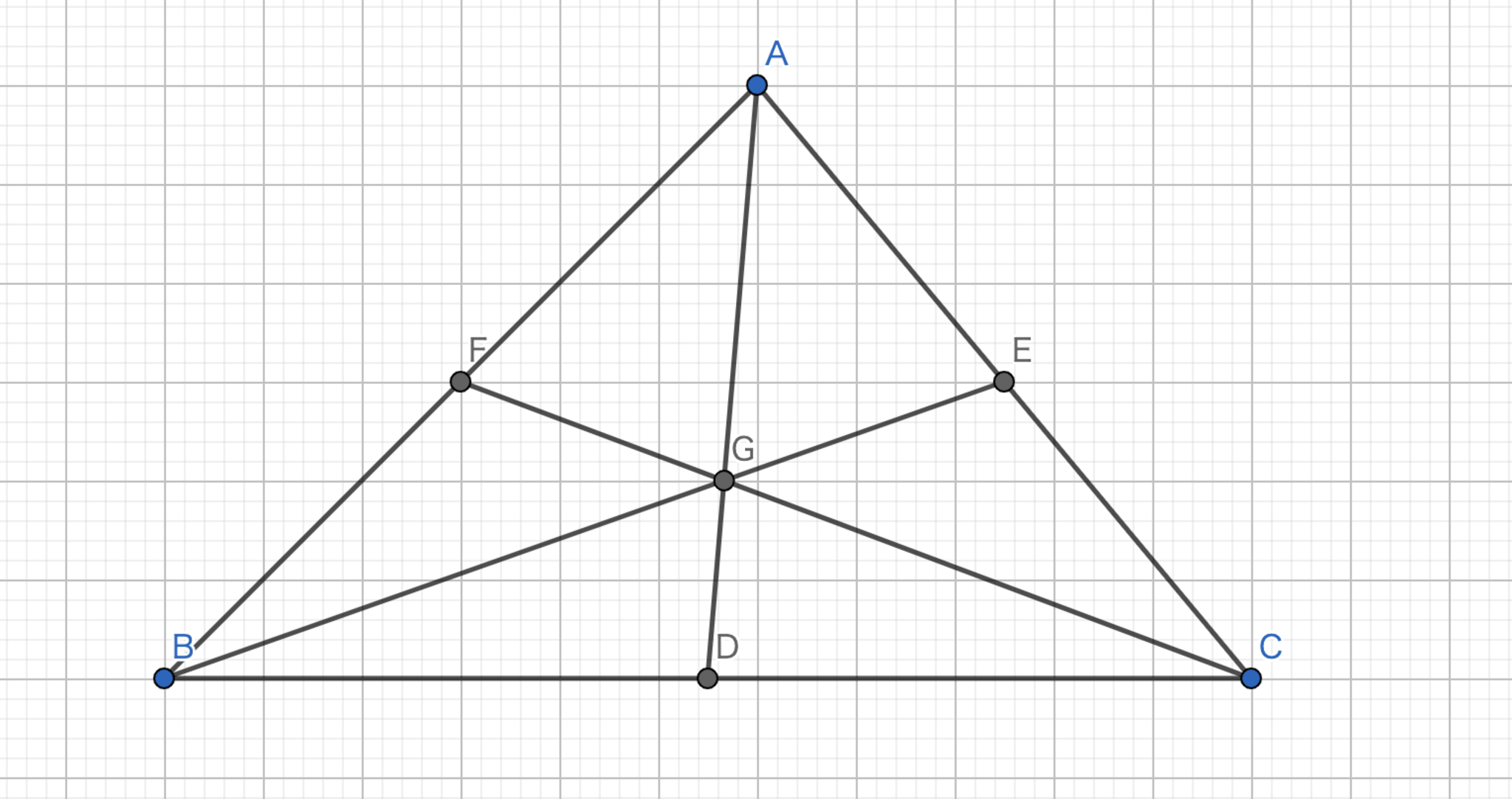
図1.重心

三角形 \(ABC\) の各辺の中点を \(D,E,F\) とすれば、チェバの定理の逆より \(\frac{|AF|}{|FB|} \cdot \frac{|BD|}{|DC|} \cdot \frac{|CE|}{|EA|}\) = 1 であるから一点で交わる。\(\blacksquare\)

内心

証明 (チェバの定理を利用)

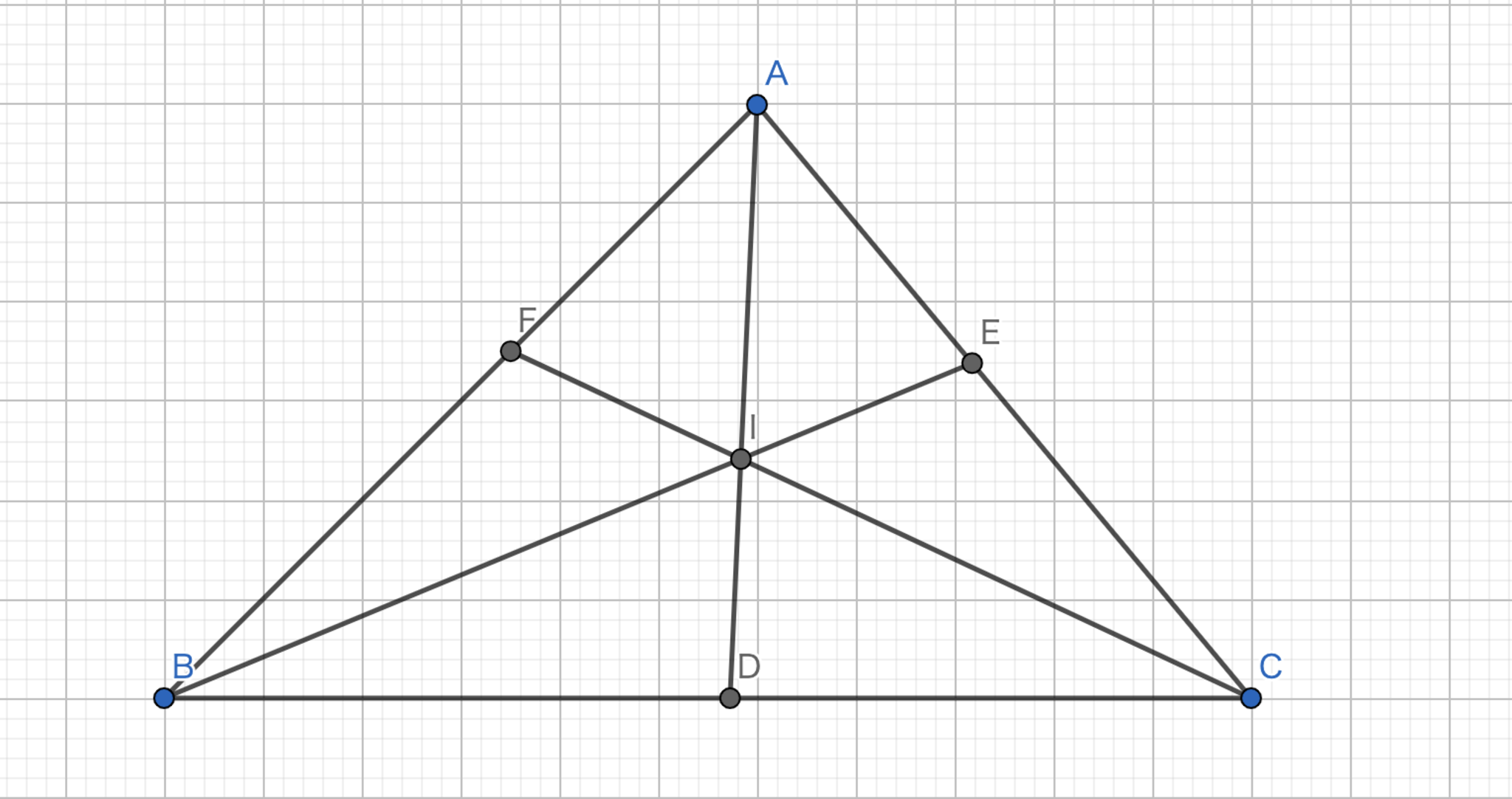
図2.内心1

三角形 \(ABC\) において、角 \(A\) の二等分線と対辺の交点を \(D\)、角 \(B\) の二等分線と対辺の交点を \(E\)、角 \(C\) の二等分線と対辺の交点を \(F\) とすれば、チェバの定理の逆より、\(\frac{|AF|}{|FB|} \cdot \frac{|BD|}{|DC|} \cdot \frac{|CE|}{|EA|}\) = \(\frac{|CA|}{|BC|} \cdot \frac{|AB|}{|CA|} \cdot \frac{|BC|}{|AB|}\) = 1 であるから一点で交わる。 \(\blacksquare\)

証明 (合同を利用)

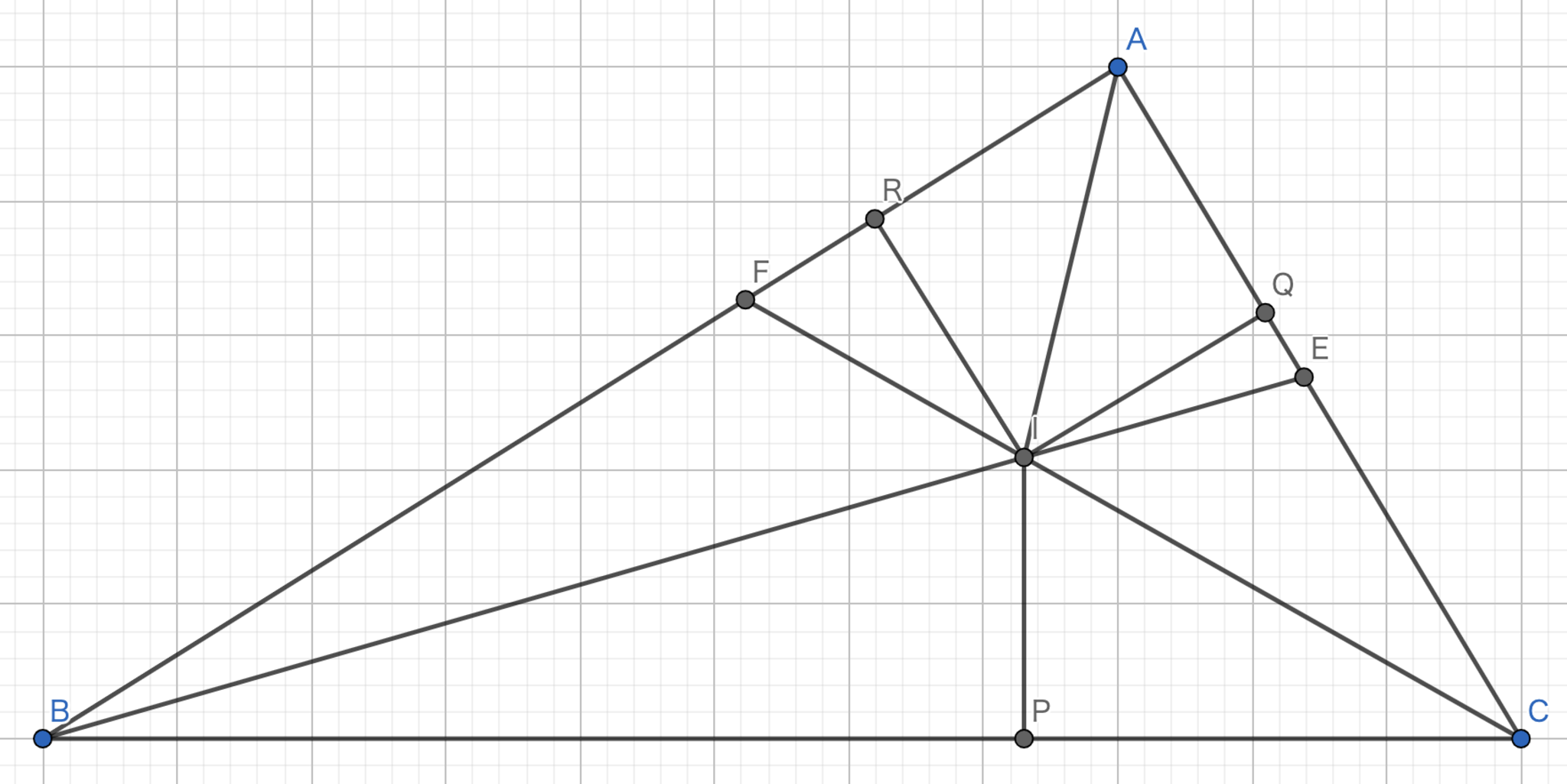
図3.内心2

方針：まず二つの角の二等分線の交点を考え、その交点と残りの頂点を結ぶ線が角の二等分線であることを示す。

　三角形 \(ABC\) において、角 \(B\) の二等分線と角 \(C\) の二等分線の交点を \(I\) とする。\(I\) から各辺へ下ろした垂線の足をそれぞれ \(P, Q, R\) とする。（図を参照） ここで、\(\angle RBI = \angle PBI\)、\(\angle BPI = \angle BRI = 90°\) であり、\(BI\) が共通であるため \(\triangle RBI \equiv \triangle PBI\) が成り立つ。よって、\(|RI| = |PI|\) である。同様に、\(|QI| = |PI|\) が得られる。このことから \(|RI| = |QI|\) である。 \(\angle ARI = \angle ARI = 90°\)、\( |RI| = |QI|\) であって、\(AI\) が共通なので \(\triangle ARI \equiv \triangle AQI\) となる。よって、\(\angle IAR = \angle IAQ\) が従う。このことより、線分 \(AI\) は角 \(A\) の二等分線であることが示された。 \(\blacksquare\)

内心は、内接円の中心ですね。

外心

証明

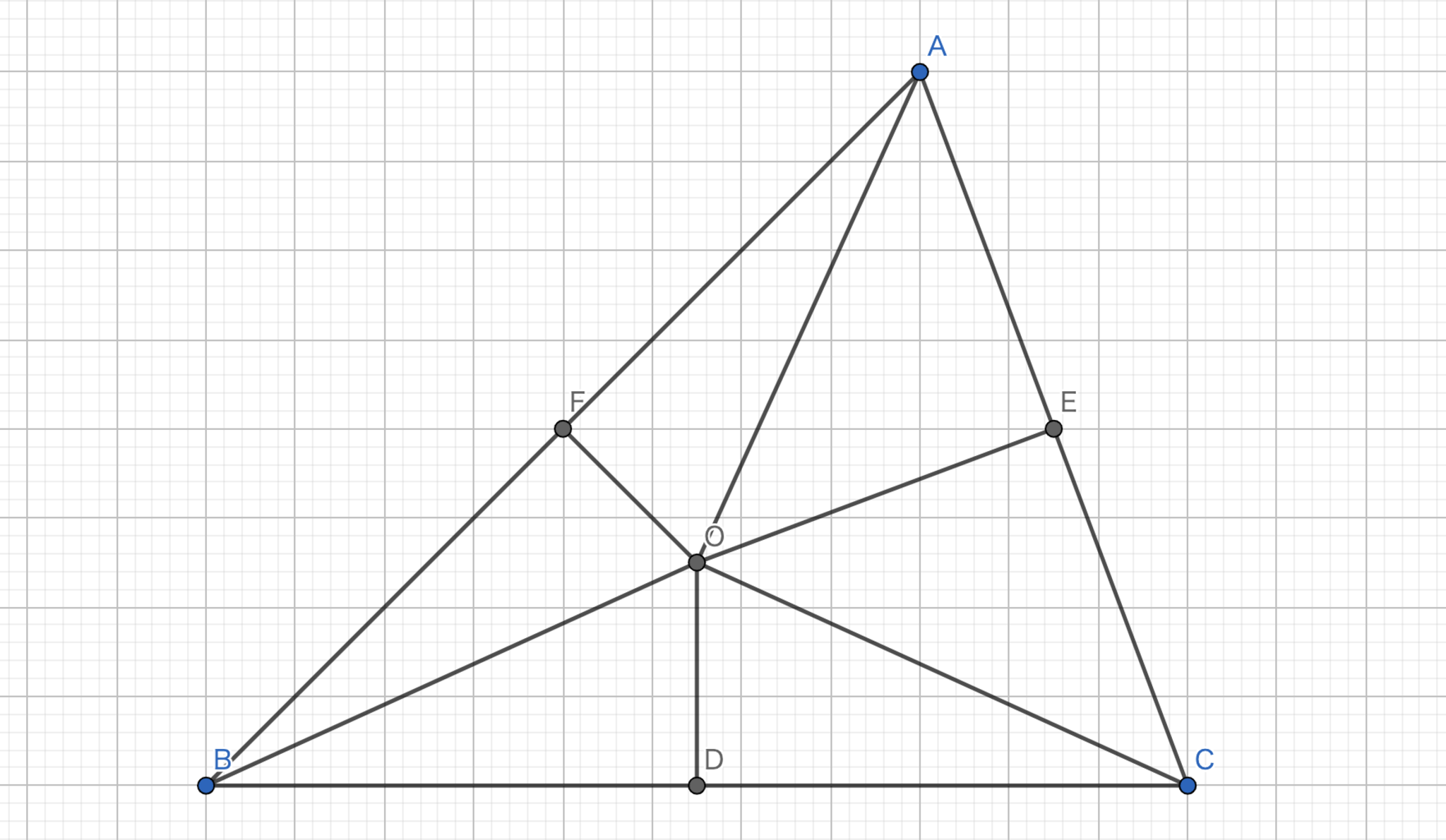
図4.外心

方針：まず二つの辺の垂直二等分線の交点を考えその交点から残りの辺への垂線を下ろす。\(\) その点が中点であることを示す。

　\(AB\)の垂直二等分線と\(CA\)の垂直二等分線の交点を\(O\)とする。\(O\)から\(BC\)へ下ろした垂線の足を\(D\)とする。また、\(AB,CA\)の中点を\(F,E\)とする。 ここで、\(F\)は\(AB\)の中点であるから、\(|AF|=|FB|\)である。また、\(\angle AFO= \angle BFO = 90°\)で\(OF\)が共通なので、\(\triangle AFO\) と \(\triangle BFO\) は合同である。同様に、\(\triangle AEO\) と \(\triangle CEO\) は合同である。このことから、\(|OB|=|OC|\)が従う。よって、三角形\(OBC\)は二等辺三角形である。二等辺三角形の頂角から下ろした垂線は底辺の中点と交わるので\(D\)は\(BC\)の中点である。よって、\(OD\)は垂直二等分線であるから題意は示された。 \(\blacksquare\)

垂心

証明 (角度追跡を利用)

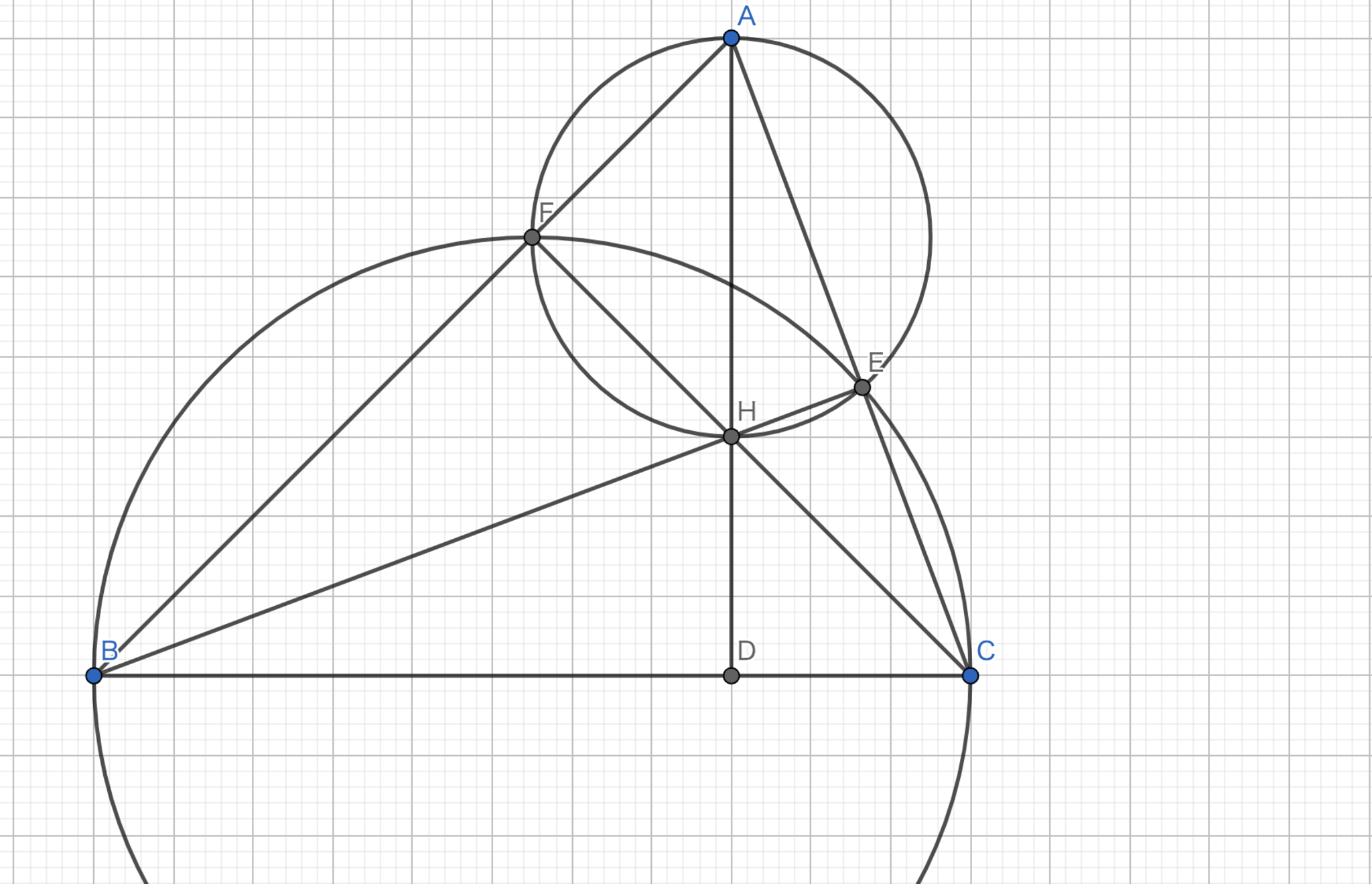
図5.垂心1

方針：共円の存在を利用して角度計算をして示す。

　\(B\)から\(CA\)へと下ろした垂線の足を\(E\)とする。同様に\(C\)から\(AB\)へと下ろした垂線の足を\(F\)とする。\(A\)と\(H\)を通る直線と\(BC\)との交点を\(D\)とする。 \(\angle AFH = \angle AEH = 90°\) であるので、\(AFHE\) は共円である。このことから円周角の定理より、\(\angle FAH = \angle FEH = \angle FCB\) が従う。\(\angle ADB = 180° - \angle BED - \angle ABD = 180° - \angle FCB - \angle ABD = 180° - \angle FCB - (180° - 90° - \angle BAD) = 90°\) よって、\(AD\) は垂線であるから題意は示された。 \(\blacksquare\)

証明 (外心の存在性を利用)

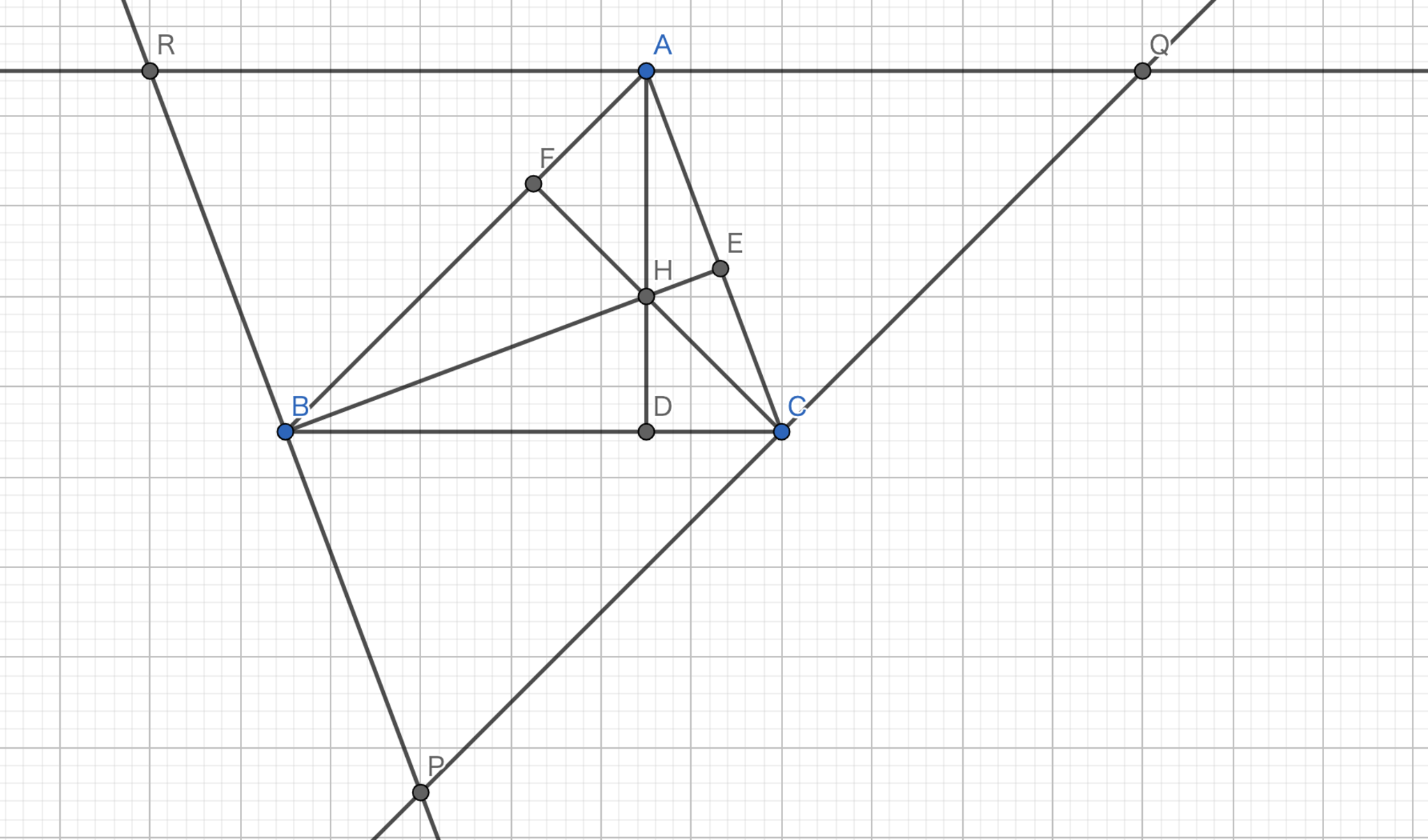
図6.垂心2

方針: 外心の存在を利用する。

　各頂点を通り、対辺に並行な直線をそれぞれ引く。それらの交点を図のように \(P, Q, R\) とする。すると、中点連結定理より、\(A\) は \(QR\) の中点になる。同様に、\(B, C\) はそれぞれ \(RP, PQ\) の中点になる。また、\(QR\) が \(BC\) に平行であるから、\(AD \perp QR\) である。したがって、\(AD\) は \(QR\) の垂直二等分線である。同様に、\(BE, CF\) はそれぞれ \(RP, PQ\) の垂直二等分線である。このことから、\(H\) は三角形 \(PQR\) の外心である。定理3（外心の存在）より、題意は示された。 \(\blacksquare\)

傍心

傍心は一つの三角形に対して、三つ存在します。

証明

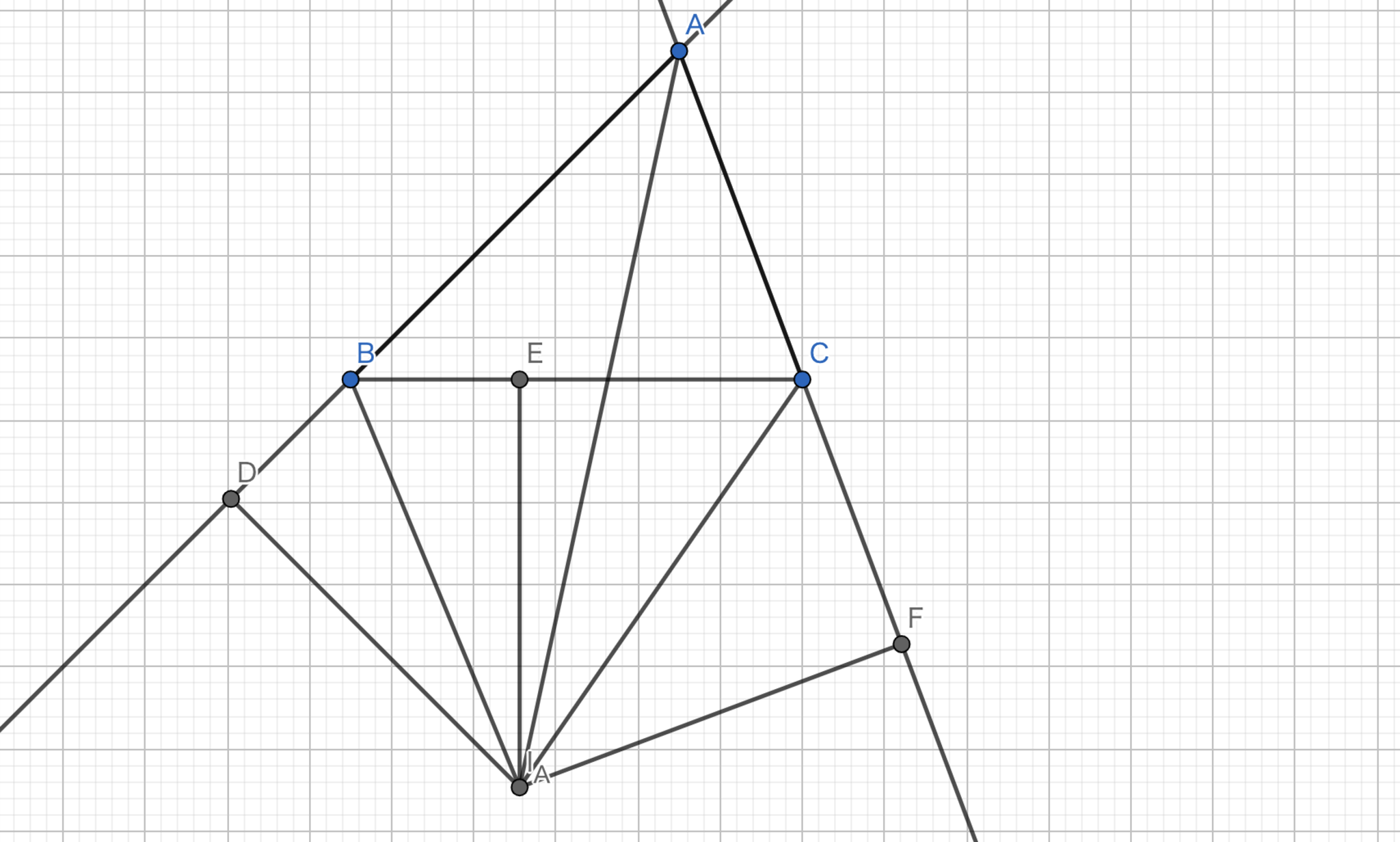
図7.傍心

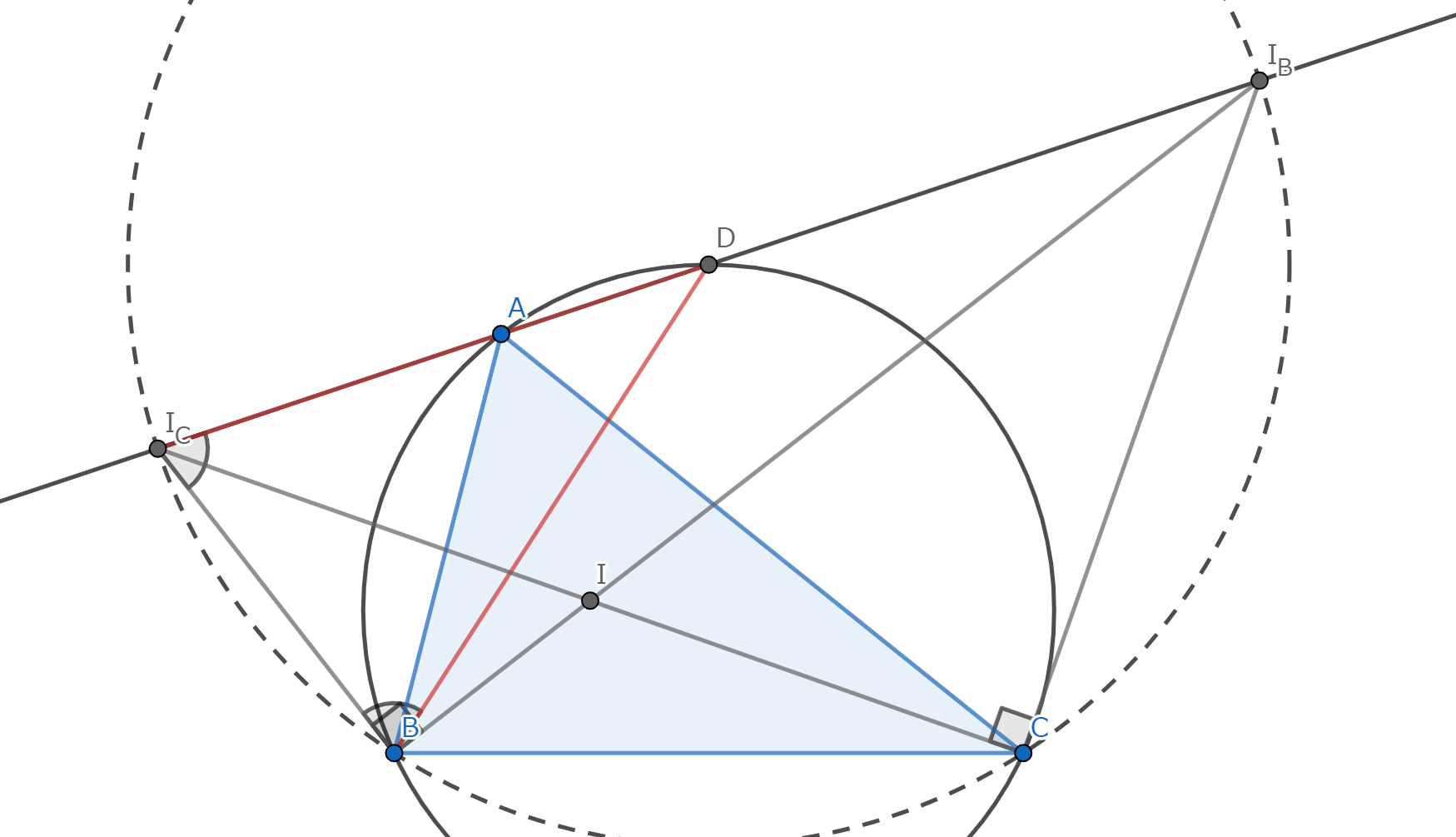
方針：外角の二等分線の交点と \(A\) を結んだ線分が角 \(A\) の内角の二等分線であることを示す。 (傍心は内心とほぼ一緒です。)

　\(I_{A}\) から \(AB, BC, AC\) へと垂線を下ろす。その足をそれぞれ \(D, E, F\) とする。 \(\angle DBI_{A} = \angle EBI_{A}\) であり、\(\angle BDI_{A} = \angle BEI_{A} = 90°\) で \(BI_{A}\) が共通であるから、\(\triangle DBI_{A} \equiv \triangle EBI_{A}\) である。同様に、\(\triangle FCI_{A} \equiv \triangle ECI_{A}\) である。よって、\(|DI_{A}| = |EI_{A}| = |FI_{A}|\) が従う。 \(\angle ADI_{A} = \angle AFI_{A} = 90°\) であり、\(|DI_{A}| = |FI_{A}|\) で \(AI_{A}\) が共通であるから \(\triangle ADI_{A} \equiv \triangle AFI_{A}\) である。従って、\(AI_{A}\) は角 \(A\) の内角の二等分線である。題意は示された。 \(\blacksquare\)

五心関連の長さ

証明

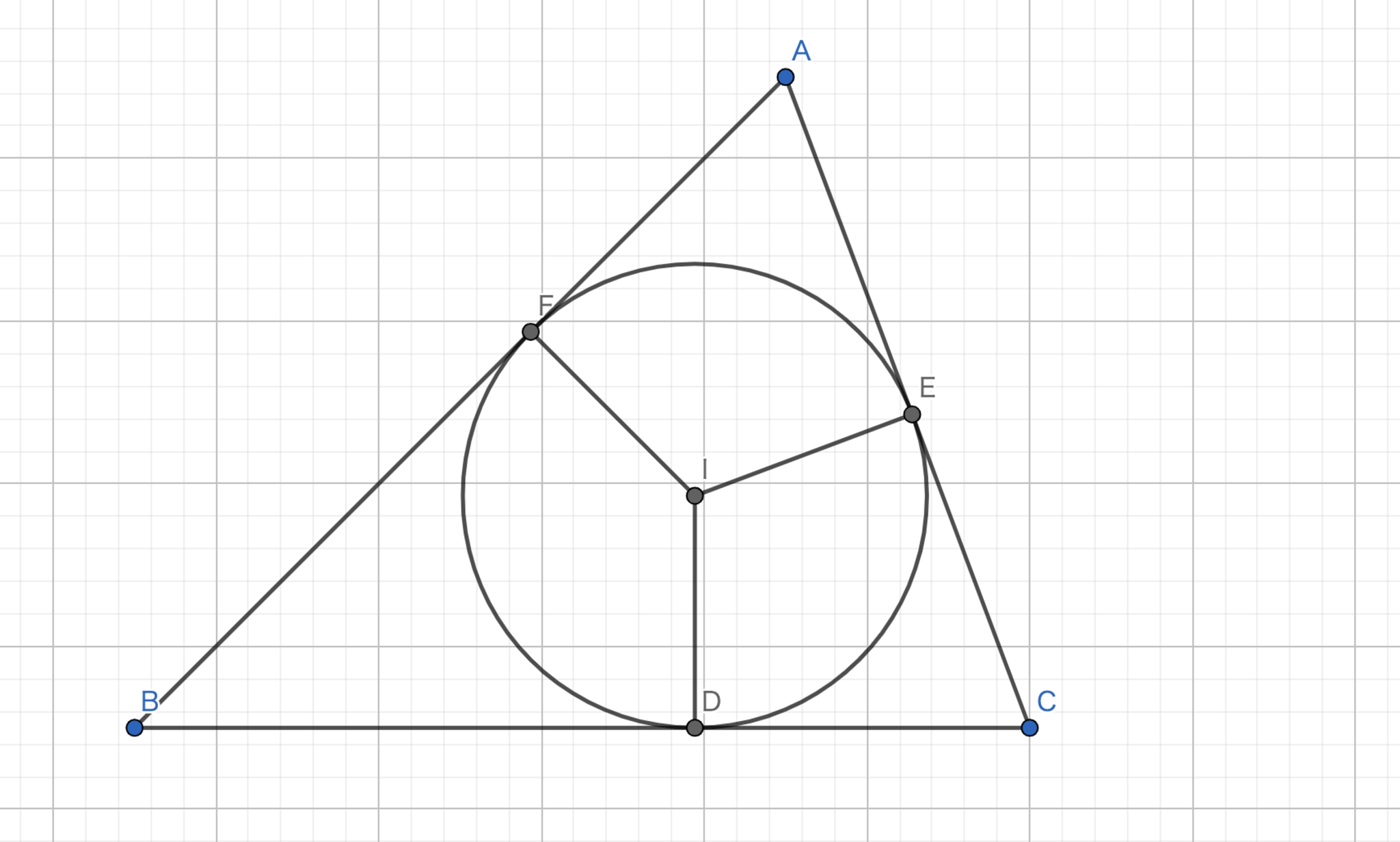
図8.内接円の半径

三角形\(ABC\)の面積を\(S\)とすると、\(S = \frac{r(a+b+c)}{2}\) である。これを \(r\) について解くと、\(r = \frac{2S}{a+b+c}\) が得られる。また、\(S\) をヘロンの公式を用いて \(a, b, c\) で表すと、 \[ \begin{align*} r & = \frac{2\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)\left(\frac{a-b+c}{2}\right)\left(\frac{a+b-c}{2}\right)}}{a+b+c} \\ & = \sqrt{\frac{4(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{16(a+b+c)^{2}}} \\ & = \frac{1}{2}\sqrt{\frac{(-a+b+c)(a-b+c)(a+b-c)}{a+b+c}} \end{align*} \] となって、最右辺が得られる。\(\blacksquare\)

証明

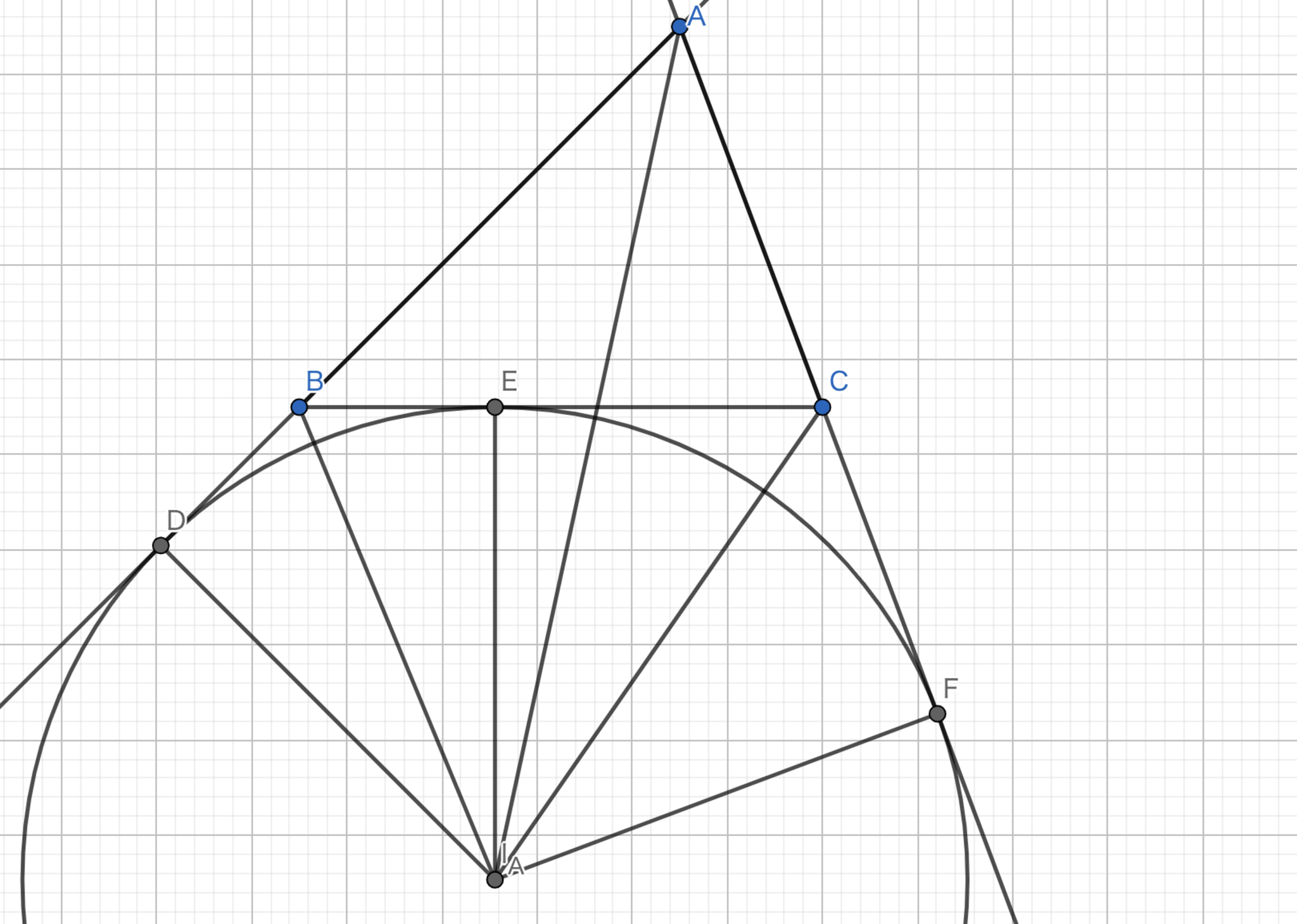
図9.傍接円の半径

方針：内接円の半径と同様に面積についての式を立てる。

　\(|AB|=c,|BC|=a,|CA|=b,|I_{A}E|=r_{A}\) とすると、面積 \(S\) について、以下の式が成り立つ。 \(S = \triangle ABI_{A} + \triangle ACI_{A} - \triangle BCI_{A} = \frac{cr_{A}}{2} + \frac{br_{A}}{2} - \frac{ar_{A}}{2} = \frac{1}{2}r_{A} \left(-a+b+c\right)\) が得られる。これを \(r_{A}\) について解くと \(r_{A} = \frac{2S}{-a+b+c}\) が得られる。 最右辺に関しては内接円と同じように、\(S\) をヘロンの公式を用いて \(a,b,c\) のみで表すことで得られる。 \(\blacksquare\)

証明

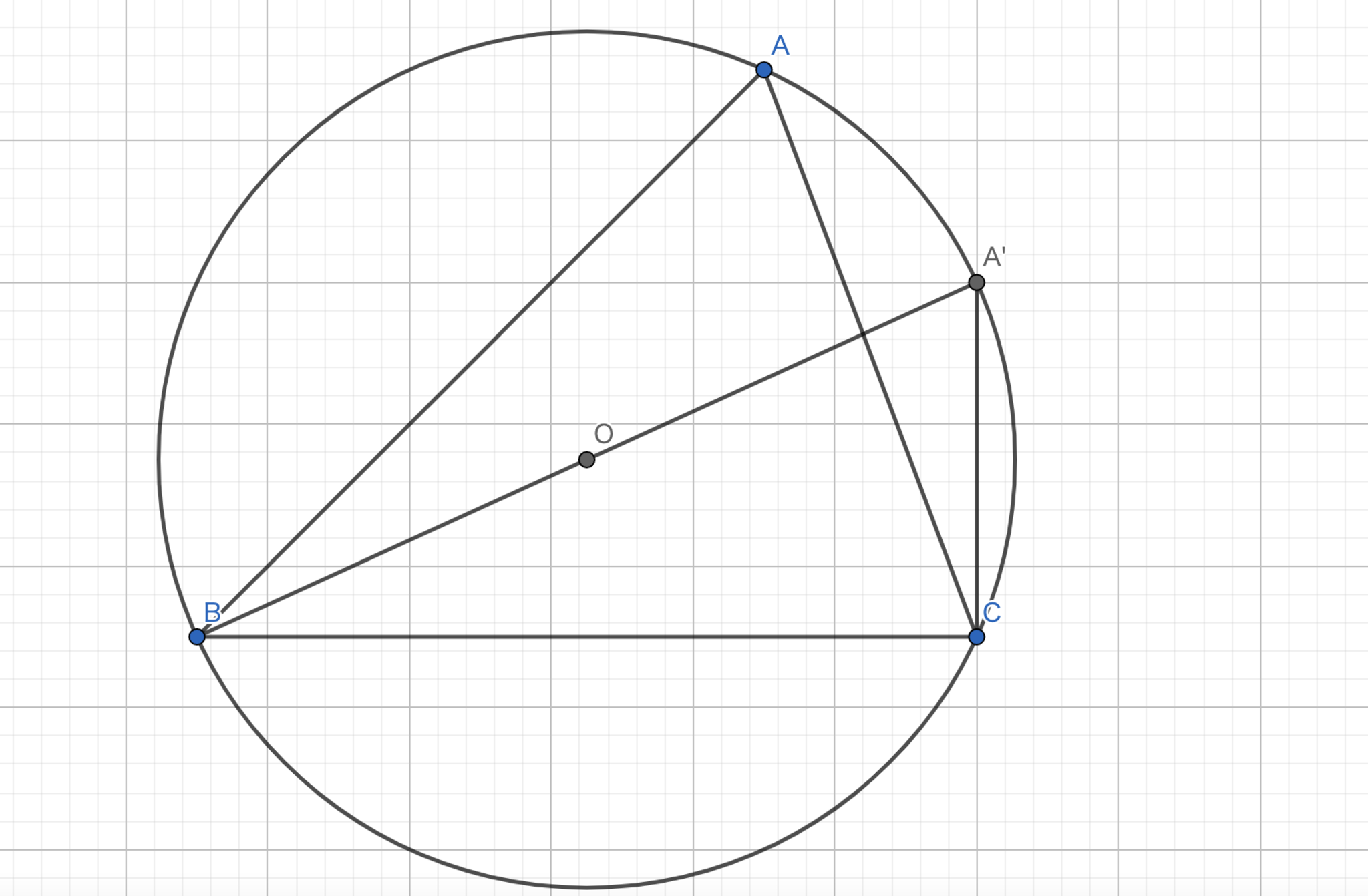
図10.外接円の半径

図のように \(A'\) をとる。 円周角の定理より、\(\angle BAC\) = \(\angle BA'C\) である。また、\(2R\sin\angle BA'C = 2R\sin\angle BAC\) = \(a\) であるから、これを \(R\) について解くことで \(R = \frac{a}{2\sin A}\) が得られる。同様に、\(R = \frac{a}{2\sin A} = \frac{b}{2\sin B} = \frac{c}{2\sin C}\) が得られる。 \(S = \frac{1}{2}bc\sin A\) であるので、\(\sin A = \frac{2S}{bc}\) が得られる。これを \(R = \frac{a}{2\sin A}\) に代入すると、\(\frac{a}{2\frac{2S}{bc}} = \frac{abc}{4S}\) が得られ、題意は示された。 最右辺に関しては、内接円の半径と同じように、\(S\) をヘロンの公式を用いて \(a,b,c\) のみで表すことで得られる。 \(\blacksquare\)

証明

定理6より \(\frac{1}{r} = \frac{a+b+c}{2S}\)、定理7より \(\frac{1}{r_{A}} = \frac{-a+b+c}{2S}\)、\(\frac{1}{r_{B}} = \frac{a-b+c}{2S}\)、\(\frac{1}{r_{C}} = \frac{a+b-c}{2S}\) である。 \[ \begin{align*} \frac{1}{r_{A}} + \frac{1}{r_{B}} + \frac{1}{r_{C}} & = \frac{\left(-a+b+c\right) + \left(a-b+c\right) + \left(a+b-c\right)}{2S} \\ & = \frac{a+b+c}{2S} \\ & = \frac{1}{r} \end{align*} \] よって、題意は示された。 \(\blacksquare\)

証明

定理6より \(r = \frac{2S}{a+b+c}\)、定理7より \(r_{A} = \frac{2S}{-a+b+c}\)、\(r_{B} = \frac{2S}{a-b+c}\)、\(r_{C} = \frac{2S}{a+b-c}\) である。 \[ \begin{align*} \sqrt{rr_{A}r_{B}r_{C}} & = \sqrt{\frac{2S}{a+b+c} \cdot \frac{2S}{-a+b+c} \cdot \frac{2S}{a-b+c} \cdot \frac{2S}{a+b-c}} \\ & = \sqrt{\frac{16S^{4}}{16S^{2}}} \\ & = S \end{align*} \] よって、題意は示された。 \(\blacksquare\)

証明

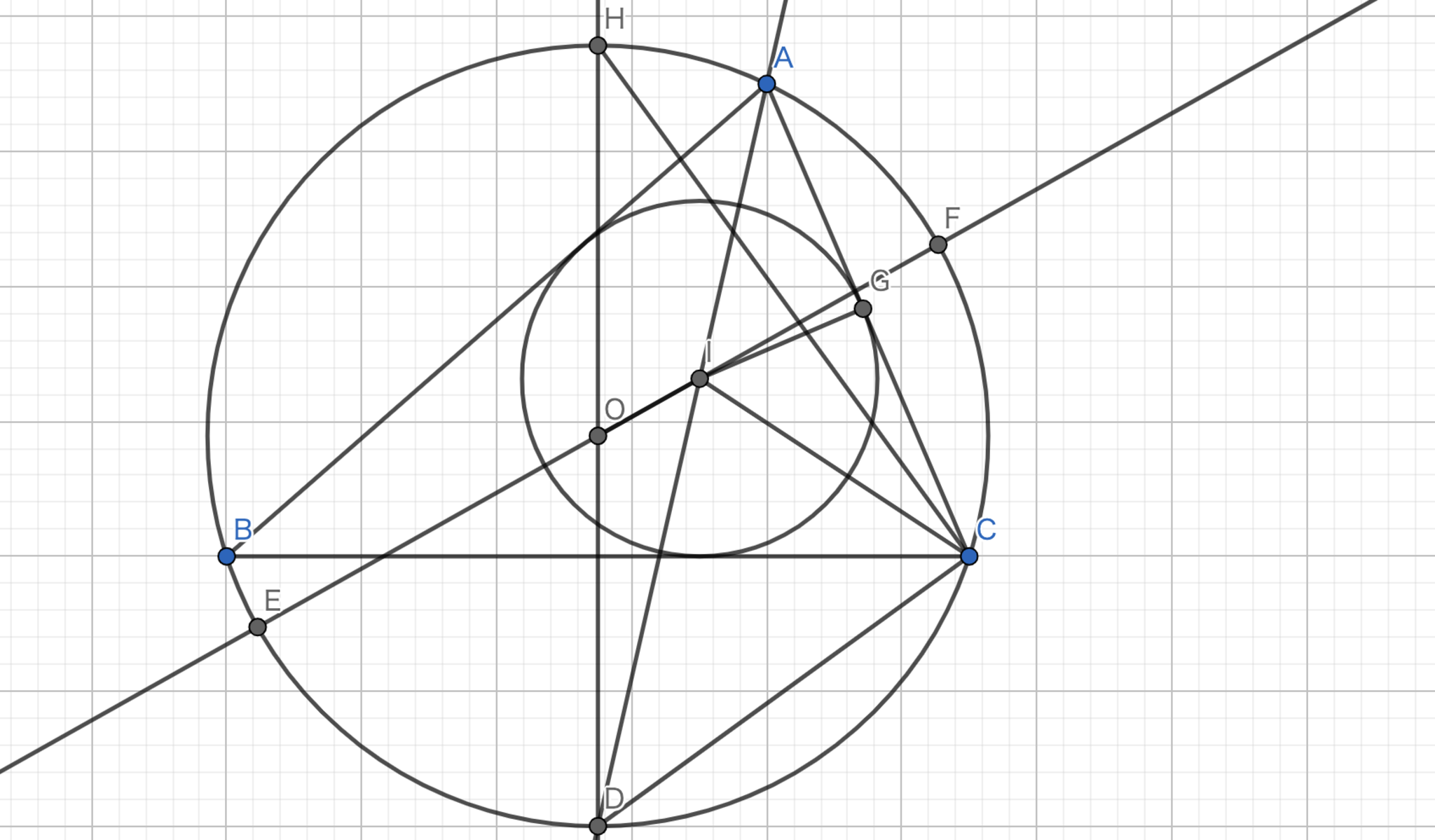
図11.オイラーの公式

方針: 方べきの定理を使用する。

　\(d^{2}=R^{2}-2Rr \Longleftrightarrow (R+d)(R-d)=2Rr\) である。 \(R+d\) は \(IE\) を表していて、 \(R-d\) は \(IF\) を表している。 方べきの定理より、\((R+d)(R-d)=|FI|\cdot |IE|=|AI|\cdot |ID|\) である。

　\(\angle{BCD} = α\) とおくと、円周角の定理より、\(\angle{BAD} = α\) となり、角の二等分線より、\(\angle{CAD} = α\) も従う。\(\angle{ACI}=β\) とすると、角の二等分線より \(\angle{BCI}=β\) である。ここで、\(\angle{ICD} = α+β\) であり、\(\angle{CID} = α+β\) であるから、三角形 \(DIC\) は二等辺三角形である。これより、\(AI \cdot ID\) = \(AI \cdot CD\) である。

　三角形 \(CDH\) と三角形 \(GIA\) はそれぞれ直角三角形であり、\(\angle{DHC} =\angle{IAG} = α\) であるから相似である。ここで三角形 \(AGI\) と三角形 \(HCD\) の相似比を \(1:k\) とすると、\(AI \cdot CD\) = \(AI \cdot GI \cdot k\) となる。また、\(AI \cdot GI \cdot k\) = \(HD \cdot GI\) である。\(HD\) = \(R\)、 \(GI\) = \(r\) であるから、\(d^{2}=R^{2}-2Rr\) である。 よって、題意は示された。\(\blacksquare\)

五心の関係性

中点三角形とは、三角形の各辺の中点を結んだ三角形です。

証明

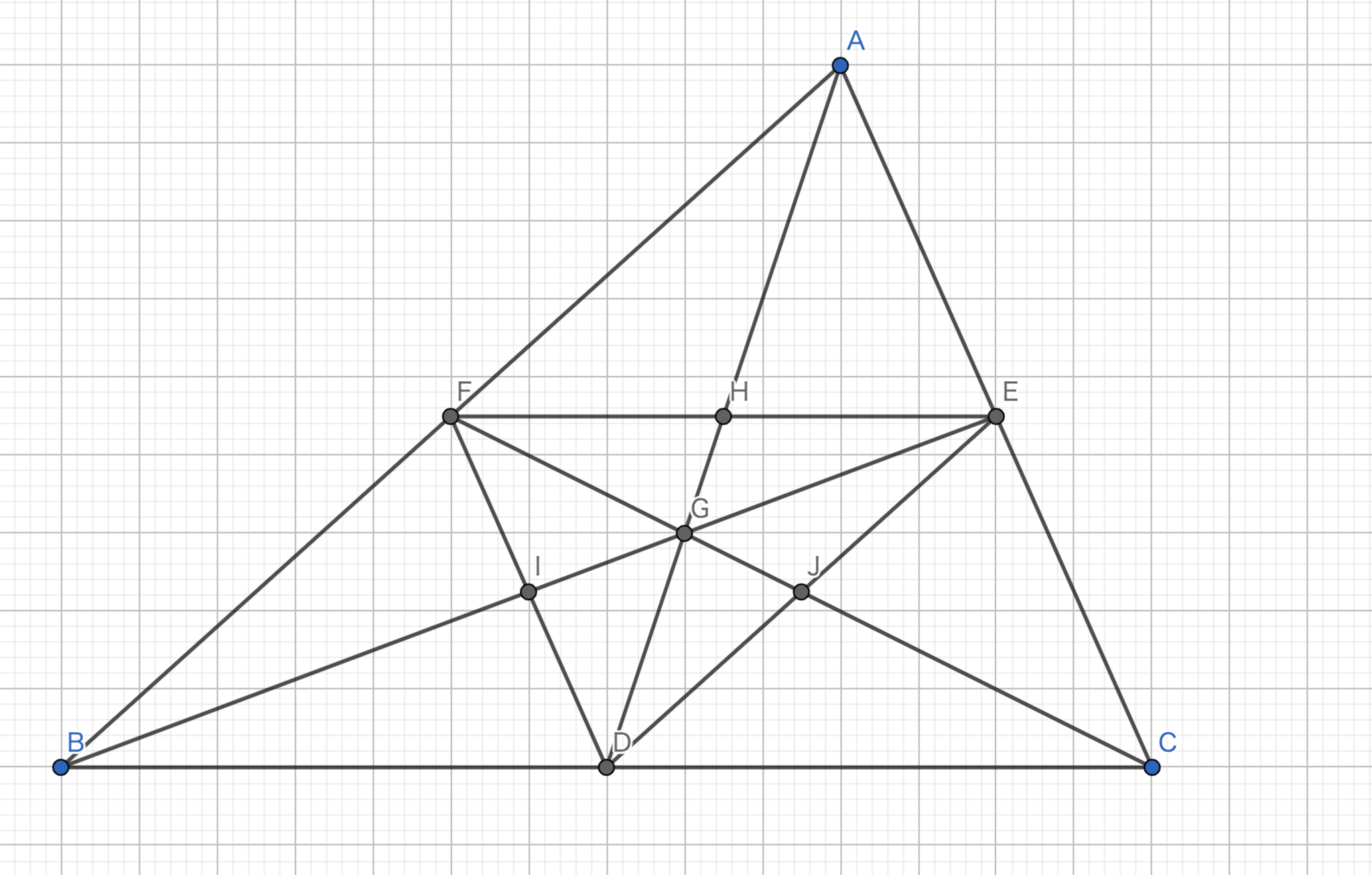
図12.中点三角形の重心

中点連結定理より、\(H\)は\(EF\)の中点である。また、\(AD\)は\(H\)を通る。同様に、\(BE\)は\(I\)を、\(CF\)は\(J\)を通る。よって、\(G\)は元の三角形の重心である。\(\blacksquare\)

証明

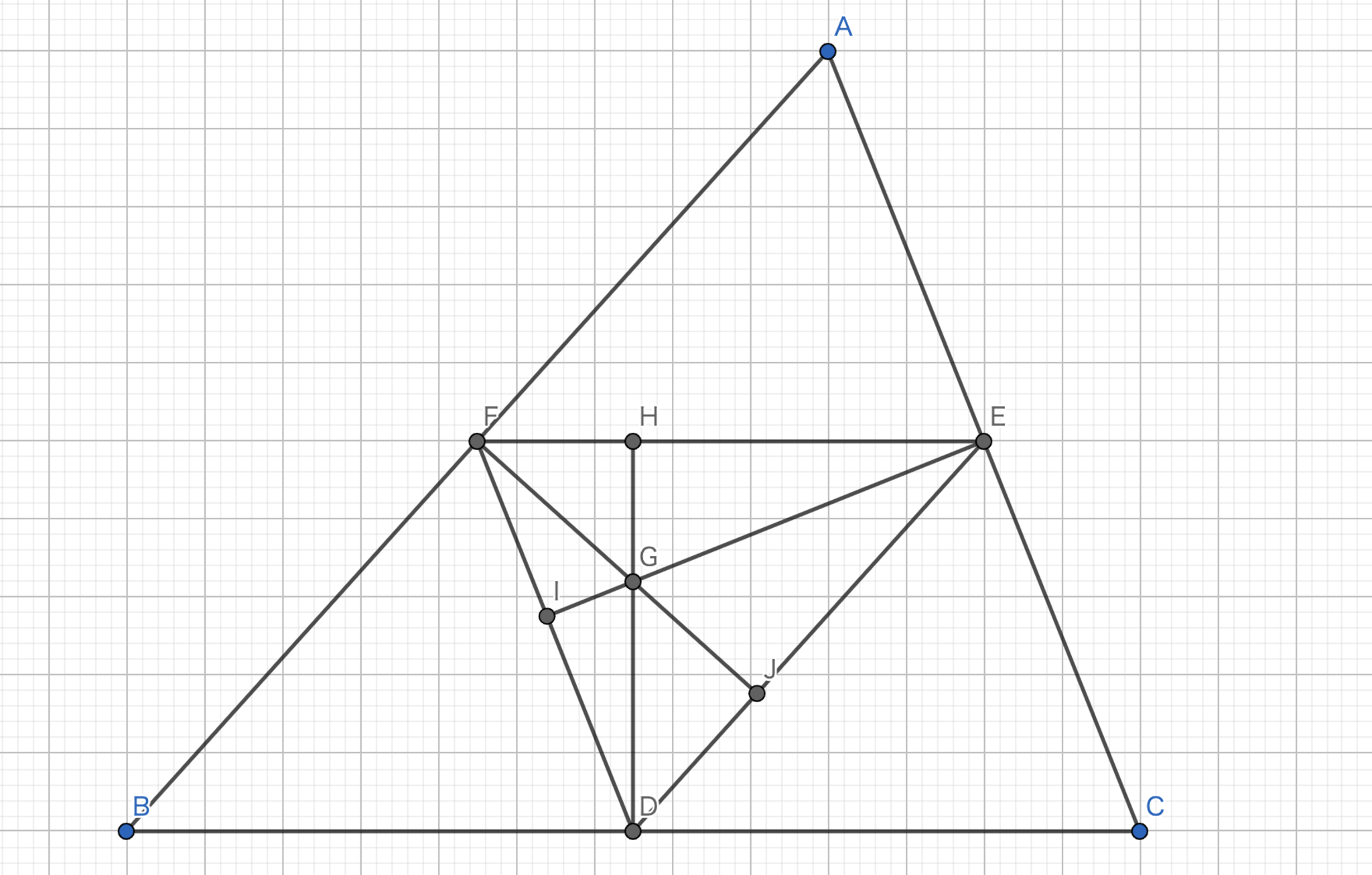
図13.中点三角形の垂心

中点連結定理より、\(EF\) が \(BC\) に平行であるから、\(DH\) は \(BC\) に垂直である。\(DH\) は \(BC\) に垂直であり、中点を通るから垂直二等分線である。同様に、\(EI\)、\(FJ\) も垂直二等分線である。故に、\(G\) は元の三角形の外心である。\(\blacksquare\)

垂足三角形とは、各頂点から対辺への垂線の足を結んだ三角形です。

証明

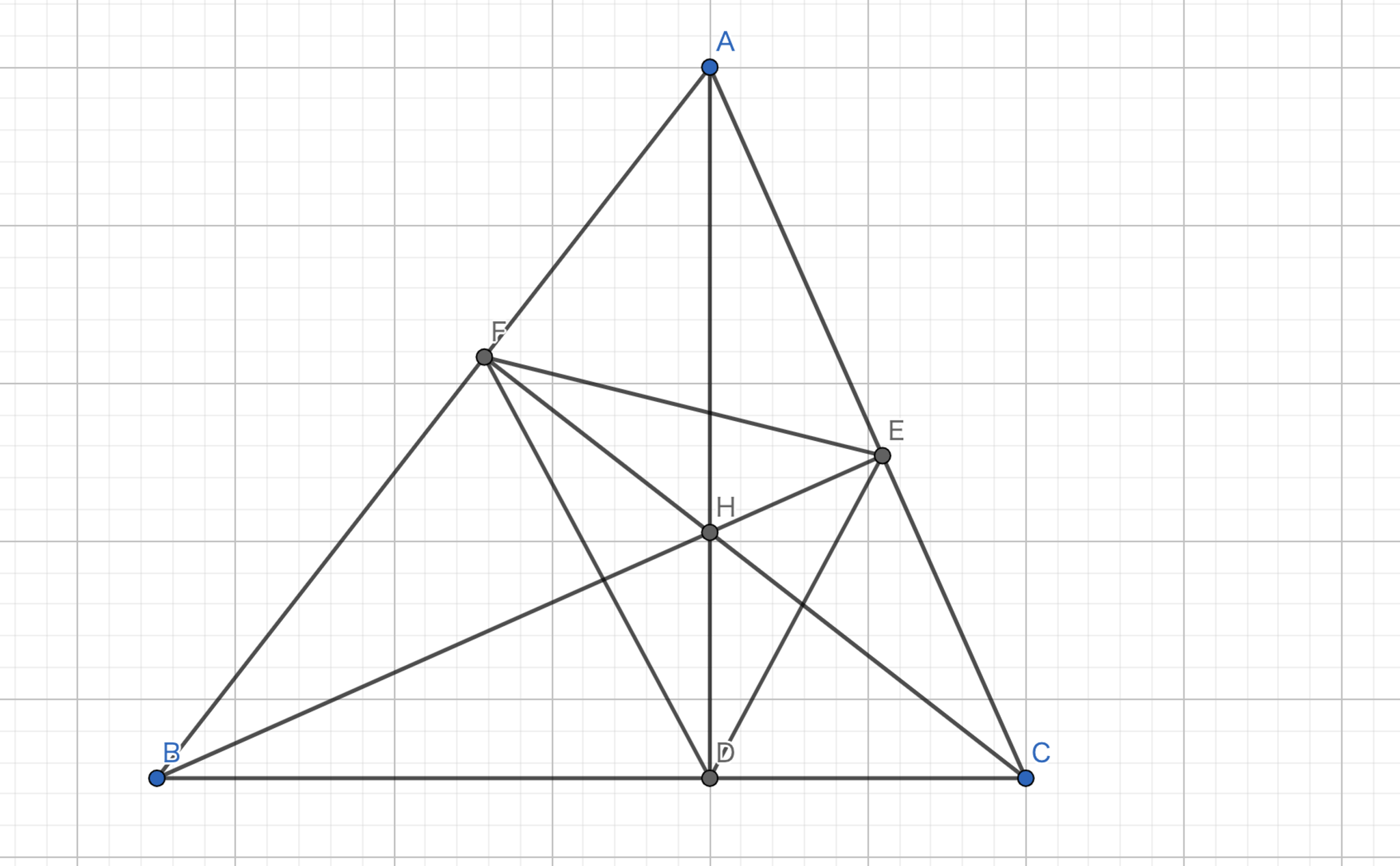
図14.垂足三角形の内心

方針: 元の三角形の垂心が垂足三角形の内心であることを示す。共円を利用して、簡単な角度計算で示す。

　\(\angle{ABC} = x\) とする。四角形\(AFHE\)は共円であるから、\(\angle {FEH} = x\) である。また、四角形\(FBCE\)も共円であるから、\(\angle {FCB} = x\) である。さらに、四角形\(CEHD\)も共円であるので \(\angle {DEH} = x\) である。故に、\(EB\) は \(\angle FED\) の角の二等分線である。同様に、\(FC, DA\) も角の二等分線であるから \(H\) は垂足三角形の内心である。故に題意は示された。 \(\blacksquare\)

証明

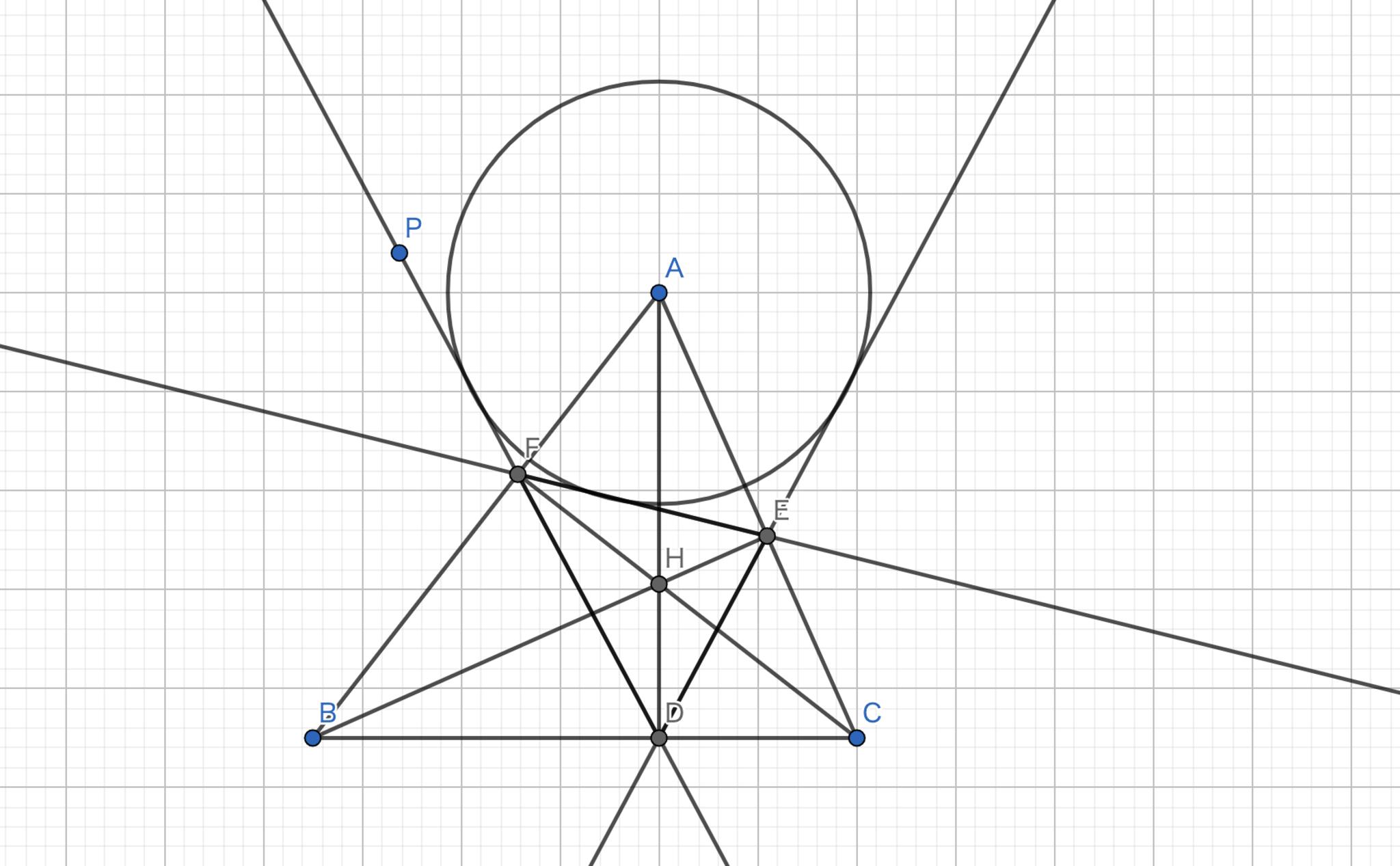
図15.垂足三角形の傍心

定理14の証明と同様に、\(\angle EFH = \angle DFG\) である。また、\(\angle AFE = 90° - \angle EFH\)、\(\angle BFD = 90° - \angle DFH\) であるから、\(\angle AFE = \angle BFD\) である。また、対頂角より \(\angle PFE = \angle DFB\) であるから、\(\angle PFA = \angle EFA\) である。点 \(E\) に関しても同様。従って、\(A\) は点 \(D\) に関する三角形 \(DEF\) の傍心である。 \(\blacksquare\)

証明

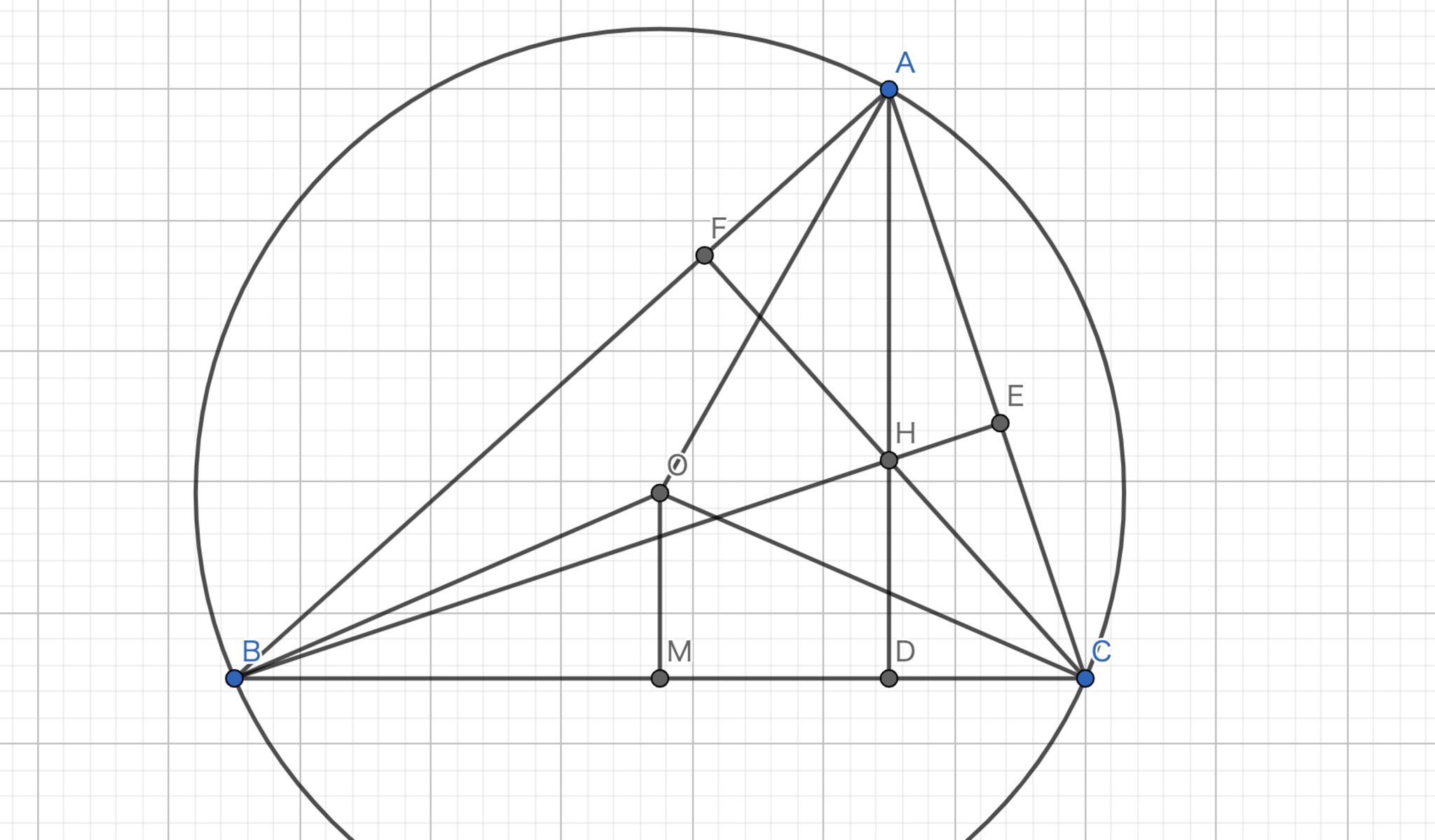
図16.垂足三角形の傍心

三角形\(OMB\)と三角形\(OMC\)は合同であるので\(\angle {BOM} = \angle {COM}\)である。また、円周角の定理より\(2\angle{BAC} = \angle {BOC}\)である。故に、\(\angle {BOM} = \angle {COM} = \angle{BAC}\)である。これを\(α\)とする。\(\angle{OCB} = 90°-α\)である。\(\angle {FCA} = 90°-α\)である。故に\(\angle{ACF} = \angle{BCO}\)である。残りの頂点も同様のことが言えるから垂心は外心の等角共役点である。 \(\blacksquare\)

五心関連の定理

証明

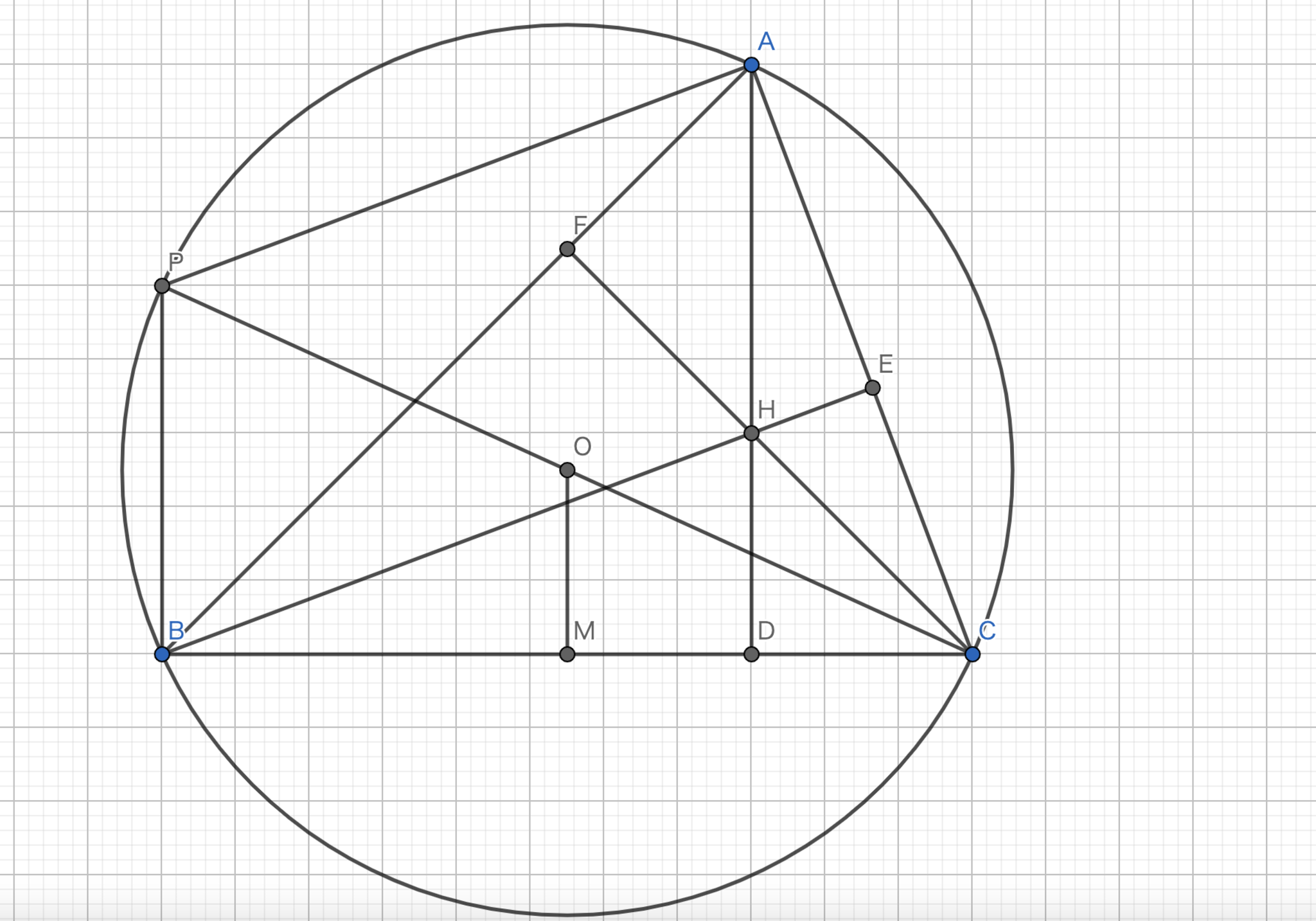
図12.オイラー線1

直線\(CO\)と円との交点を\(P\)とする。この時、\(CP\)は円の直径である。また、\(BC\)の中点を\(M\)とすると、中点連結定理より、\(OM\) は \(PB\) に平行であり、\(2|OM|=|PB|\)である。\(AD \perp BC\)、\(PB \perp BC\) であるから、\(AD \parallel PB\) である。また、垂心の性質と円周角の定理より、\(BE \perp AC\)、\(PA \perp AC\) であるから、\(BE \parallel PA\) である。よって、四角形\(PBHA\)は平行四辺形である。よって、\( |AH| = |PB| = 2|OM| \)。

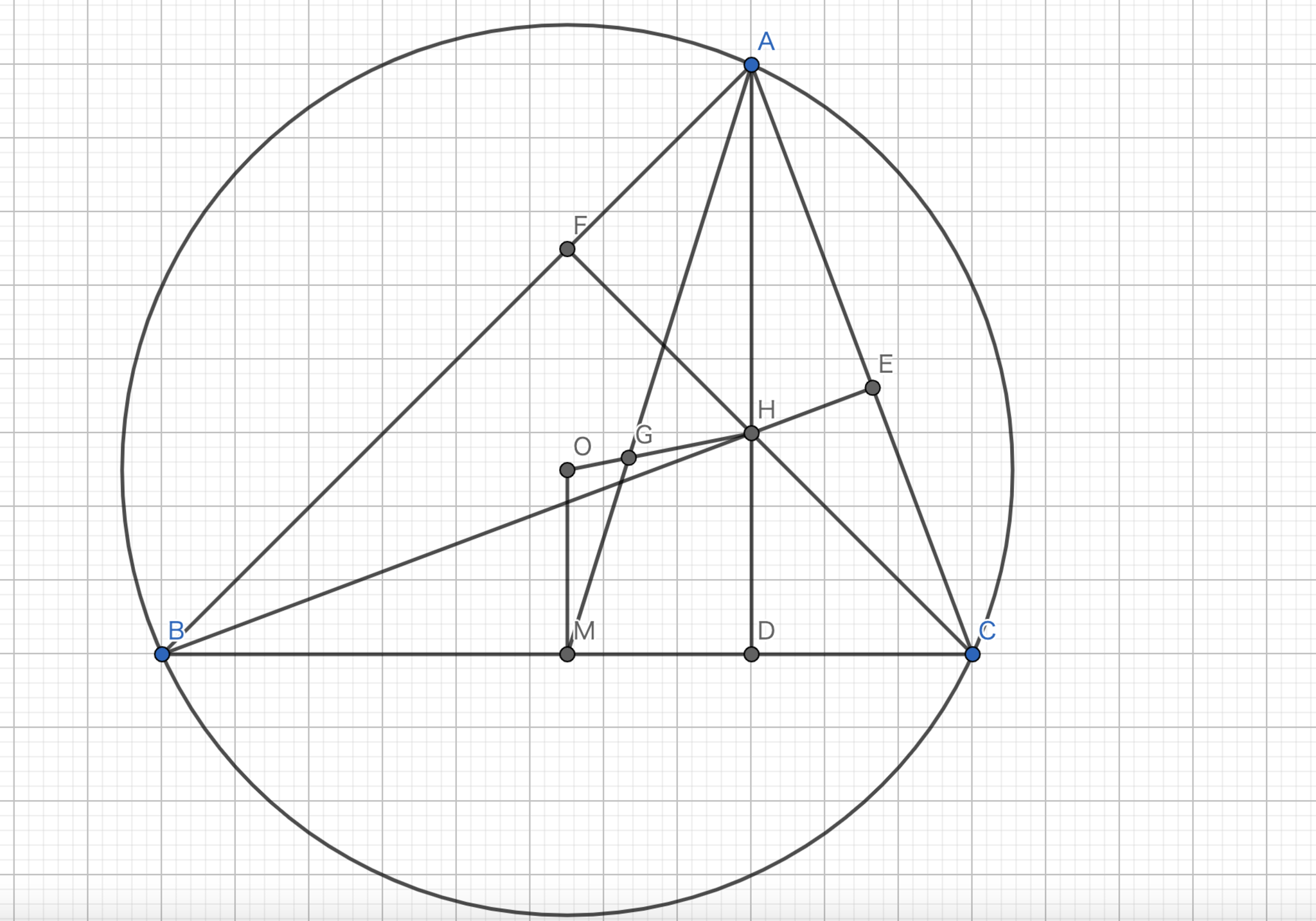
図13.オイラー線2

証明

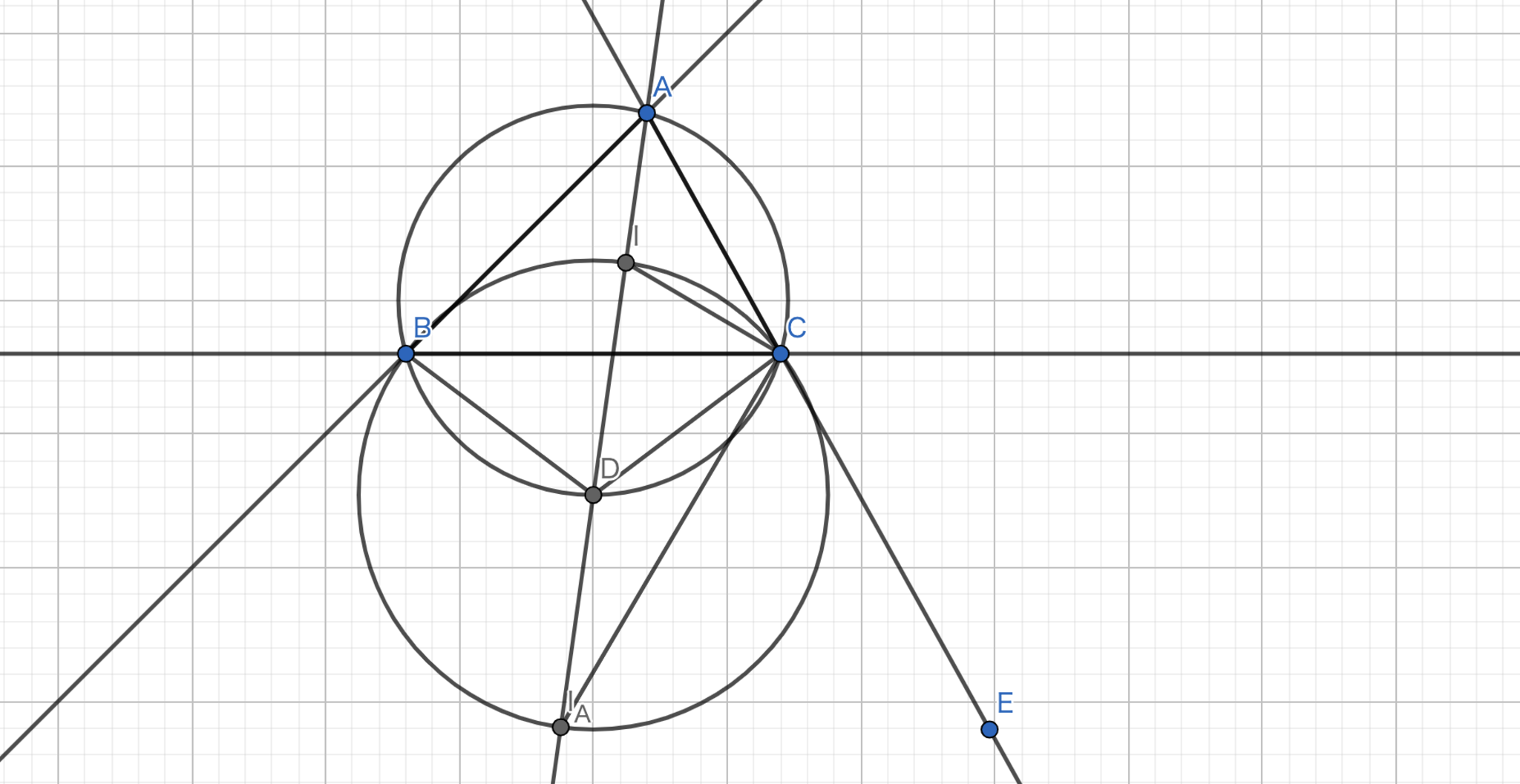
図14.トリリウムの定理

方針: \(|ID| = |BD| = |I_{A}D| = |CD|\) となることを示す。

　円周角の定理より、\(\angle{DBC} = \angle{DCB}\) であるから \(|DB| = |DC|\) である。また、\(\angle{CID} = \angle{CAI} + \angle{ICA} = \angle{BAD} + \angle{ICB} = \angle{BCD} + \angle{ICB} = \angle{ICD}\) であるので \(|DI| = |DC|\) である。このことから、三点 \(B, I, C\) は \(D\) を中心とする共円である。よって、ここでは \(\angle{ICI_{A}} = 90°\) であることを示せば十分である。\(\angle{DCI_{A}} = x\) とすれば、傍心の性質より \(\angle{I_{A}CE} = x + \angle{BCD}\) となる。ここで、\(\angle{ACE} = 2\angle{ICB} + 2(\angle{BCI_{A}}) = 180°\) であることから、\(\angle{ICI_{A}} = \angle{ICB} + (\angle{BCI_{A}}) = 90°\) が得られる。よって、円周角の定理の逆より、\(II_{A}\) は直径であり、\(D\) が中心であるので、\(|ID| = |BD| = |I_{A}D| = |CD|\) である。 \(\blacksquare\)

証明

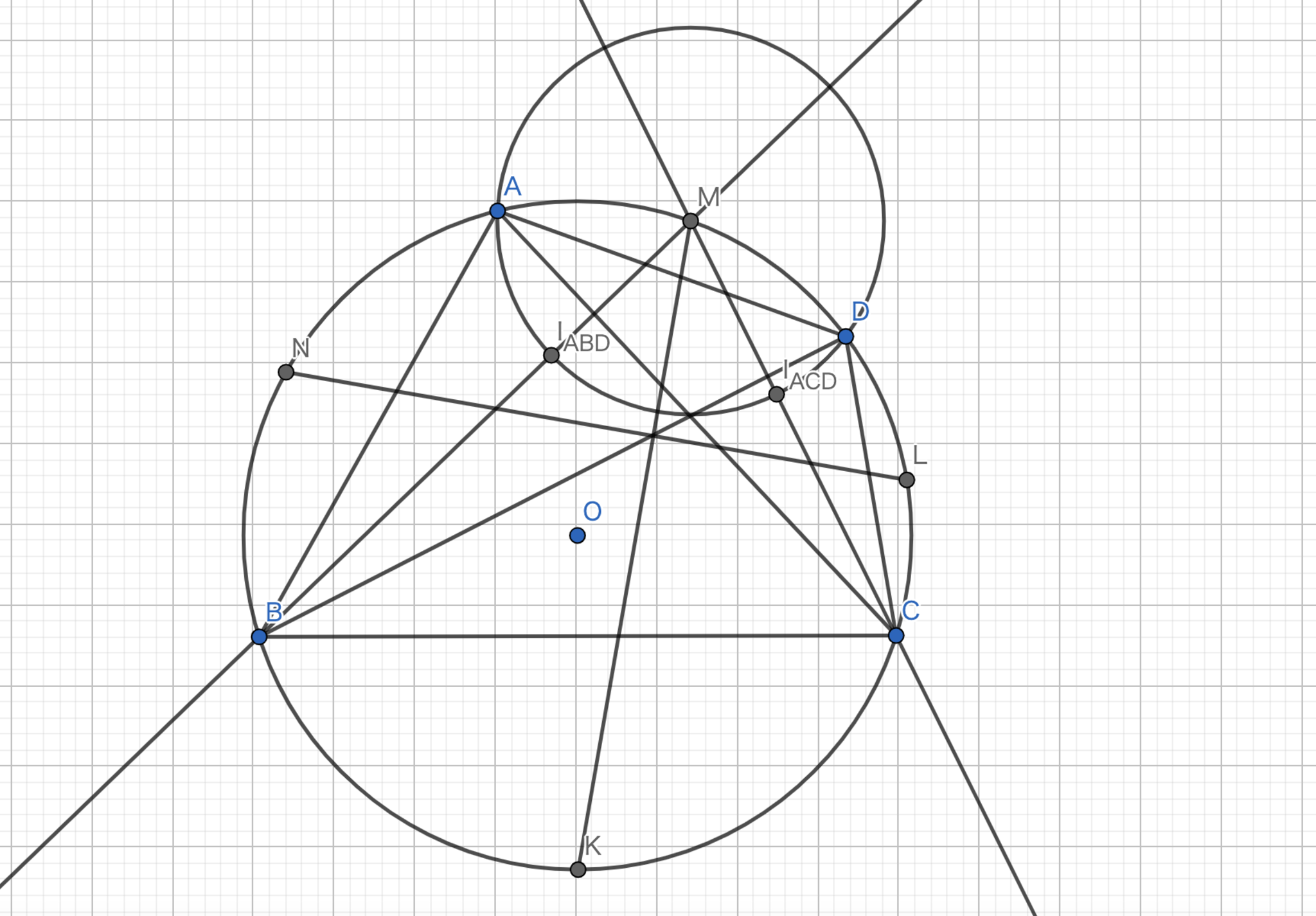
図15.丸山良寛の定理

方針：内心と外接円がたくさん登場していることからトリリウムの定理を利用する。

　弧 \(AB, BC, CD, DA\) の中点を \(N, K, L, M\) とする。 円周角の定理より、\(\angle NMK + \angle MNL = 90°\) であるから、\(MK \perp NL\) である。 ここで、トリリウムの定理より \(|MI_{ABD}| = |MI_{ACD}|\) である。 また円周角の定理より、\(\angle BMK = \angle CMK\) であるから、\(MK \perp I_{ABD}I_{ACD}\) である。 よって、\(I_{ABD}I_{ACD} \parallel NL\) である。 同様に内心を \(I_{ABC}, I_{BCD}\) と定めれば、\(I_{ABD}I_{ABC} \parallel MK, I_{ABC}I_{BCD} \parallel NL, I_{BCD}I_{ACD} \parallel MK\) であるから、四角形 \(I_{ABD}I_{ABC}I_{BCD}I_{ACD}\) は長方形である。 ここで、\(I_{ABD}I_{BCD}\) と \(I_{ABC}I_{ACD}\) の交点を \(X\) とすると、\(I_{ABD}X = I_{ABC}X = I_{BCD}X = I_{ACD}X\) となる。 またこの長さを \(x\) とする。三角形 \(OI_{ABD}I_{BCD}\) で中線定理を用いると、\(OI_{ABD}^2 + OI_{BCD}^2 = 2(OX^2 + x^2)\) となる。 同様に、三角形 \(OI_{ABC}I_{CDA}\) についても中線定理を適用すると、\(OI_{ABC}^2 + OI_{CDA}^2 = 2(OX^2 + x^2)\) となる。 このことから、\(OI_{ABD}^2 + OI_{BCD}^2 = OI_{ABC}^2 + OI_{CDA}^2\) が得られる。 ここで、オイラーの定理を用いて、\(d^2 = R^2 - 2Rr\) をそれぞれ代入する。 全て同様の円に内接するので外接円の半径 \(R\) は等しい。 従って \(R^2 - 2Rr_1 + R^2 - 2Rr_3 = R^2 - 2Rr_2 + R^2 - 2Rr_4\) が得られる。 よって、\(r_{1} + r_{3} = r_{2} + r_{4}\) である。 \(\blacksquare\)

これと帰納法を組み合わせれば、日本の定理が得られるらしいです。おもしろい。

この中心は、九点円の中心の等角共役点らしいです。 本記事の元記事を書いた時点では、初等的証明を思いつくことができなかったので複素座標を用いて証明しました。 元記事を投稿してすぐに翁さんが初等的証明を投稿してくださいました。 とても面白いので、ぜひご覧ください。 せっかくなので今回は複素座標を用いてみます。

証明

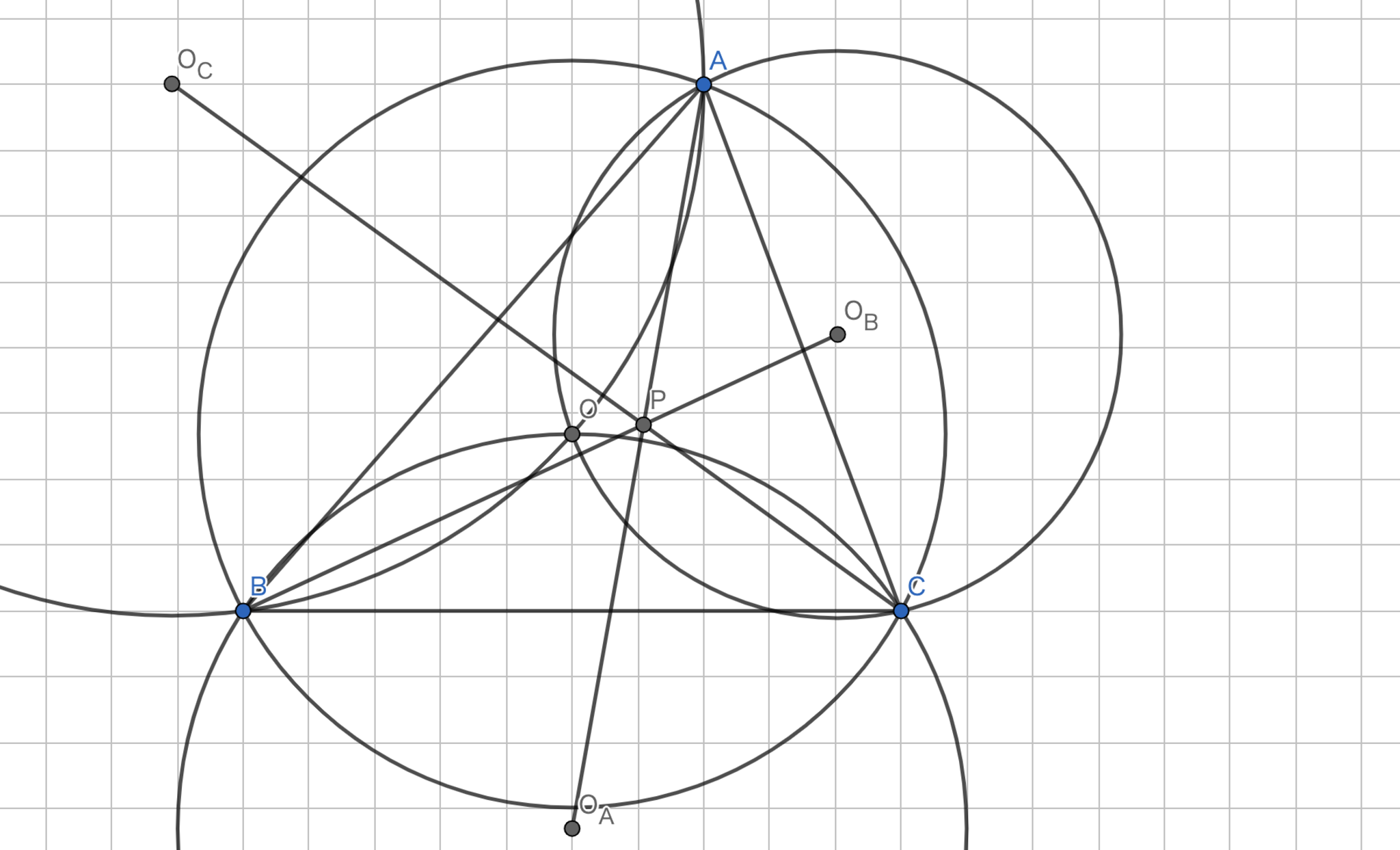
図16.コスニタの定理

方針: 初等的に示すのは難しそうなので複素を利用する。

　\(\displaystyle A(a), B(b), C(c), O(0)\) として、三角形\(ABC\)の外接円を\(|z|=1\) とする。\(O_{A}\) が\(OB\)の垂直二等分線と\(OC\)の垂直二等分線の交点であることを利用して \(O_{A}\) を求めていく。\(OA, OB, OC\) の垂直二等分線の式はそれぞれ以下のようになる。 \[ OA: z + a^2\bar{z} = a \\ OB: z + b^2\bar{z} = b \\ OC: z + c^2\bar{z} = c \] \(OA\) が再び円と交わるのは \(P(\frac{ab+ac-bc}{a-b-c})\) である。同様に、\(OB\) では \(Q(\frac{ab+bc-ac}{-a+b-c})\)、\(OC\) は \(R(\frac{ac+bc-ab}{-a-b+c})\) である。ここで、後述する補題より \[ \begin{aligned} &\left(P-b\right)\left(Q-c\right)\left(R-a\right)+\left(c-P\right)\left(a-Q\right)\left(b-R\right) = 0 \end{aligned} \] であることを示せばよい。 \[ \begin{align*} \left(P-b\right)\left(Q-c\right)\left(R-a\right)+\left(c-P\right)\left(a-Q\right)\left(b-R\right) & = \frac{b^{2}+ca}{a-b-c}\cdot\frac{c^{2}+ab}{-a+b-c}\cdot\frac{a^{2}+bc}{-a-b+c} \\ & +\frac{-c^{2}-ab}{a-b-c}\cdot\frac{-a^{2}-bc}{-a+b-c}\cdot\frac{-b^{2}+ca}{-a-b+c} \\ & = \frac{\left(b^{2}+ca\right)\left(c^{2}+ab\right)\left(a^{2}+bc\right)-\left(a^{2}+bc\right)\left(b^{2}+ca\right)\left(c^{2}+ab\right)}{\left(a-b-c\right)\left(-a+b-c\right)\left(-a-b+C\right)} \\ & = 0 \end{align*} \] よって題意は示された。 \(\blacksquare\)

証明

\(\Longrightarrow\) の証明

(i) 三本が平行である場合

直線 \(ad, be, cf\) はそれぞれ以下のように表される。 \[ z + ad\overline{z} = a + d \\ z + be\overline{z} = b + e \\ z + cf\overline{z} = c + f \] このとき、全て平行であるから、\(ad = be = cf\) である。\(ad = be = cf = x\) とすれば、 \[ \begin{align*} &(a - b)(c - d)(e - f) + (f - a)(b - c)(d - e) \\ &= -abd + abe + acd - acf - ade + adf - bce + bcf + bde - bef - \operatorname{cdf} + cef \\ &= -bx + ax + cx - ax - ex + fx - cx + bx + dx - fx - dx + ex \\ &= 0 \end{align*} \] となって、成立する。

(ii) 三本が一点で交わる場合

\[ z + ad\overline{z} = a + d \\ z + be\overline{z} = b + e \\ z + cf\overline{z} = c + f \] であり、これは全て同じ点 \(w\) を通るので、 \[ a + d - ad\overline{w} = b + e - be\overline{w} = c + f - cf\overline{w} \] となる。一方で、\((a - b)(c - d)(e - f) + (f - a)(b - c)(d - e) = ad(c + f - b - e) + (a + d)(be - cf) - be(c + f) + cf(b + e)\) であるから、頑張って計算すると、 \[ (a - b)(c - d)(e - f) + (f - a)(b - c)(d - e) = 0 \] である。よって、成立する。

\(\Longleftarrow\) の証明

(i) 平行であることの証明

\(be, ef\) が平行であるときに \(ad\) も平行であることを示す。\(be // cf\) だから \(ad = be\) である。このことを利用して \((a - b)(c - d)(e - f) + (f - a)(b - c)(d - e)\) を整理すると、\((ad - be)(c + f - b - e)\) であるから、\((a - b)(c - d)(e - f) + (f - a)(b - c)(d - e) = 0\) より、\(ad = be, c + f = b + e\) である。\(ad = be\) の場合は \(ad // be\) である。また、\(c + f = b + e\) のときは二つの直線は一致する。よって成立する。

(ii) 一点で交わることの証明

\(be, cf\) が交わっているときに、\(ad\) も共点であることを示す。\(w\) で交わっているとすれば、 \[ \begin{align*} &(a - b)(a - d)(e - f) + (f - a)(b - c)(d - e) \\ &= ad(c + f - b - e) + (a + d)(be - cf) - be(w + cf\overline{w}) + cf(w + be\overline{w}) \\ &= (be - cf)(ad\overline{w} - a - d + w) \\ \end{align*} \] ここで、\((be - cf)(adw - a - d + w) = 0\) であって、\(be\) と \(cf\) は平行ではないので、\(ad\overline{w} - a - d + w = 0\) である。故に \(w + ad\overline{w} = a + d\) である。よって成立する。

九点円関連の定理

AoPSなどを見ていると、"NPC" などと略されることもあります。

証明

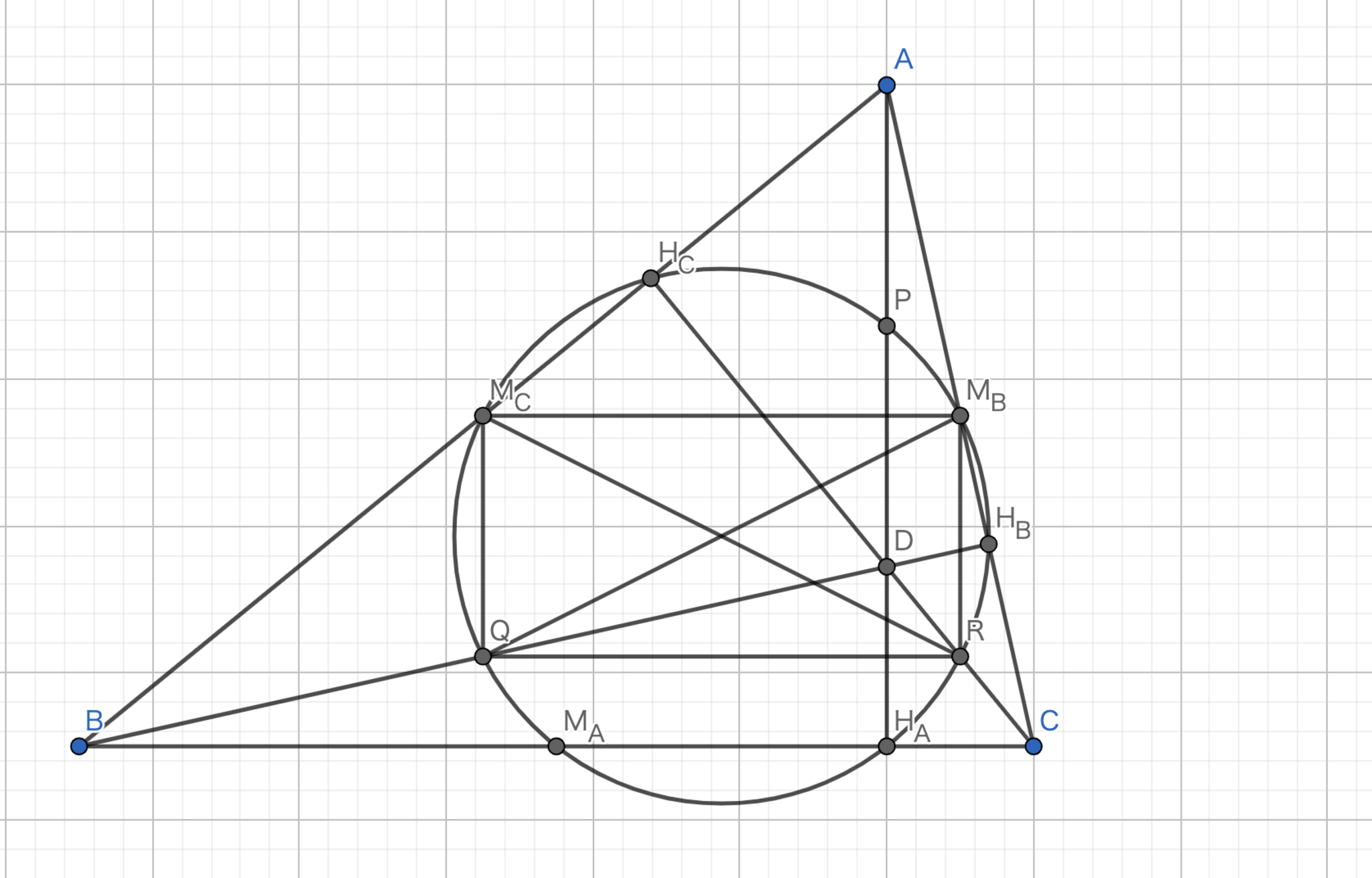
図17.九点円の存在

方針: 中点が複数存在することから中点連結定理を考える。

　三角形\(ABC\)に注目すると、中点連結定理より、\(M_{C}M_{B}\) // \(BC\)、\( |M_{C}M_{B}| = \frac{1}{2}\left|BC\right|\)がわかる。また、三角形\(DBC\)に注目すると、中点連結定理より、\(QR\) // \(BC\)、\( |QR| = \frac{1}{2}\left|BC\right|\)がわかる。このことから、四角形\(M_{C}QRM_{B}\)は長方形である。故に四点\(M_{C}QRM_{B}\)は\(M_{C}R, M_{B}Q\)を直径とする共円である。また、円周角の定理の逆より\(H_{C}, H_{B}\)も共円である。さらに、この円は三角形\(H_{B}M_{B}Q\)の外接円である。

　四角形\(M_{C}QRM_{B}\)と同様に、四角形\(M_{B}PQM_{A}\)は長方形である。さらに、円周角の定理の逆より\(H_{A}, H_{B}\)も共円である。この円は三角形\(H_{B}M_{B}Q\)の外接円であるから、先ほどの円と等しい円である。よって、九点は共円である。 \(\blacksquare\)

証明

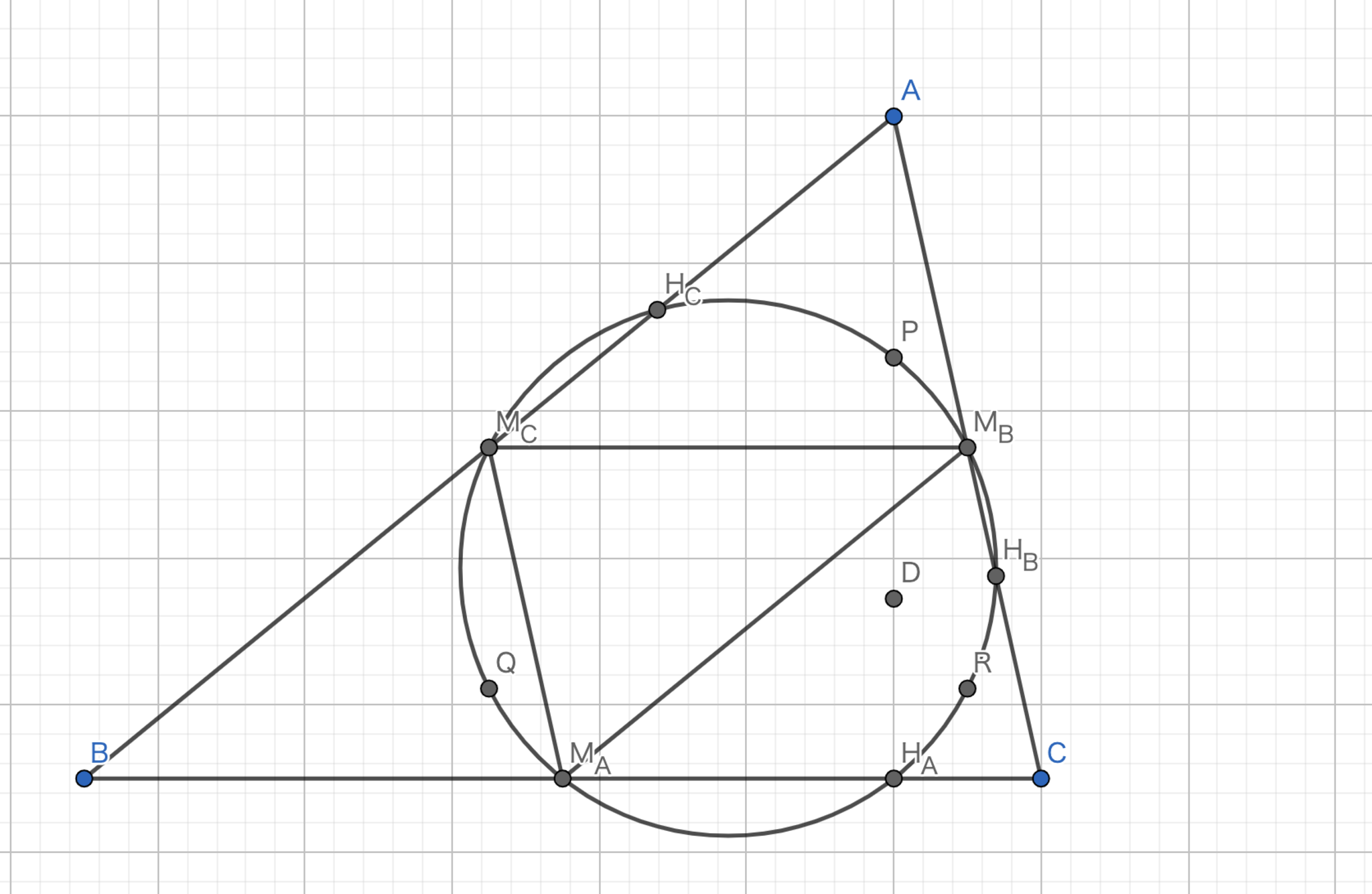
図18.九点円の半径

三角形 \(M_{A}M_{B}M_{C}\) は三角形 \(ABC\) と相似でありその比は \(1:2\) であるから外接円の半径も \(1:2\) である。九点円は三角形 \(M_{A}M_{B}M_{C}\) の外接円であるから題意は示された。 \(\blacksquare\)

証明

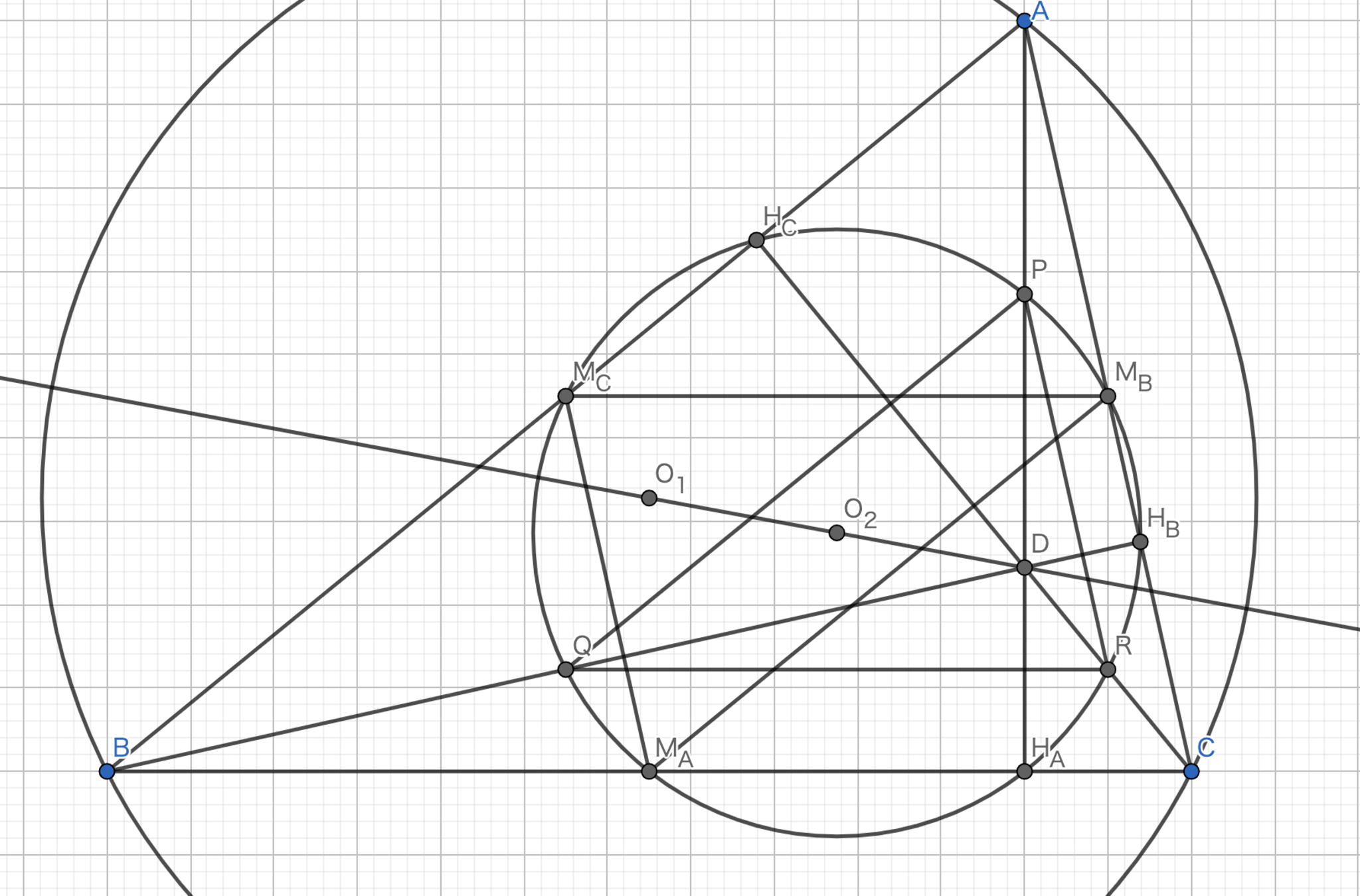
図19.九点円とオイラー線

方針: 回転相似を利用する。

　三角形 \(PQR\) は垂心 \(D\) を中心として \(0°\) 回転させて \(\frac{1}{2}\) の相似比で拡大させたものである。 また、\(PQR\) の外接円は九点円である。三角形 \(M_{A}M_{B}M_{C}\) は外心 \(O\) を中心として \(180°\) 回転させて \(\frac{1}{2}\) の相似比で拡大させたものである。 また、三角形 \(M_{A}M_{B}M_{C}\) の外接円は九点円である。 後述する定理16より、中点三角形の垂心は元の三角形の外心であるから\(O_{1}\) と \(D\) は共に垂心である。 さらに、これらの二つの三角形は九点円を共有して \(180°\) 回転した合同であるから \(O_{1}\) と \(D\) は \(O_{2}\) を中心とする対称な点である。 よって、九点円の中心は外心と垂心の中心である。 \(\blacksquare\)

演習問題

今回は、易しめの基本的な問題を紹介していきます。本格的な競技数学向けの問題は、各心の解説記事のほうで扱います。

視点を変えてみましょう。

内心で成り立つことは、傍心でも成り立ちます。

図20.トリリウムの定理-傍心版

トリリウムの定理と同様の流れで行う簡単な角度追跡により、\(\angle{I_BBI_C}=\angle{I_BCI_C}=90^{\circ}\) を得るから、四点 \(I_BCBI_C\) は共円である。 また、さらに角度追跡を行うことによって \(\angle{DI_BB}=\angle{DBI_B}, \ \angle{DI_CC}=\angle{DCI_C}\) を得る。よって、円の中心は \(D\) である。

この記事の知識がないと、難問に見えるかもしれませんね。

知識をフル活用！

参考文献

[1] 丹後：コスニタの定理 , 丹後のページ , https://kyoushien.kyokyo-u.ac.jp/tango/Kosnita100108.html#kos100108k

[2] 丸山良寛の定理 , http://sintakenoko.la.coocan.jp/Cabri/J3_75a.pdf

[3] 三角形 , wikipedia, https://ja.wikipedia.org

[4] マスオ：図形の美しい３つの定理〜逆数の和〜 , 高校数学の美しい物語 , https://manabitimes.jp/math/809

[5] マスオ：オイラーの定理（内心と外心の距離）とオイラーの不等式の証明を3通りずつ , 高校数学の美しい物語 , https://manabitimes.jp/math/580