垂心と共点
今回は、知識一発ゲーを解いていきます。それでは、よろしくお願いします。
問題
問題: 垂心と共点
三角形 \(ABC\) において、各頂点から対辺への垂線の足をそれぞれ \(D,E,F\) とする。\(BE,CF\) と \(DF,DE\) との交点をそれぞれ \(X,Y\) とするとき、\(BC,EF,XY\) が一点で交わることを示せ。
\(X,Y\) が扱いにくいですね。
解説
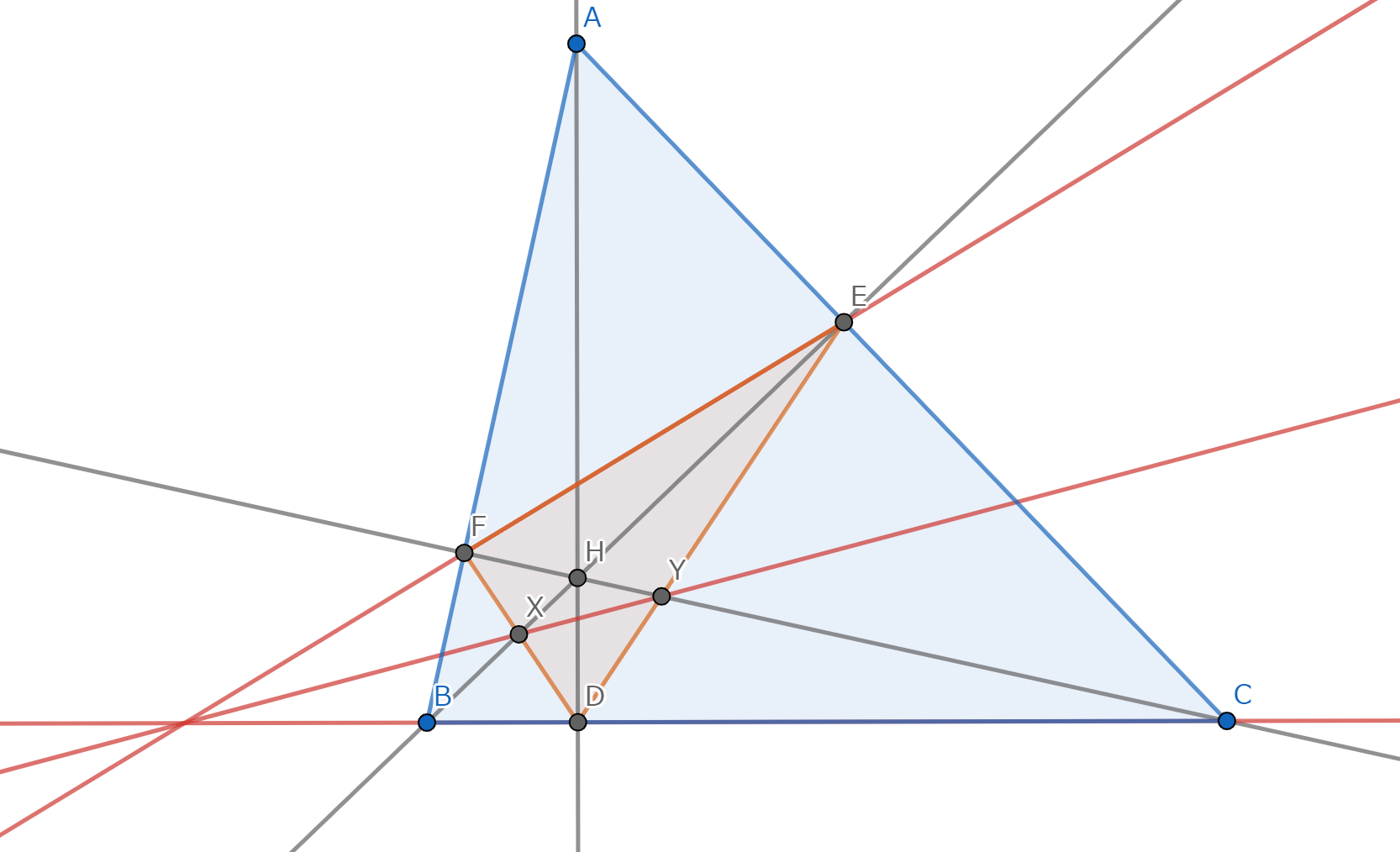
図1.解説の図形
解法1(Desarguesの定理による解法)
三角形 \(BXF,CYE\) に関するDesarguesの定理の逆より、共点が示された。
解法2(Mongeの定理による解法)
こちらの定理15より、三角形 \(DEF\) の傍心は \(A,B,C\) である。\(B,C\) を中心とする二つの傍接円と、三角形 \(DEF\) の内接円に対して、Mongeの定理を適用することによって目的の共点を得る。